Symbolic Approximations to Ricci-flat Metrics Via Extrinsic Symmetries of Calabi-Yau Hypersurfaces

Ever since Yau's non-constructive existence proof of Ricci-flat metrics on Calabi-Yau manifolds, finding their explicit construction remains a major obstacle to development of both string theory and algebraic geometry. Recent computational approaches employ machine learning to create novel neural representations for approximating these metrics, offering high accuracy but limited interpretability. In this paper, we analyse machine learning approximations to flat metrics of Fermat Calabi-Yau n-folds and some of their one-parameter deformations in three dimensions in order to discover their new properties. We formalise cases in which the flat metric has more symmetries than the underlying manifold, and prove that these symmetries imply that the flat metric admits a surprisingly compact representation for certain choices of complex structure moduli. We show that such symmetries uniquely determine the flat metric on certain loci, for which we present an analytic form. We also incorporate our theoretical results into neural networks to achieve state-of-the-art reductions in Ricci curvature for multiple Calabi-Yau manifolds. We conclude by distilling the ML models to obtain for the first time closed form expressions for Kahler metrics with near-zero scalar curvature.

cymyc -- Calabi-Yau Metrics, Yukawas, and Curvature

We introduce \texttt{cymyc}, a high-performance Python library for numerical investigation of the geometry of a large class of string compactification manifolds and their associated moduli spaces. We develop a well-defined geometric ansatz to numerically model tensor fields of arbitrary degree on a large class of Calabi-Yau manifolds. \texttt{cymyc} includes a machine learning component which incorporates this ansatz to model tensor fields of interest on these spaces by finding an approximate solution to the system of partial differential equations they should satisfy.

Calabi-Yau metrics through Grassmannian learning and Donaldson's algorithm

Motivated by recent progress in the problem of numerical K\"ahler metrics, we survey machine learning techniques in this area, discussing both advantages and drawbacks. We then revisit the algebraic ansatz pioneered by Donaldson. Inspired by his work, we present a novel approach to obtaining Ricci-flat approximations to K\"ahler metrics, applying machine learning within a `principled' framework. In particular, we use gradient descent on the Grassmannian manifold to identify an efficient subspace of sections for calculation of the metric. We combine this approach with both Donaldson's algorithm and learning on the $h$-matrix itself (the latter method being equivalent to gradient descent on the fibre bundle of Hermitian metrics on the tautological bundle over the Grassmannian). We implement our methods on the Dwork family of threefolds, commenting on the behaviour at different points in moduli space. In particular, we observe the emergence of nontrivial local minima as the moduli parameter is increased.

Learning to be Simple

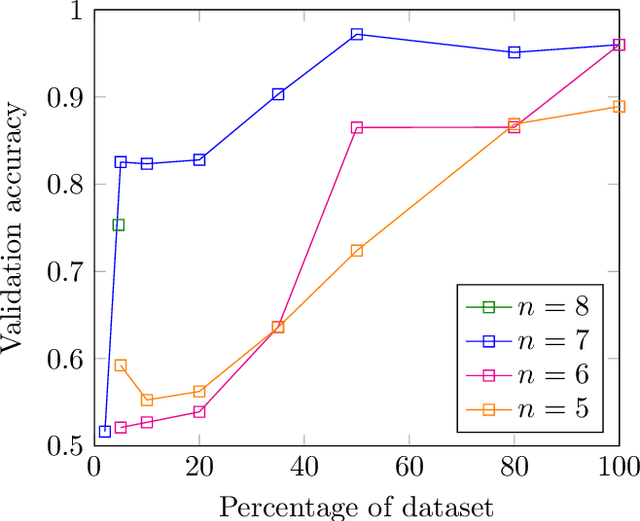
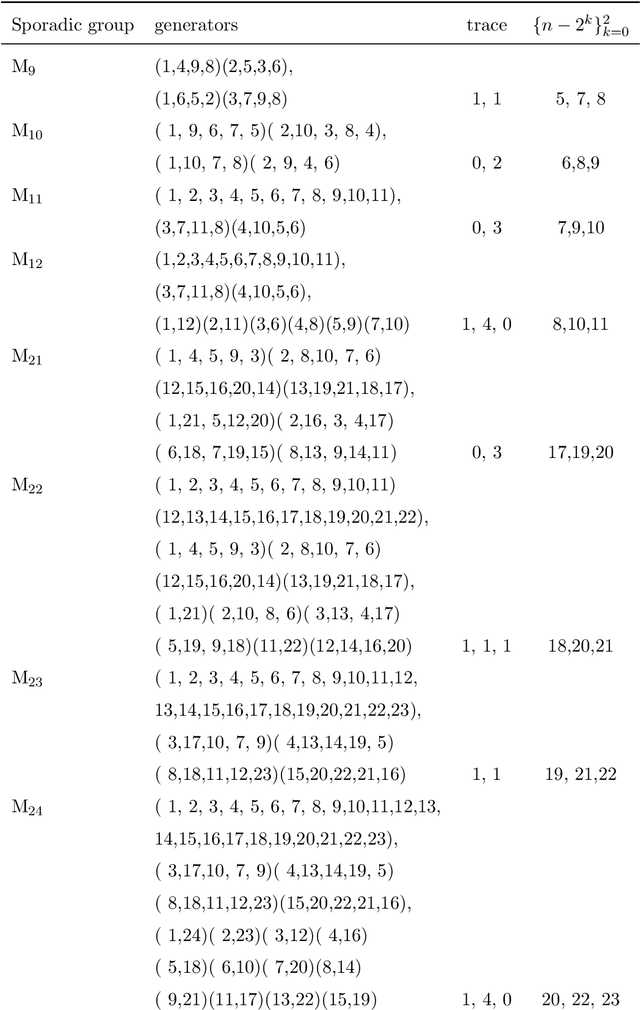
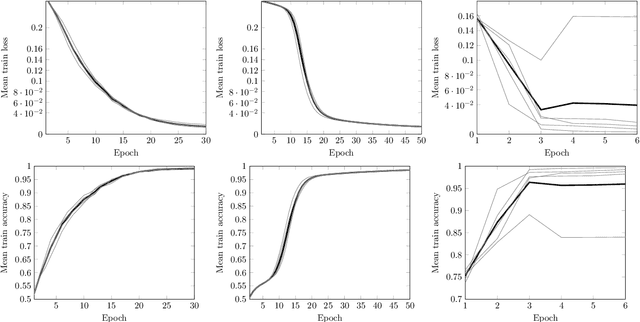
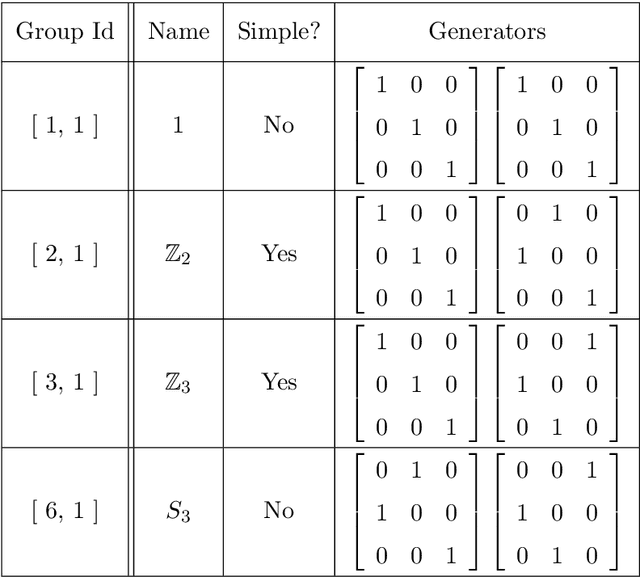
In this work we employ machine learning to understand structured mathematical data involving finite groups and derive a theorem about necessary properties of generators of finite simple groups. We create a database of all 2-generated subgroups of the symmetric group on n-objects and conduct a classification of finite simple groups among them using shallow feed-forward neural networks. We show that this neural network classifier can decipher the property of simplicity with varying accuracies depending on the features. Our neural network model leads to a natural conjecture concerning the generators of a finite simple group. We subsequently prove this conjecture. This new toy theorem comments on the necessary properties of generators of finite simple groups. We show this explicitly for a class of sporadic groups for which the result holds. Our work further makes the case for a machine motivated study of algebraic structures in pure mathematics and highlights the possibility of generating new conjectures and theorems in mathematics with the aid of machine learning.

Mathematical conjecture generation using machine intelligence

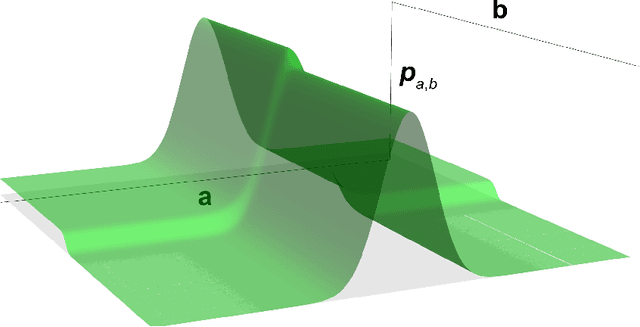
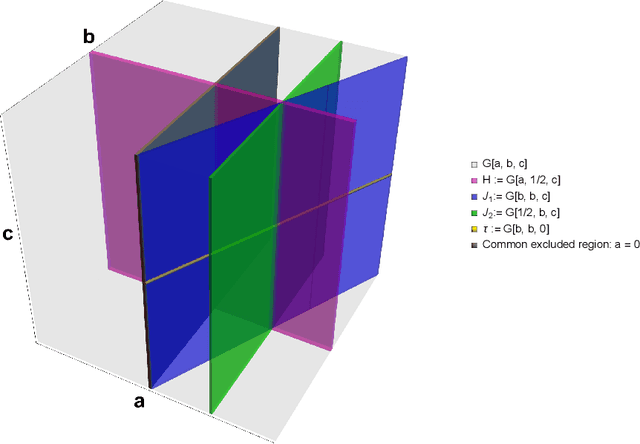
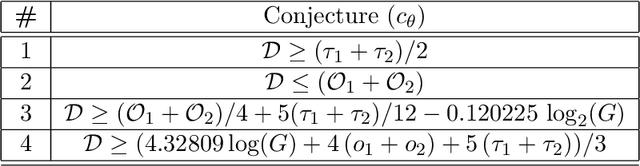
Conjectures have historically played an important role in the development of pure mathematics. We propose a systematic approach to finding abstract patterns in mathematical data, in order to generate conjectures about mathematical inequalities, using machine intelligence. We focus on strict inequalities of type f < g and associate them with a vector space. By geometerising this space, which we refer to as a conjecture space, we prove that this space is isomorphic to a Banach manifold. We develop a structural understanding of this conjecture space by studying linear automorphisms of this manifold and show that this space admits several free group actions. Based on these insights, we propose an algorithmic pipeline to generate novel conjectures using geometric gradient descent, where the metric is informed by the invariances of the conjecture space. As proof of concept, we give a toy algorithm to generate novel conjectures about the prime counting function and diameters of Cayley graphs of non-abelian simple groups. We also report private communications with colleagues in which some conjectures were proved, and highlight that some conjectures generated using this procedure are still unproven. Finally, we propose a pipeline of mathematical discovery in this space and highlight the importance of domain expertise in this pipeline.

A physics-informed search for metric solutions to Ricci flow, their embeddings, and visualisation

Neural networks with PDEs embedded in their loss functions (physics-informed neural networks) are employed as a function approximators to find solutions to the Ricci flow (a curvature based evolution) of Riemannian metrics. A general method is developed and applied to the real torus. The validity of the solution is verified by comparing the time evolution of scalar curvature with that found using a standard PDE solver, which decreases to a constant value of 0 on the whole manifold. We also consider certain solitonic solutions to the Ricci flow equation in two real dimensions. We create visualisations of the flow by utilising an embedding into $\mathbb{R}^3$. Snapshots of highly accurate numerical evolution of the toroidal metric over time are reported. We provide guidelines on applications of this methodology to the problem of determining Ricci flat Calabi--Yau metrics in the context of String theory, a long standing problem in complex geometry.

Machine Learned Calabi--Yau Metrics and Curvature

Finding Ricci-flat (Calabi--Yau) metrics is a long standing problem in geometry with deep implications for string theory and phenomenology. A new attack on this problem uses neural networks to engineer approximations to the Calabi--Yau metric within a given K\"ahler class. In this paper we investigate numerical Ricci-flat metrics over smooth and singular K3 surfaces and Calabi--Yau threefolds. Using these Ricci-flat metric approximations for the Cefal\'u and Dwork family of quartic twofolds and the Dwork family of quintic threefolds, we study characteristic forms on these geometries. Using persistent homology, we show that high curvature regions of the manifolds form clusters near the singular points, but also elsewhere. For our neural network approximations, we observe a Bogomolov--Yau type inequality $3c_2 \geq c_1^2$ and observe an identity when our geometries have isolated $A_1$ type singularities. We sketch a proof that $\chi(X~\smallsetminus~\mathrm{Sing}\,{X}) + 2~|\mathrm{Sing}\,{X}| = 24$ also holds for our numerical approximations.

Machine Learning for Optical Motion Capture-driven Musculoskeletal Modeling from Inertial Motion Capture Data

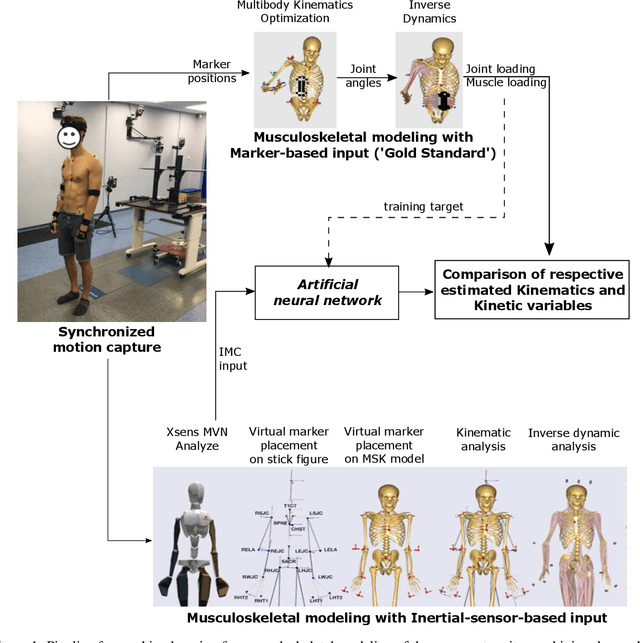
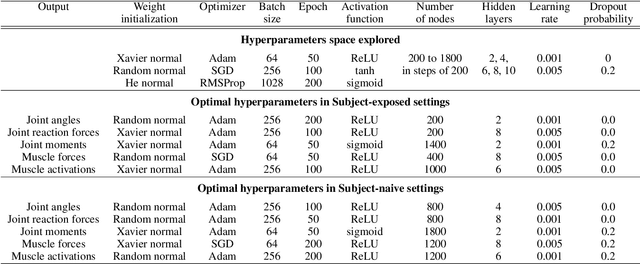
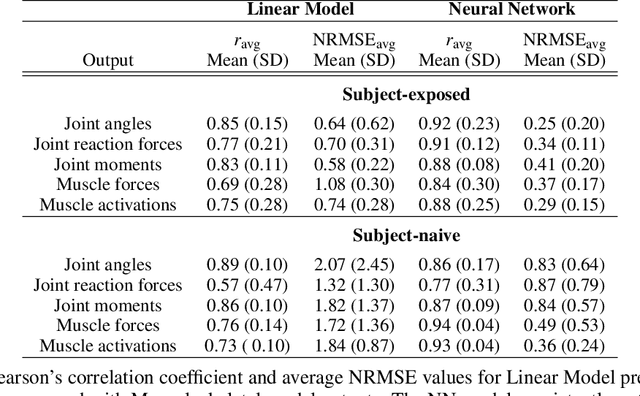
Marker-based Optical Motion Capture (OMC) systems and the associated musculoskeletal (MSK) modeling predictions have offered the ability to gain insights into in vivo joint and muscle loading non-invasively as well as aid clinical decision-making. However, an OMC system is lab-based, expensive, and requires a line of sight. A widely used alternative is the Inertial Motion Capture (IMC) system, which is portable, user-friendly, and relatively low cost, although it is not as accurate as an OMC system. Irrespective of the choice of motion capture technique, one needs to use an MSK model to obtain the kinematic and kinetic outputs, which is a computationally expensive tool increasingly well approximated by machine learning (ML) methods. Here, we present an ML approach to map IMC data to the human upper-extremity MSK outputs computed from OMC input data. Essentially, we attempt to predict high-quality MSK outputs from the relatively easier-to-obtain IMC data. We use OMC and IMC data simultaneously collected for the same subjects to train an ML (feed-forward multi-layer perceptron) model that predicts OMC-based MSK outputs from IMC measurements. We demonstrate that our ML predictions have a high degree of agreement with the desired OMC-based MSK estimates. Thus, this approach will be instrumental in getting the technology from 'lab to field' where OMC-based systems are infeasible.

Neural Network Approximations for Calabi-Yau Metrics

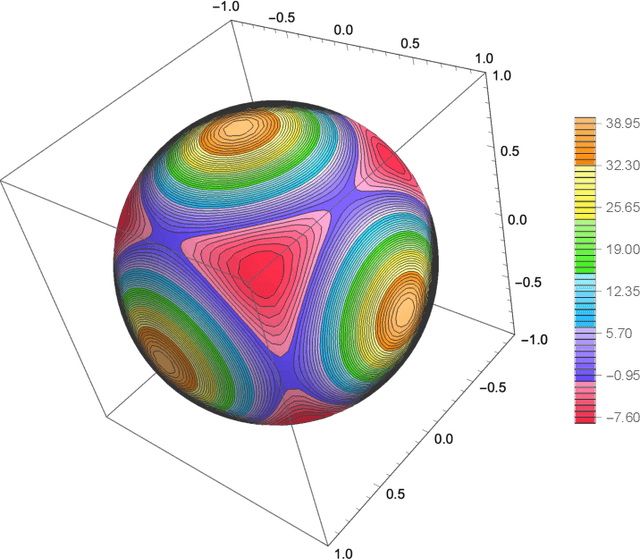
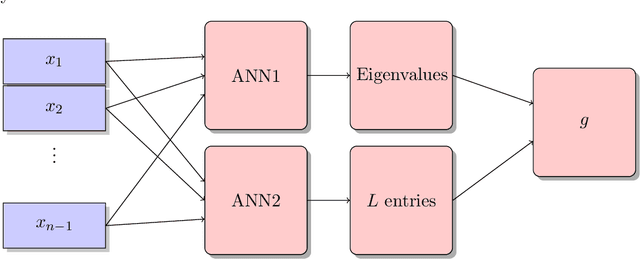
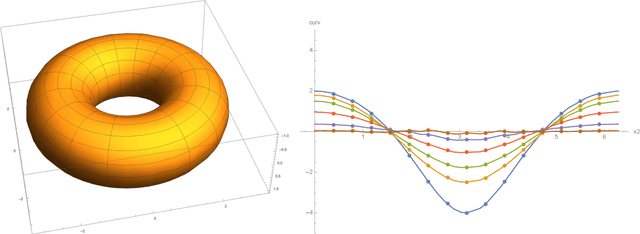
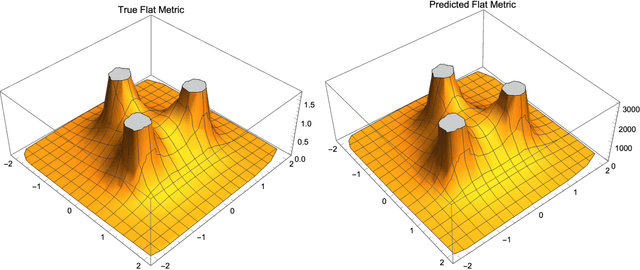
Ricci flat metrics for Calabi-Yau threefolds are not known analytically. In this work, we employ techniques from machine learning to deduce numerical flat metrics for the Fermat quintic, for the Dwork quintic, and for the Tian-Yau manifold. This investigation employs a single neural network architecture that is capable of approximating Ricci flat Kaehler metrics for several Calabi-Yau manifolds of dimensions two and three. We show that measures that assess the Ricci flatness of the geometry decrease after training by three orders of magnitude. This is corroborated on the validation set, where the improvement is more modest. Finally, we demonstrate that discrete symmetries of manifolds can be learned in the process of learning the metric.

Baryons from Mesons: A Machine Learning Perspective

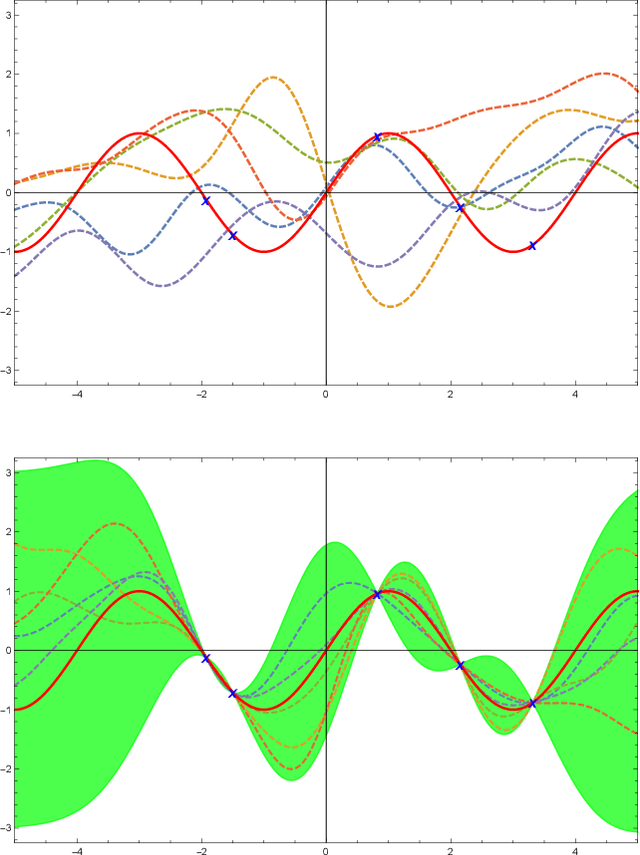
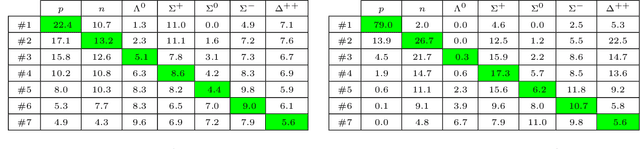
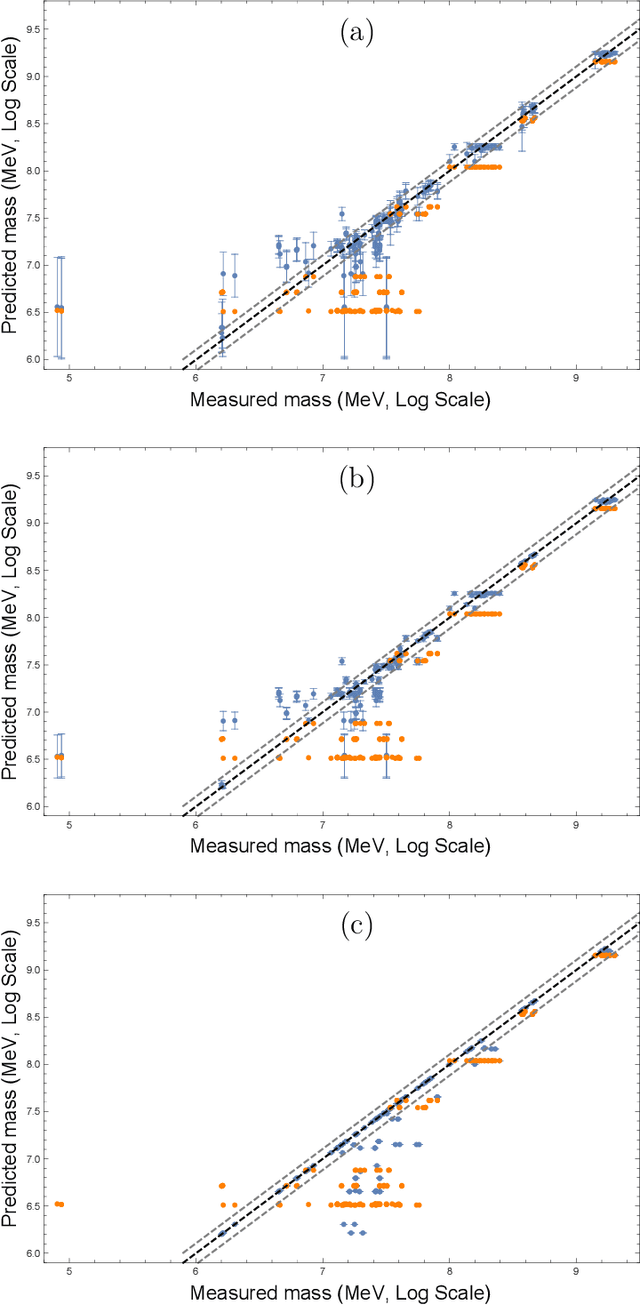
Quantum chromodynamics (QCD) is the theory of the strong interaction. The fundamental particles of QCD, quarks and gluons, carry colour charge and form colourless bound states at low energies. The hadronic bound states of primary interest to us are the mesons and the baryons. From knowledge of the meson spectrum, we use neural networks and Gaussian processes to predict the masses of baryons with 90.3% and 96.6% accuracy, respectively. These results compare favourably to the constituent quark model. We as well predict the masses of pentaquarks and other exotic hadrons.