Uniform $\mathcal{C}^k$ Approximation of $G$-Invariant and Antisymmetric Functions, Embedding Dimensions, and Polynomial Representations

For any subgroup $G$ of the symmetric group $\mathcal{S}_n$ on $n$ symbols, we present results for the uniform $\mathcal{C}^k$ approximation of $G$-invariant functions by $G$-invariant polynomials. For the case of totally symmetric functions ($G = \mathcal{S}_n$), we show that this gives rise to the sum-decomposition Deep Sets ansatz of Zaheer et al. (2018), where both the inner and outer functions can be chosen to be smooth, and moreover, the inner function can be chosen to be independent of the target function being approximated. In particular, we show that the embedding dimension required is independent of the regularity of the target function, the accuracy of the desired approximation, as well as $k$. Next, we show that a similar procedure allows us to obtain a uniform $\mathcal{C}^k$ approximation of antisymmetric functions as a sum of $K$ terms, where each term is a product of a smooth totally symmetric function and a smooth antisymmetric homogeneous polynomial of degree at most $\binom{n}{2}$. We also provide upper and lower bounds on $K$ and show that $K$ is independent of the regularity of the target function, the desired approximation accuracy, and $k$.

Mathematical conjecture generation using machine intelligence

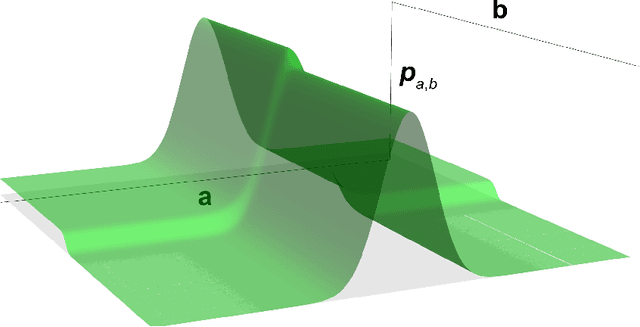
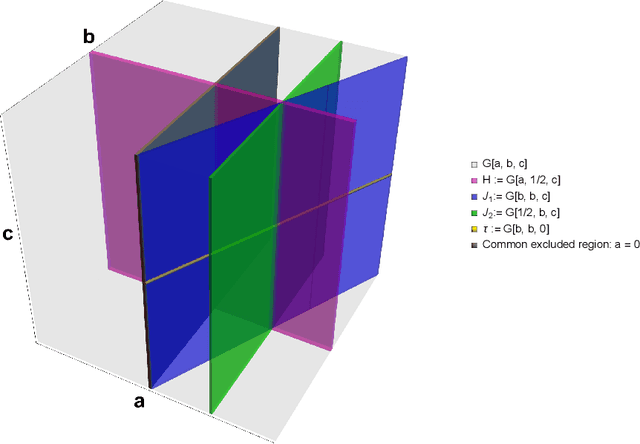
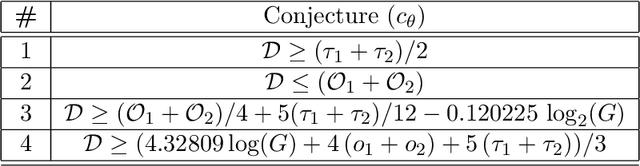
Conjectures have historically played an important role in the development of pure mathematics. We propose a systematic approach to finding abstract patterns in mathematical data, in order to generate conjectures about mathematical inequalities, using machine intelligence. We focus on strict inequalities of type f < g and associate them with a vector space. By geometerising this space, which we refer to as a conjecture space, we prove that this space is isomorphic to a Banach manifold. We develop a structural understanding of this conjecture space by studying linear automorphisms of this manifold and show that this space admits several free group actions. Based on these insights, we propose an algorithmic pipeline to generate novel conjectures using geometric gradient descent, where the metric is informed by the invariances of the conjecture space. As proof of concept, we give a toy algorithm to generate novel conjectures about the prime counting function and diameters of Cayley graphs of non-abelian simple groups. We also report private communications with colleagues in which some conjectures were proved, and highlight that some conjectures generated using this procedure are still unproven. Finally, we propose a pipeline of mathematical discovery in this space and highlight the importance of domain expertise in this pipeline.

An improvement to a result about graph isomorphism networks using the prime factorization theorem

The unique prime factorization theorem is used to show the existence of a function on a countable set $\mathcal{X}$ so that the sum aggregator function is injective on all multisets of $\mathcal{X}$ of finite size.