Machine learning automorphic forms for black holes

Modular, Jacobi, and mock-modular forms serve as generating functions for BPS black hole degeneracies. By training feed-forward neural networks on Fourier coefficients of automorphic forms derived from the Dedekind eta function, Eisenstein series, and Jacobi theta functions, we demonstrate that machine learning techniques can accurately predict modular weights from truncated expansions. Our results reveal strong performance for negative weight modular and quasi-modular forms, particularly those arising in exact black hole counting formulae, with lower accuracy for positive weights and more complicated combinations of Jacobi theta functions. This study establishes a proof of concept for using machine learning to identify how data is organized in terms of modular symmetries in gravitational systems and suggests a pathway toward automated detection and verification of symmetries in quantum gravity.

Colored Jones Polynomials and the Volume Conjecture

Using the vertex model approach for braid representations, we compute polynomials for spin-1 placed on hyperbolic knots up to 15 crossings. These polynomials are referred to as 3-colored Jones polynomials or adjoint Jones polynomials. Training a subset of the data using a fully connected feedforward neural network, we predict the volume of the knot complement of hyperbolic knots from the adjoint Jones polynomial or its evaluations with 99.34% accuracy. A function of the adjoint Jones polynomial evaluated at the phase $q=e^{ 8 \pi i / 15 }$ predicts the volume with nearly the same accuracy as the neural network. From an analysis of 2-colored and 3-colored Jones polynomials, we conjecture the best phase for $n$-colored Jones polynomials, and use this hypothesis to motivate an improved statement of the volume conjecture. This is tested for knots for which closed form expressions for the $n$-colored Jones polynomial are known, and we show improved convergence to the volume.

cymyc -- Calabi-Yau Metrics, Yukawas, and Curvature

We introduce \texttt{cymyc}, a high-performance Python library for numerical investigation of the geometry of a large class of string compactification manifolds and their associated moduli spaces. We develop a well-defined geometric ansatz to numerically model tensor fields of arbitrary degree on a large class of Calabi-Yau manifolds. \texttt{cymyc} includes a machine learning component which incorporates this ansatz to model tensor fields of interest on these spaces by finding an approximate solution to the system of partial differential equations they should satisfy.

Learning to be Simple

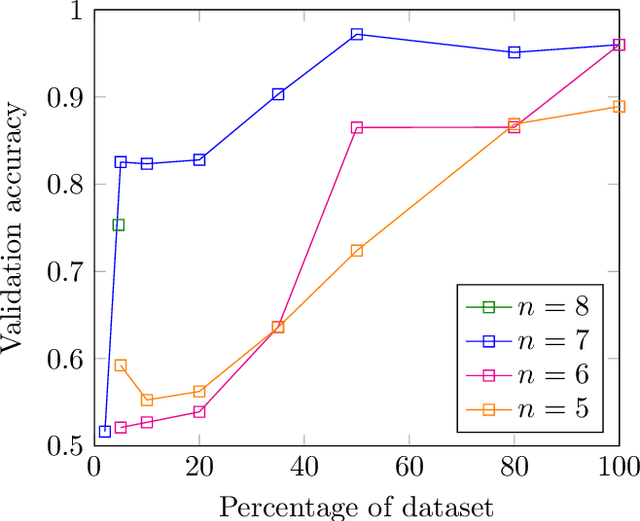
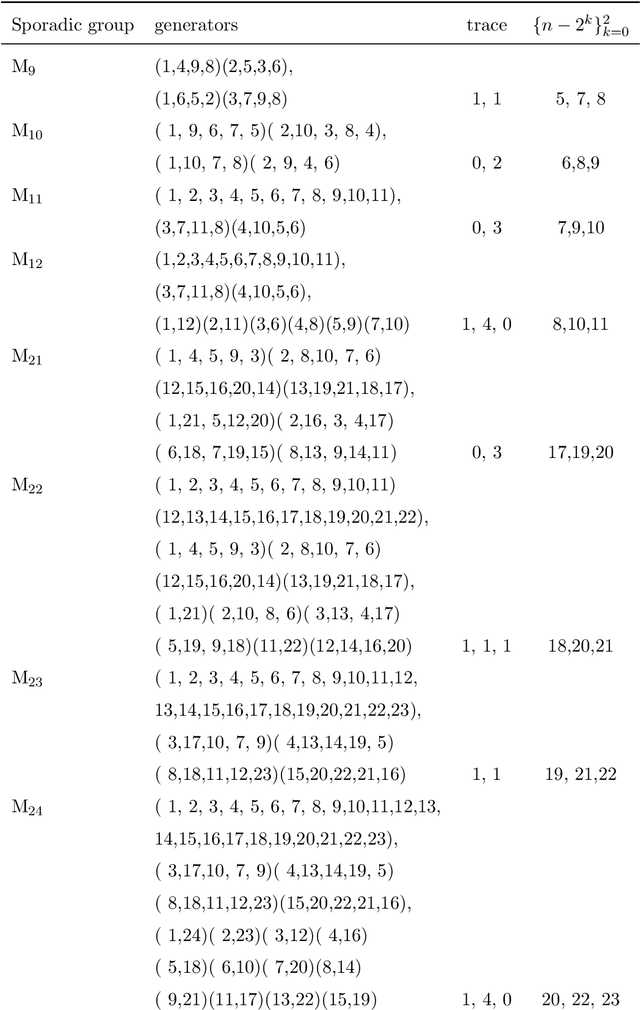
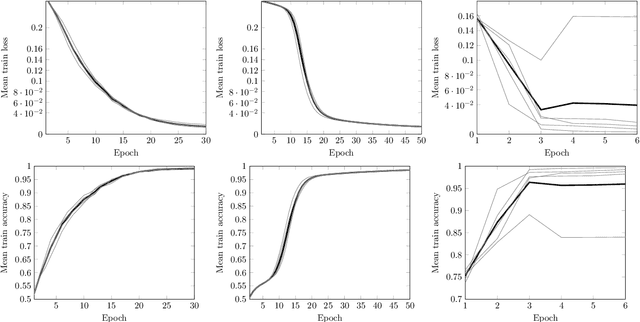
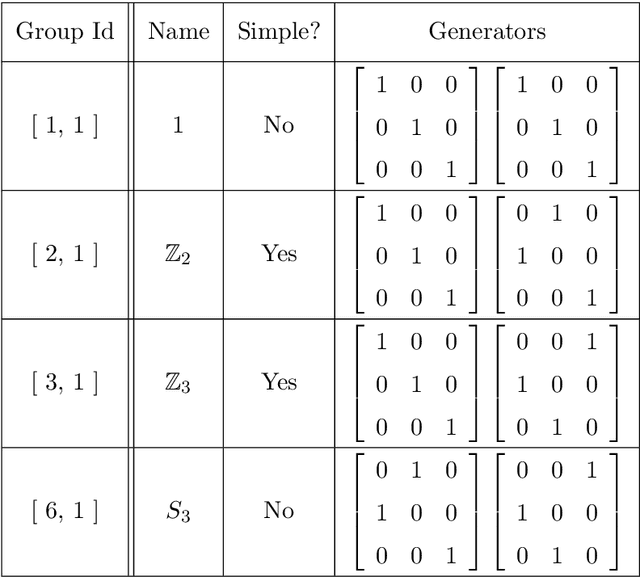
In this work we employ machine learning to understand structured mathematical data involving finite groups and derive a theorem about necessary properties of generators of finite simple groups. We create a database of all 2-generated subgroups of the symmetric group on n-objects and conduct a classification of finite simple groups among them using shallow feed-forward neural networks. We show that this neural network classifier can decipher the property of simplicity with varying accuracies depending on the features. Our neural network model leads to a natural conjecture concerning the generators of a finite simple group. We subsequently prove this conjecture. This new toy theorem comments on the necessary properties of generators of finite simple groups. We show this explicitly for a class of sporadic groups for which the result holds. Our work further makes the case for a machine motivated study of algebraic structures in pure mathematics and highlights the possibility of generating new conjectures and theorems in mathematics with the aid of machine learning.

Machine Learned Calabi--Yau Metrics and Curvature

Finding Ricci-flat (Calabi--Yau) metrics is a long standing problem in geometry with deep implications for string theory and phenomenology. A new attack on this problem uses neural networks to engineer approximations to the Calabi--Yau metric within a given K\"ahler class. In this paper we investigate numerical Ricci-flat metrics over smooth and singular K3 surfaces and Calabi--Yau threefolds. Using these Ricci-flat metric approximations for the Cefal\'u and Dwork family of quartic twofolds and the Dwork family of quintic threefolds, we study characteristic forms on these geometries. Using persistent homology, we show that high curvature regions of the manifolds form clusters near the singular points, but also elsewhere. For our neural network approximations, we observe a Bogomolov--Yau type inequality $3c_2 \geq c_1^2$ and observe an identity when our geometries have isolated $A_1$ type singularities. We sketch a proof that $\chi(X~\smallsetminus~\mathrm{Sing}\,{X}) + 2~|\mathrm{Sing}\,{X}| = 24$ also holds for our numerical approximations.

Towards Quantum Advantage on Noisy Quantum Computers

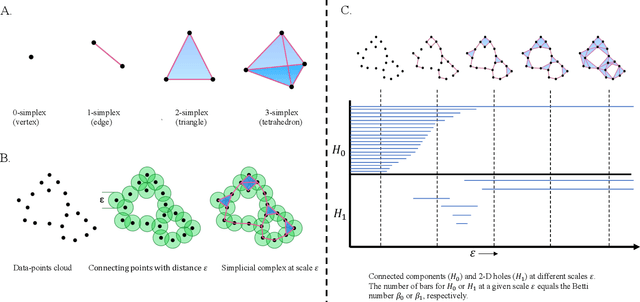
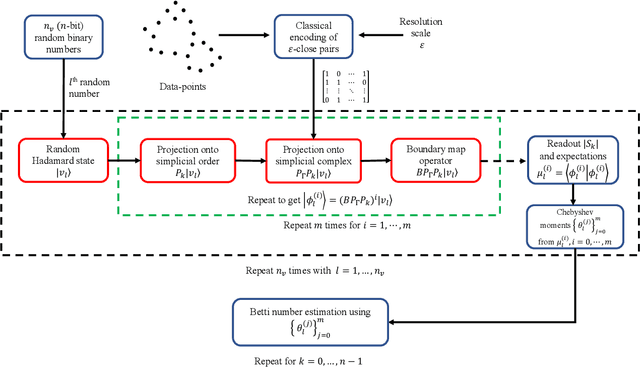
Topological data analysis (TDA) is a powerful technique for extracting complex and valuable shape-related summaries of high-dimensional data. However, the computational demands of classical TDA algorithms are exorbitant, and quickly become impractical for high-order characteristics. Quantum computing promises exponential speedup for certain problems. Yet, many existing quantum algorithms with notable asymptotic speedups require a degree of fault tolerance that is currently unavailable. In this paper, we present NISQ-TDA, the first fully implemented end-to-end quantum machine learning algorithm needing only a linear circuit-depth, that is applicable to non-handcrafted high-dimensional classical data, with potential speedup under stringent conditions. The algorithm neither suffers from the data-loading problem nor does it need to store the input data on the quantum computer explicitly. Our approach includes three key innovations: (a) an efficient realization of the full boundary operator as a sum of Pauli operators; (b) a quantum rejection sampling and projection approach to restrict a uniform superposition to the simplices of the desired order in the complex; and (c) a stochastic rank estimation method to estimate the topological features in the form of approximate Betti numbers. We present theoretical results that establish additive error guarantees for NISQ-TDA, and the circuit and computational time and depth complexities for exponentially scaled output estimates, up to the error tolerance. The algorithm was successfully executed on quantum computing devices, as well as on noisy quantum simulators, applied to small datasets. Preliminary empirical results suggest that the algorithm is robust to noise.

Identifying equivalent Calabi--Yau topologies: A discrete challenge from math and physics for machine learning

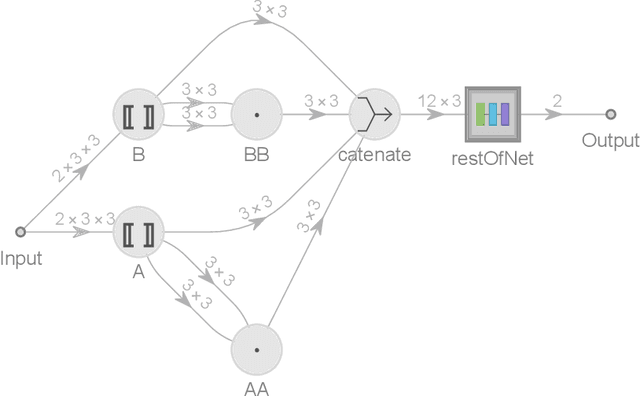
We review briefly the characteristic topological data of Calabi--Yau threefolds and focus on the question of when two threefolds are equivalent through related topological data. This provides an interesting test case for machine learning methodology in discrete mathematics problems motivated by physics.

Machine Learning Kreuzer--Skarke Calabi--Yau Threefolds

Using a fully connected feedforward neural network we study topological invariants of a class of Calabi--Yau manifolds constructed as hypersurfaces in toric varieties associated with reflexive polytopes from the Kreuzer--Skarke database. In particular, we find the existence of a simple expression for the Euler number that can be learned in terms of limited data extracted from the polytope and its dual.

Learning knot invariants across dimensions

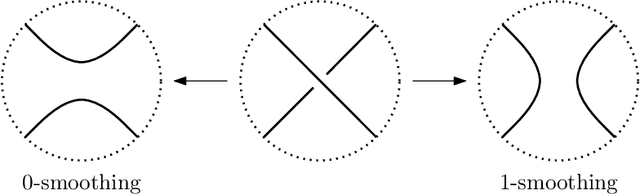
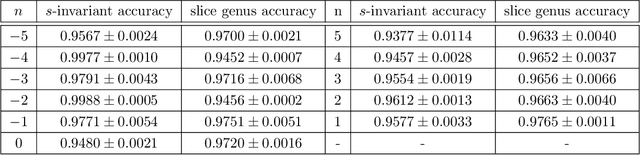
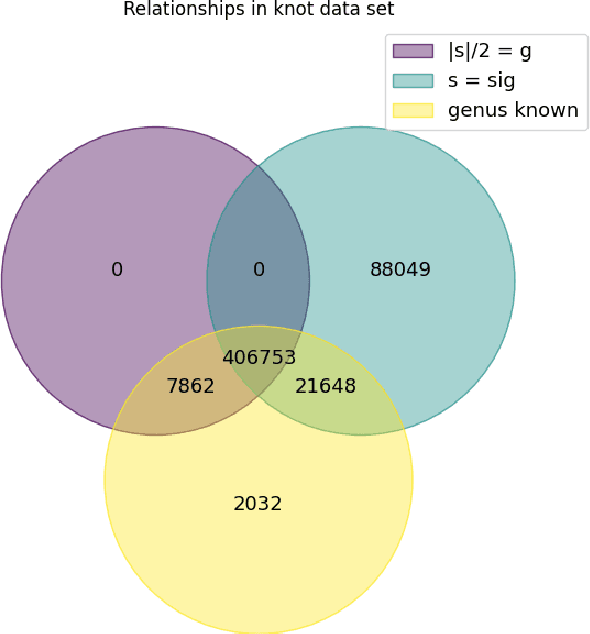
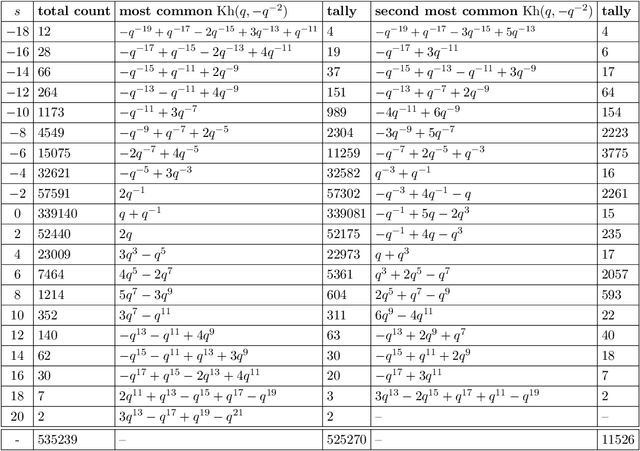
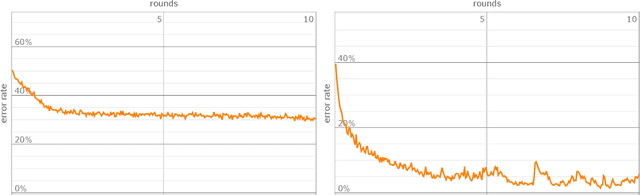
We use deep neural networks to machine learn correlations between knot invariants in various dimensions. The three-dimensional invariant of interest is the Jones polynomial $J(q)$, and the four-dimensional invariants are the Khovanov polynomial $\text{Kh}(q,t)$, smooth slice genus $g$, and Rasmussen's $s$-invariant. We find that a two-layer feed-forward neural network can predict $s$ from $\text{Kh}(q,-q^{-4})$ with greater than $99\%$ accuracy. A theoretical explanation for this performance exists in knot theory via the now disproven knight move conjecture, which is obeyed by all knots in our dataset. More surprisingly, we find similar performance for the prediction of $s$ from $\text{Kh}(q,-q^{-2})$, which suggests a novel relationship between the Khovanov and Lee homology theories of a knot. The network predicts $g$ from $\text{Kh}(q,t)$ with similarly high accuracy, and we discuss the extent to which the machine is learning $s$ as opposed to $g$, since there is a general inequality $|s| \leq 2g$. The Jones polynomial, as a three-dimensional invariant, is not obviously related to $s$ or $g$, but the network achieves greater than $95\%$ accuracy in predicting either from $J(q)$. Moreover, similar accuracy can be achieved by evaluating $J(q)$ at roots of unity. This suggests a relationship with $SU(2)$ Chern--Simons theory, and we review the gauge theory construction of Khovanov homology which may be relevant for explaining the network's performance.

Neural Network Approximations for Calabi-Yau Metrics

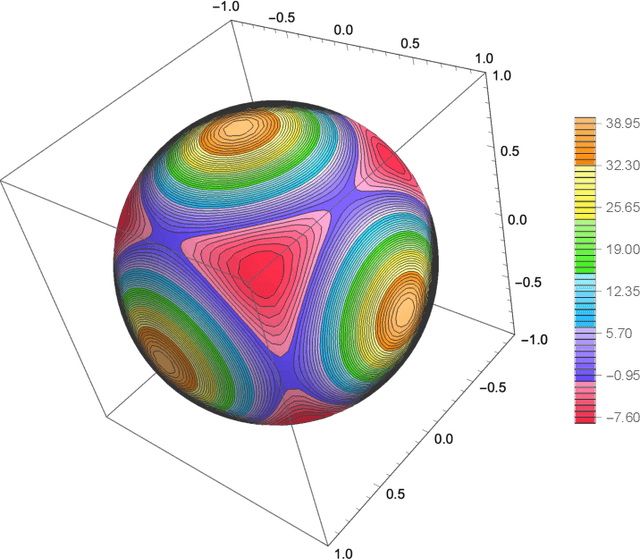
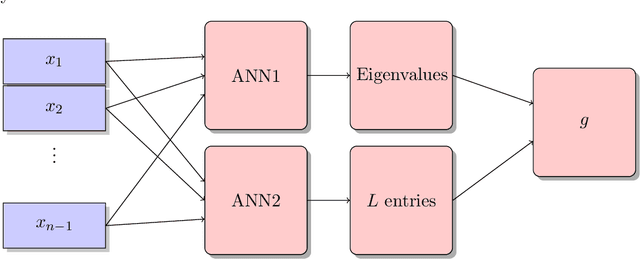
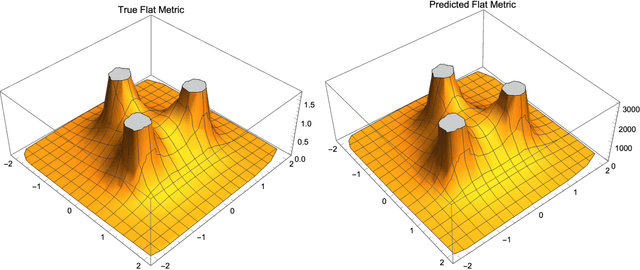
Ricci flat metrics for Calabi-Yau threefolds are not known analytically. In this work, we employ techniques from machine learning to deduce numerical flat metrics for the Fermat quintic, for the Dwork quintic, and for the Tian-Yau manifold. This investigation employs a single neural network architecture that is capable of approximating Ricci flat Kaehler metrics for several Calabi-Yau manifolds of dimensions two and three. We show that measures that assess the Ricci flatness of the geometry decrease after training by three orders of magnitude. This is corroborated on the validation set, where the improvement is more modest. Finally, we demonstrate that discrete symmetries of manifolds can be learned in the process of learning the metric.