Low Complexity Regularized Phase Retrieval

In this paper, we study the phase retrieval problem in the situation where the vector to be recovered has an a priori structure that can encoded into a regularization term. This regularizer is intended to promote solutions conforming to some notion of simplicity or low complexity. We investigate both noiseless recovery and stability to noise and provide a very general and unified analysis framework that goes far beyond the sparse phase retrieval mostly considered in the literature. In the noiseless case we provide sufficient conditions under which exact recovery, up to global sign change, is possible. For Gaussian measurement maps, we also provide a sample complexity bound for exact recovery. This bound depends on the Gaussian width of the descent cone at the soughtafter vector which is a geometric measure of the complexity of the latter. In the noisy case, we consider both the constrained (Mozorov) and penalized (Tikhonov) formulations. We provide sufficient conditions for stable recovery and prove linear convergence for sufficiently small noise. For Gaussian measurements, we again give a sample complexity bound for linear convergence to hold with high probability. This bound scales linearly in the intrinsic dimension of the sought-after vector but only logarithmically in the ambient dimension.

Stable Phase Retrieval with Mirror Descent

In this paper, we aim to reconstruct an n-dimensional real vector from m phaseless measurements corrupted by an additive noise. We extend the noiseless framework developed in [15], based on mirror descent (or Bregman gradient descent), to deal with noisy measurements and prove that the procedure is stable to (small enough) additive noise. In the deterministic case, we show that mirror descent converges to a critical point of the phase retrieval problem, and if the algorithm is well initialized and the noise is small enough, the critical point is near the true vector up to a global sign change. When the measurements are i.i.d Gaussian and the signal-to-noise ratio is large enough, we provide global convergence guarantees that ensure that with high probability, mirror descent converges to a global minimizer near the true vector (up to a global sign change), as soon as the number of measurements m is large enough. The sample complexity bound can be improved if a spectral method is used to provide a good initial guess. We complement our theoretical study with several numerical results showing that mirror descent is both a computationally and statistically efficient scheme to solve the phase retrieval problem.

Learning-to-Optimize with PAC-Bayesian Guarantees: Theoretical Considerations and Practical Implementation

We use the PAC-Bayesian theory for the setting of learning-to-optimize. To the best of our knowledge, we present the first framework to learn optimization algorithms with provable generalization guarantees (PAC-Bayesian bounds) and explicit trade-off between convergence guarantees and convergence speed, which contrasts with the typical worst-case analysis. Our learned optimization algorithms provably outperform related ones derived from a (deterministic) worst-case analysis. The results rely on PAC-Bayesian bounds for general, possibly unbounded loss-functions based on exponential families. Then, we reformulate the learning procedure into a one-dimensional minimization problem and study the possibility to find a global minimum. Furthermore, we provide a concrete algorithmic realization of the framework and new methodologies for learning-to-optimize, and we conduct four practically relevant experiments to support our theory. With this, we showcase that the provided learning framework yields optimization algorithms that provably outperform the state-of-the-art by orders of magnitude.

Recovery Guarantees of Unsupervised Neural Networks for Inverse Problems trained with Gradient Descent

Advanced machine learning methods, and more prominently neural networks, have become standard to solve inverse problems over the last years. However, the theoretical recovery guarantees of such methods are still scarce and difficult to achieve. Only recently did unsupervised methods such as Deep Image Prior (DIP) get equipped with convergence and recovery guarantees for generic loss functions when trained through gradient flow with an appropriate initialization. In this paper, we extend these results by proving that these guarantees hold true when using gradient descent with an appropriately chosen step-size/learning rate. We also show that the discretization only affects the overparametrization bound for a two-layer DIP network by a constant and thus that the different guarantees found for the gradient flow will hold for gradient descent.

Convergence and Recovery Guarantees of Unsupervised Neural Networks for Inverse Problems

Neural networks have become a prominent approach to solve inverse problems in recent years. While a plethora of such methods was developed to solve inverse problems empirically, we are still lacking clear theoretical guarantees for these methods. On the other hand, many works proved convergence to optimal solutions of neural networks in a more general setting using overparametrization as a way to control the Neural Tangent Kernel. In this work we investigate how to bridge these two worlds and we provide deterministic convergence and recovery guarantees for the class of unsupervised feedforward multilayer neural networks trained to solve inverse problems. We also derive overparametrization bounds under which a two-layers Deep Inverse Prior network with smooth activation function will benefit from our guarantees.

Convergence Guarantees of Overparametrized Wide Deep Inverse Prior

Neural networks have become a prominent approach to solve inverse problems in recent years. Amongst the different existing methods, the Deep Image/Inverse Priors (DIPs) technique is an unsupervised approach that optimizes a highly overparametrized neural network to transform a random input into an object whose image under the forward model matches the observation. However, the level of overparametrization necessary for such methods remains an open problem. In this work, we aim to investigate this question for a two-layers neural network with a smooth activation function. We provide overparametrization bounds under which such network trained via continuous-time gradient descent will converge exponentially fast with high probability which allows to derive recovery prediction bounds. This work is thus a first step towards a theoretical understanding of overparametrized DIP networks, and more broadly it participates to the theoretical understanding of neural networks in inverse problem settings.

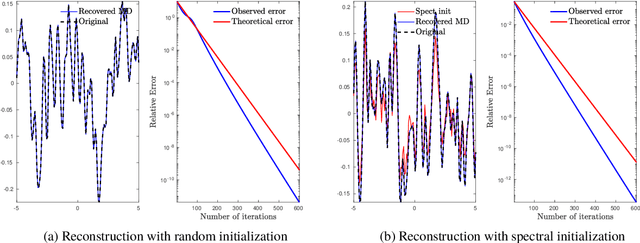
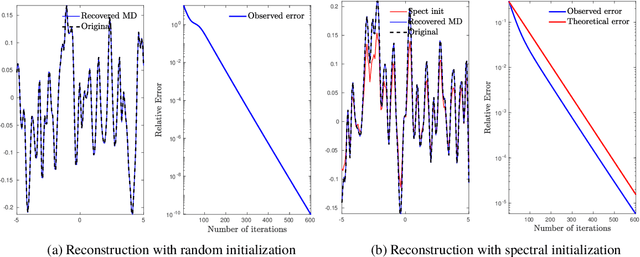
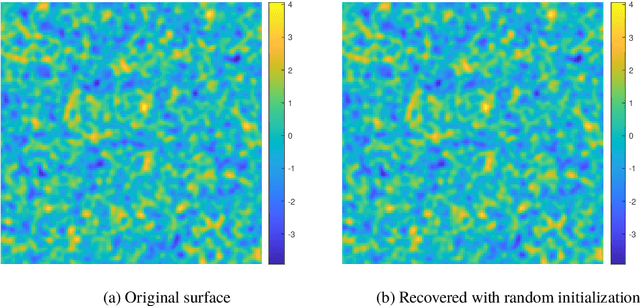
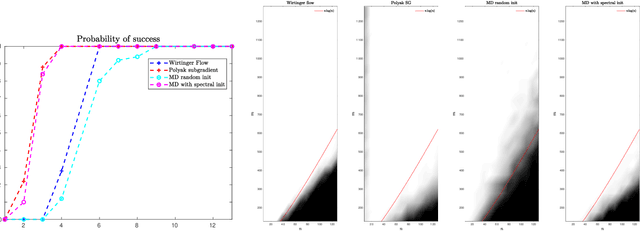
Provable Phase Retrieval with Mirror Descent

In this paper, we consider the problem of phase retrieval, which consists of recovering an $n$-dimensional real vector from the magnitude of its $m$ linear measurements. We propose a mirror descent (or Bregman gradient descent) algorithm based on a wisely chosen Bregman divergence, hence allowing to remove the classical global Lipschitz continuity requirement on the gradient of the non-convex phase retrieval objective to be minimized. We apply the mirror descent for two random measurements: the \iid standard Gaussian and those obtained by multiple structured illuminations through Coded Diffraction Patterns (CDP). For the Gaussian case, we show that when the number of measurements $m$ is large enough, then with high probability, for almost all initializers, the algorithm recovers the original vector up to a global sign change. For both measurements, the mirror descent exhibits a local linear convergence behaviour with a dimension-independent convergence rate. Our theoretical results are finally illustrated with various numerical experiments, including an application to the reconstruction of images in precision optics.

A Stochastic Bregman Primal-Dual Splitting Algorithm for Composite Optimization

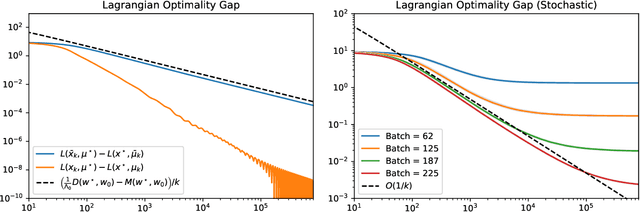
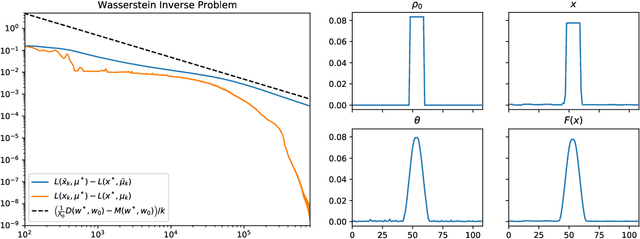
We study a stochastic first order primal-dual method for solving convex-concave saddle point problems over real reflexive Banach spaces using Bregman divergences and relative smoothness assumptions, in which we allow for stochastic error in the computation of gradient terms within the algorithm. We show ergodic convergence in expectation of the Lagrangian optimality gap with a rate of O(1/k) and that every almost sure weak cluster point of the ergodic sequence is a saddle point in expectation under mild assumptions. Under slightly stricter assumptions, we show almost sure weak convergence of the pointwise iterates to a saddle point. Under a relative strong convexity assumption on the objective functions and a total convexity assumption on the entropies of the Bregman divergences, we establish almost sure strong convergence of the pointwise iterates to a saddle point. Our framework is general and does not need strong convexity of the entropies inducing the Bregman divergences in the algorithm. Numerical applications are considered including entropically regularized Wasserstein barycenter problems and regularized inverse problems on the simplex.

Global Convergence of Model Function Based Bregman Proximal Minimization Algorithms

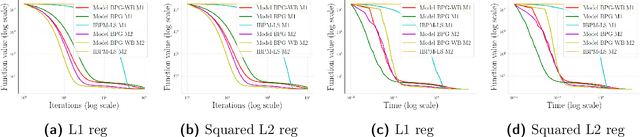
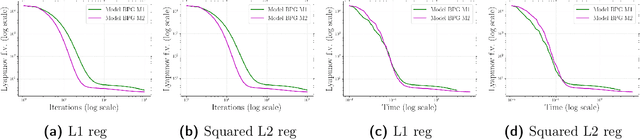
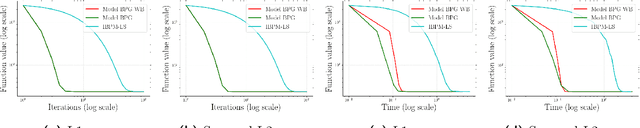
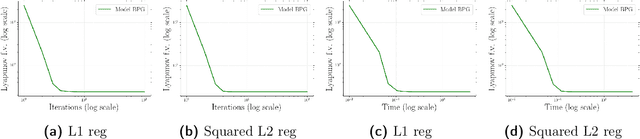
Lipschitz continuity of the gradient mapping of a continuously differentiable function plays a crucial role in designing various optimization algorithms. However, many functions arising in practical applications such as low rank matrix factorization or deep neural network problems do not have a Lipschitz continuous gradient. This led to the development of a generalized notion known as the $L$-smad property, which is based on generalized proximity measures called Bregman distances. However, the $L$-smad property cannot handle nonsmooth functions, for example, simple nonsmooth functions like $\abs{x^4-1}$ and also many practical composite problems are out of scope. We fix this issue by proposing the MAP property, which generalizes the $L$-smad property and is also valid for a large class of nonconvex nonsmooth composite problems. Based on the proposed MAP property, we propose a globally convergent algorithm called Model BPG, that unifies several existing algorithms. The convergence analysis is based on a new Lyapunov function. We also numerically illustrate the superior performance of Model BPG on standard phase retrieval problems, robust phase retrieval problems, and Poisson linear inverse problems, when compared to a state of the art optimization method that is valid for generic nonconvex nonsmooth optimization problems.

Inexact and Stochastic Generalized Conditional Gradient with Augmented Lagrangian and Proximal Step

In this paper we propose and analyze inexact and stochastic versions of the CGALP algorithm developed in the authors' previous paper, which we denote ICGALP, that allows for errors in the computation of several important quantities. In particular this allows one to compute some gradients, proximal terms, and/or linear minimization oracles in an inexact fashion that facilitates the practical application of the algorithm to computationally intensive settings, e.g. in high (or possibly infinite) dimensional Hilbert spaces commonly found in machine learning problems. The algorithm is able to solve composite minimization problems involving the sum of three convex proper lower-semicontinuous functions subject to an affine constraint of the form $Ax=b$ for some bounded linear operator $A$. Only one of the functions in the objective is assumed to be differentiable, the other two are assumed to have an accessible prox operator and a linear minimization oracle. As main results, we show convergence of the Lagrangian to an optimum and asymptotic feasibility of the affine constraint as well as weak convergence of the dual variable to a solution of the dual problem, all in an almost sure sense. Almost sure convergence rates, both pointwise and ergodic, are given for the Lagrangian values and the feasibility gap. Numerical experiments verifying the predicted rates of convergence are shown as well.