Stochastic batch size for adaptive regularization in deep network optimization

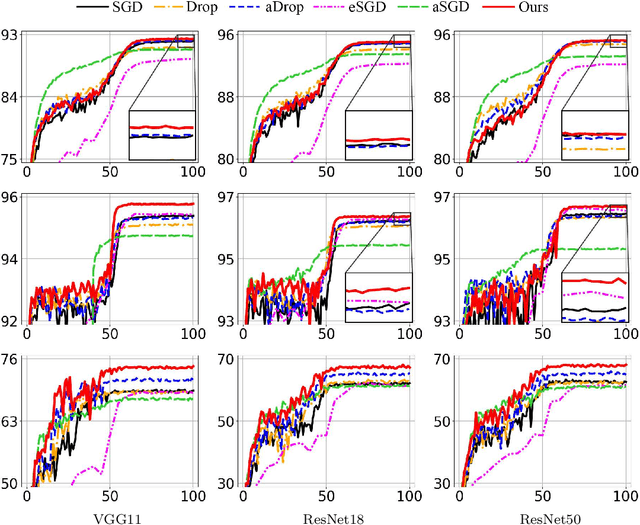
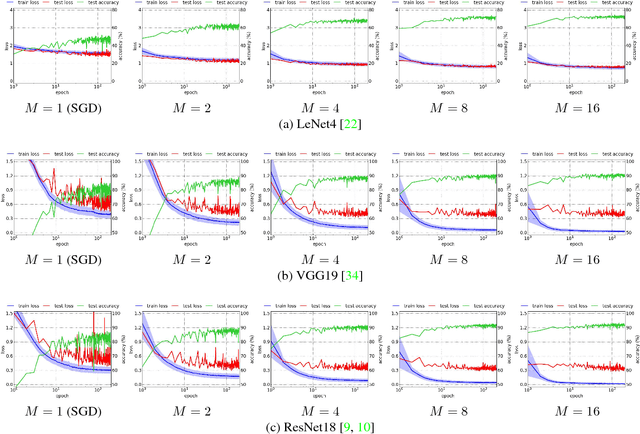
We propose a first-order stochastic optimization algorithm incorporating adaptive regularization applicable to machine learning problems in deep learning framework. The adaptive regularization is imposed by stochastic process in determining batch size for each model parameter at each optimization iteration. The stochastic batch size is determined by the update probability of each parameter following a distribution of gradient norms in consideration of their local and global properties in the neural network architecture where the range of gradient norms may vary within and across layers. We empirically demonstrate the effectiveness of our algorithm using an image classification task based on conventional network models applied to commonly used benchmark datasets. The quantitative evaluation indicates that our algorithm outperforms the state-of-the-art optimization algorithms in generalization while providing less sensitivity to the selection of batch size which often plays a critical role in optimization, thus achieving more robustness to the selection of regularity.

Adaptive Regularization via Residual Smoothing in Deep Learning Optimization

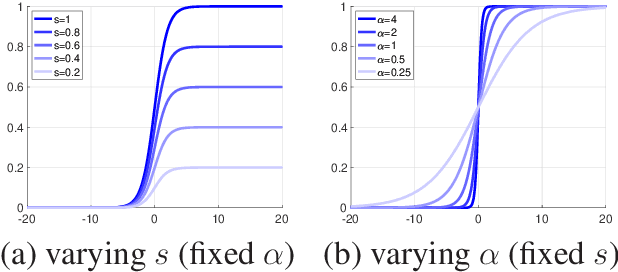
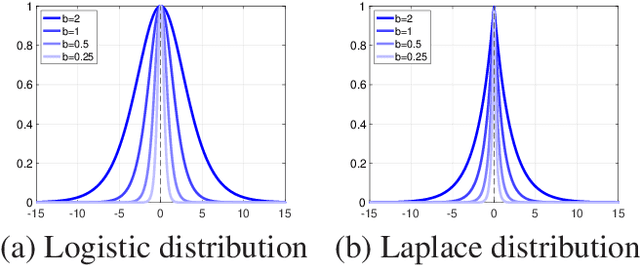
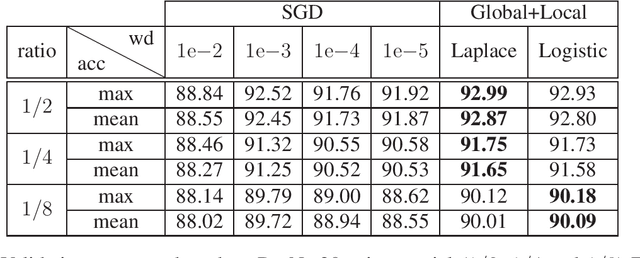
We present an adaptive regularization algorithm that can be effectively applied to the optimization problem in deep learning framework. Our regularization algorithm aims to take into account the fitness of data to the current state of model in the determination of regularity to achieve better generalization. The degree of regularization at each element in the target space of the neural network architecture is determined based on the residual at each optimization iteration in an adaptive way. Our adaptive regularization algorithm is designed to apply a diffusion process driven by the heat equation with spatially varying diffusivity depending on the probability density function following a certain distribution of residual. Our data-driven regularity is imposed by adaptively smoothing a simplified objective function in which the explicit regularization term is omitted in an alternating manner between the evaluation of residual and the determination of the degree of its regularity. The effectiveness of our algorithm is empirically demonstrated by the numerical experiments in the application of image classification problems, indicating that our algorithm outperforms other commonly used optimization algorithms in terms of generalization using popular deep learning models and benchmark datasets.

Adaptive Weight Decay for Deep Neural Networks

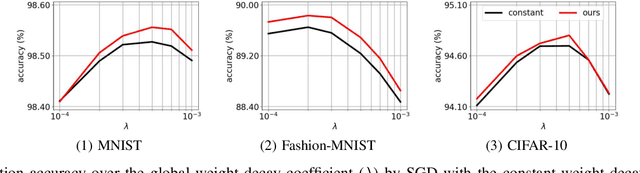
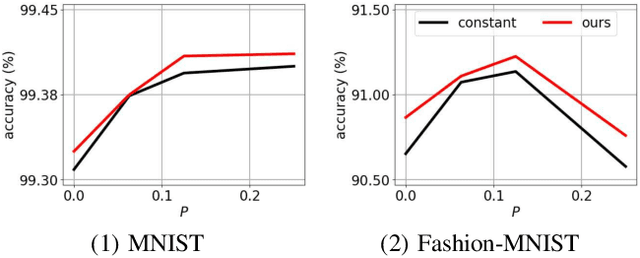
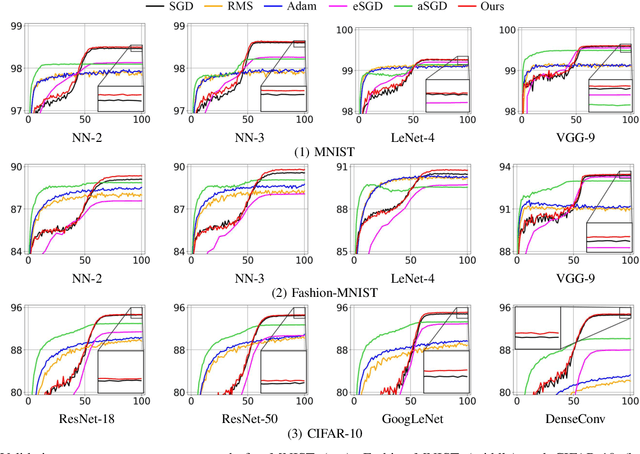
Regularization in the optimization of deep neural networks is often critical to avoid undesirable over-fitting leading to better generalization of model. One of the most popular regularization algorithms is to impose L-2 penalty on the model parameters resulting in the decay of parameters, called weight-decay, and the decay rate is generally constant to all the model parameters in the course of optimization. In contrast to the previous approach based on the constant rate of weight-decay, we propose to consider the residual that measures dissimilarity between the current state of model and observations in the determination of the weight-decay for each parameter in an adaptive way, called adaptive weight-decay (AdaDecay) where the gradient norms are normalized within each layer and the degree of regularization for each parameter is determined in proportional to the magnitude of its gradient using the sigmoid function. We empirically demonstrate the effectiveness of AdaDecay in comparison to the state-of-the-art optimization algorithms using popular benchmark datasets: MNIST, Fashion-MNIST, and CIFAR-10 with conventional neural network models ranging from shallow to deep. The quantitative evaluation of our proposed algorithm indicates that AdaDecay improves generalization leading to better accuracy across all the datasets and models.

Bilateral Cyclic Constraint and Adaptive Regularization for Unsupervised Monocular Depth Prediction

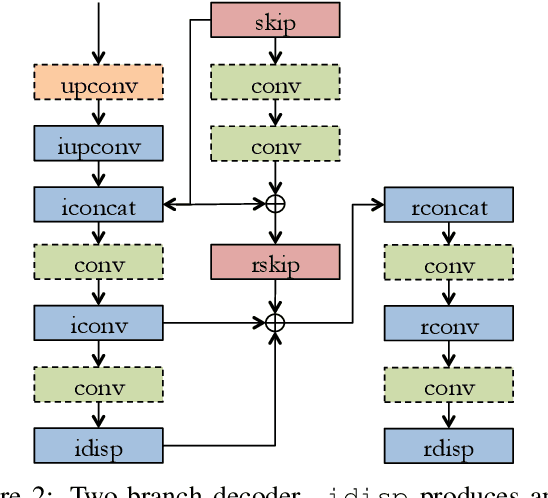
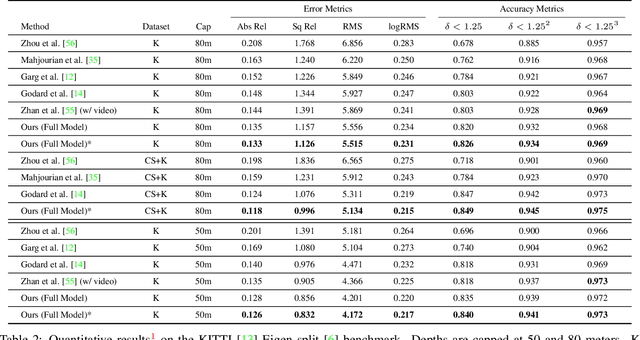
Supervised learning methods to infer (hypothesize) depth of a scene from a single image require costly per-pixel ground-truth. We follow a geometric approach that exploits abundant stereo imagery to learn a model to hypothesize scene structure without direct supervision. Although we train a network with stereo pairs, we only require a single image at test time to hypothesize disparity or depth. We propose a novel objective function that exploits the bilateral cyclic relationship between the left and right disparities and we introduce an adaptive regularization scheme that allows the network to handle both the co-visible and occluded regions in a stereo pair. This process ultimately produces a model to generate hypotheses for the 3-dimensional structure of the scene as viewed in a single image. When used to generate a single (most probable) estimate of depth, our method outperforms state-of-the-art unsupervised monocular depth prediction methods on the KITTI benchmarks. We show that our method generalizes well by applying our models trained on KITTI to the Make3d dataset.

Block-Cyclic Stochastic Coordinate Descent for Deep Neural Networks

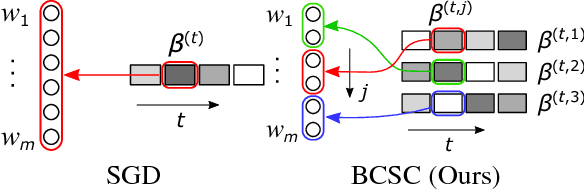
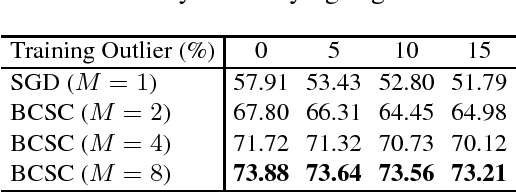
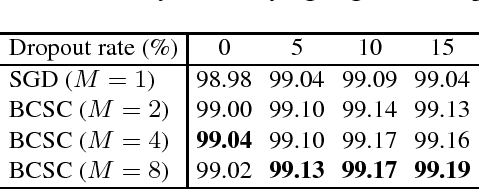
We present a stochastic first-order optimization algorithm, named BCSC, that adds a cyclic constraint to stochastic block-coordinate descent. It uses different subsets of the data to update different subsets of the parameters, thus limiting the detrimental effect of outliers in the training set. Empirical tests in benchmark datasets show that our algorithm outperforms state-of-the-art optimization methods in both accuracy as well as convergence speed. The improvements are consistent across different architectures, and can be combined with other training techniques and regularization methods.

Adaptive Regularization of Some Inverse Problems in Image Analysis

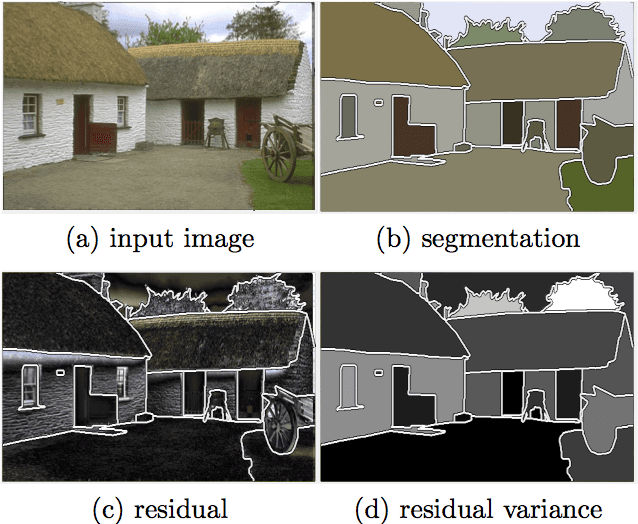
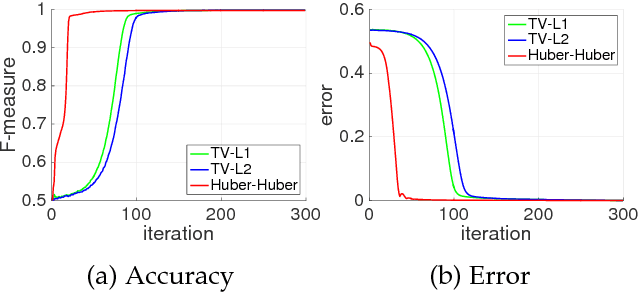
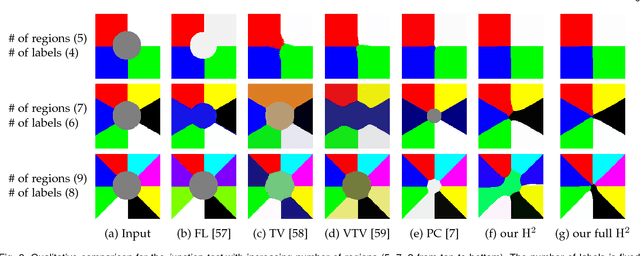
We present an adaptive regularization scheme for optimizing composite energy functionals arising in image analysis problems. The scheme automatically trades off data fidelity and regularization depending on the current data fit during the iterative optimization, so that regularization is strongest initially, and wanes as data fidelity improves, with the weight of the regularizer being minimized at convergence. We also introduce the use of a Huber loss function in both data fidelity and regularization terms, and present an efficient convex optimization algorithm based on the alternating direction method of multipliers (ADMM) using the equivalent relation between the Huber function and the proximal operator of the one-norm. We illustrate and validate our adaptive Huber-Huber model on synthetic and real images in segmentation, motion estimation, and denoising problems.

Adaptive Regularization in Convex Composite Optimization for Variational Imaging Problems

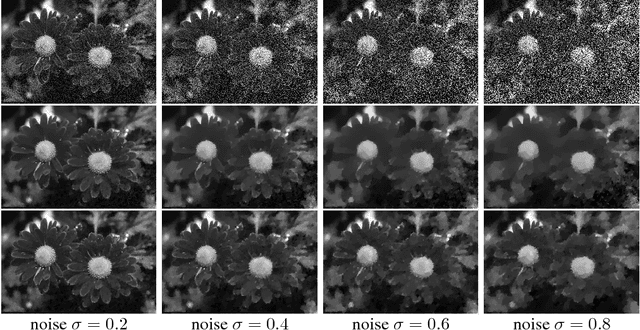
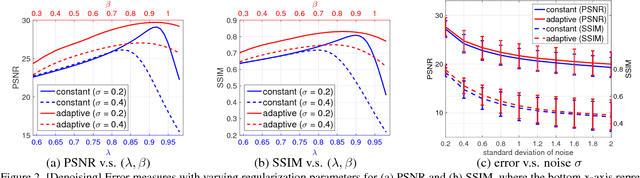
We propose an adaptive regularization scheme in a variational framework where a convex composite energy functional is optimized. We consider a number of imaging problems including denoising, segmentation and motion estimation, which are considered as optimal solutions of the energy functionals that mainly consist of data fidelity, regularization and a control parameter for their trade-off. We presents an algorithm to determine the relative weight between data fidelity and regularization based on the residual that measures how well the observation fits the model. Our adaptive regularization scheme is designed to locally control the regularization at each pixel based on the assumption that the diversity of the residual of a given imaging model spatially varies. The energy optimization is presented in the alternating direction method of multipliers (ADMM) framework where the adaptive regularization is iteratively applied along with mathematical analysis of the proposed algorithm. We demonstrate the robustness and effectiveness of our adaptive regularization through experimental results presenting that the qualitative and quantitative evaluation results of each imaging task are superior to the results with a constant regularization scheme. The desired properties, robustness and effectiveness, of the regularization parameter selection in a variational framework for imaging problems are achieved by merely replacing the static regularization parameter with our adaptive one.

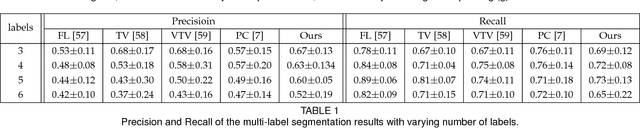
Multi-Label Segmentation via Residual-Driven Adaptive Regularization

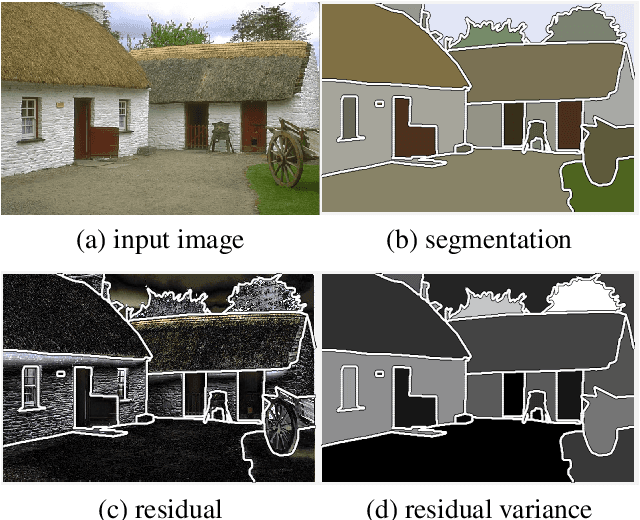
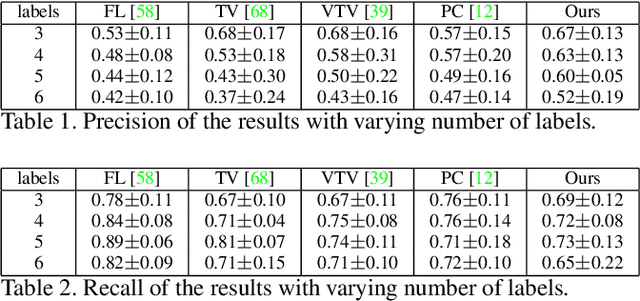
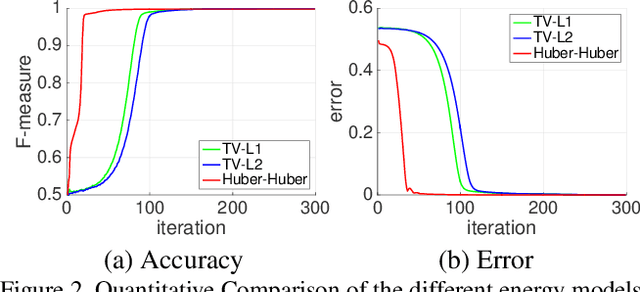
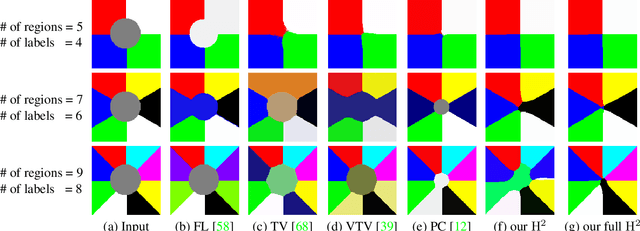
We present a variational multi-label segmentation algorithm based on a robust Huber loss for both the data and the regularizer, minimized within a convex optimization framework. We introduce a novel constraint on the common areas, to bias the solution towards mutually exclusive regions. We also propose a regularization scheme that is adapted to the spatial statistics of the residual at each iteration, resulting in a varying degree of regularization being applied as the algorithm proceeds: the effect of the regularizer is strongest at initialization, and wanes as the solution increasingly fits the data. This minimizes the bias induced by the regularizer at convergence. We design an efficient convex optimization algorithm based on the alternating direction method of multipliers using the equivalent relation between the Huber function and the proximal operator of the one-norm. We empirically validate our proposed algorithm on synthetic and real images and offer an information-theoretic derivation of the cost-function that highlights the modeling choices made.

Coarse-to-Fine Segmentation With Shape-Tailored Scale Spaces

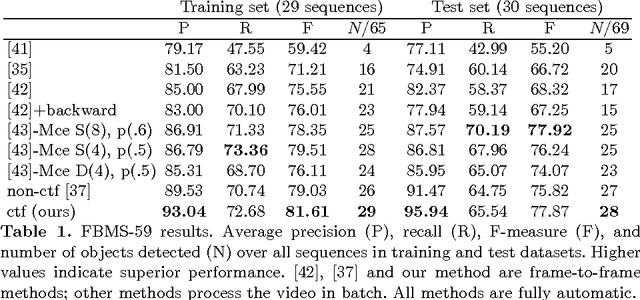
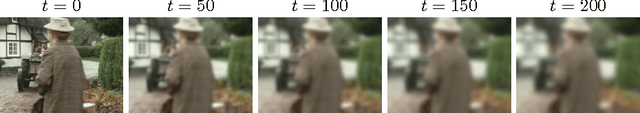
We formulate a general energy and method for segmentation that is designed to have preference for segmenting the coarse structure over the fine structure of the data, without smoothing across boundaries of regions. The energy is formulated by considering data terms at a continuum of scales from the scale space computed from the Heat Equation within regions, and integrating these terms over all time. We show that the energy may be approximately optimized without solving for the entire scale space, but rather solving time-independent linear equations at the native scale of the image, making the method computationally feasible. We provide a multi-region scheme, and apply our method to motion segmentation. Experiments on a benchmark dataset shows that our method is less sensitive to clutter or other undesirable fine-scale structure, and leads to better performance in motion segmentation.

Tracking via Motion Estimation with Physically Motivated Inter-Region Constraints

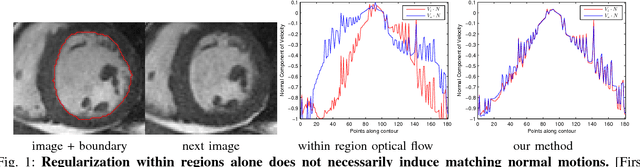
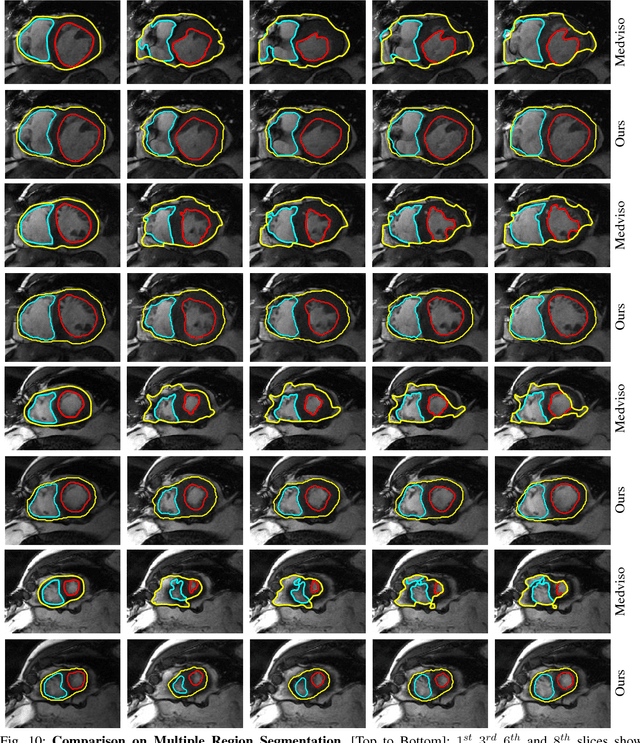
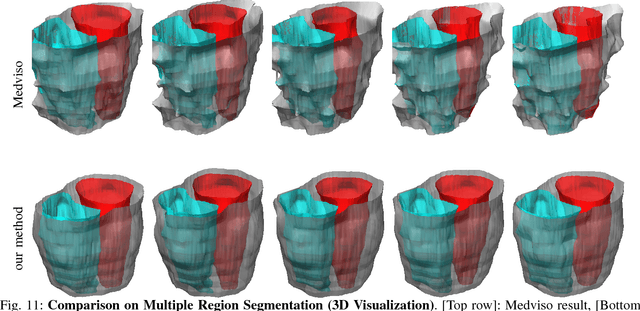
In this paper, we propose a method for tracking structures (e.g., ventricles and myocardium) in cardiac images (e.g., magnetic resonance) by propagating forward in time a previous estimate of the structures via a new deformation estimation scheme that is motivated by physical constraints of fluid motion. The method employs within structure motion estimation (so that differing motions among different structures are not mixed) while simultaneously satisfying the physical constraint in fluid motion that at the interface between a fluid and a medium, the normal component of the fluid's motion must match the normal component of the motion of the medium. We show how to estimate the motion according to the previous considerations in a variational framework, and in particular, show that these conditions lead to PDEs with boundary conditions at the interface that resemble Robin boundary conditions and induce coupling between structures. We illustrate the use of this motion estimation scheme in propagating a segmentation across frames and show that it leads to more accurate segmentation than traditional motion estimation that does not make use of physical constraints. Further, the method is naturally suited to interactive segmentation methods, which are prominently used in practice in commercial applications for cardiac analysis, where typically a segmentation from the previous frame is used to predict a segmentation in the next frame. We show that our propagation scheme reduces the amount of user interaction by predicting more accurate segmentations than commonly used and recent interactive commercial techniques.