SPDEBench: An Extensive Benchmark for Learning Regular and Singular Stochastic PDEs

Stochastic Partial Differential Equations (SPDEs) driven by random noise play a central role in modelling physical processes whose spatio-temporal dynamics can be rough, such as turbulence flows, superconductors, and quantum dynamics. To efficiently model these processes and make predictions, machine learning (ML)-based surrogate models are proposed, with their network architectures incorporating the spatio-temporal roughness in their design. However, it lacks an extensive and unified datasets for SPDE learning; especially, existing datasets do not account for the computational error introduced by noise sampling and the necessary renormalization required for handling singular SPDEs. We thus introduce SPDEBench, which is designed to solve typical SPDEs of physical significance (e.g., the $\Phi^4_d$, wave, incompressible Navier--Stokes, and KdV equations) on 1D or 2D tori driven by white noise via ML methods. New datasets for singular SPDEs based on the renormalization process have been constructed, and novel ML models achieving the best results to date have been proposed. In particular, we investigate the impact of computational error introduced by noise sampling and renormalization on the performance comparison of ML models and highlight the importance of selecting high-quality test data for accurate evaluation. Results are benchmarked with traditional numerical solvers and ML-based models, including FNO, NSPDE and DLR-Net, etc. It is shown that, for singular SPDEs, naively applying ML models on data without specifying the numerical schemes can lead to significant errors and misleading conclusions. Our SPDEBench provides an open-source codebase that ensures full reproducibility of benchmarking across a variety of SPDE datasets while offering the flexibility to incorporate new datasets and machine learning baselines, making it a valuable resource for the community.

Riemannian Neural Geodesic Interpolant

Stochastic interpolants are efficient generative models that bridge two arbitrary probability density functions in finite time, enabling flexible generation from the source to the target distribution or vice versa. These models are primarily developed in Euclidean space, and are therefore limited in their application to many distribution learning problems defined on Riemannian manifolds in real-world scenarios. In this work, we introduce the Riemannian Neural Geodesic Interpolant (RNGI) model, which interpolates between two probability densities on a Riemannian manifold along the stochastic geodesics, and then samples from one endpoint as the final state using the continuous flow originating from the other endpoint. We prove that the temporal marginal density of RNGI solves a transport equation on the Riemannian manifold. After training the model's the neural velocity and score fields, we propose the Embedding Stochastic Differential Equation (E-SDE) algorithm for stochastic sampling of RNGI. E-SDE significantly improves the sampling quality by reducing the accumulated error caused by the excessive intrinsic discretization of Riemannian Brownian motion in the classical Geodesic Random Walk (GRW) algorithm. We also provide theoretical bounds on the generative bias measured in terms of KL-divergence. Finally, we demonstrate the effectiveness of the proposed RNGI and E-SDE through experiments conducted on both collected and synthetic distributions on S2 and SO(3).

Deep Random Vortex Method for Simulation and Inference of Navier-Stokes Equations

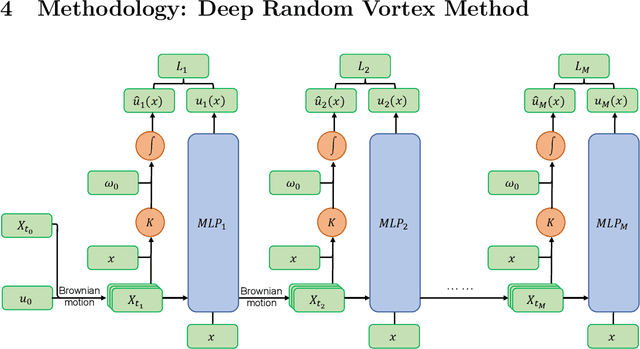
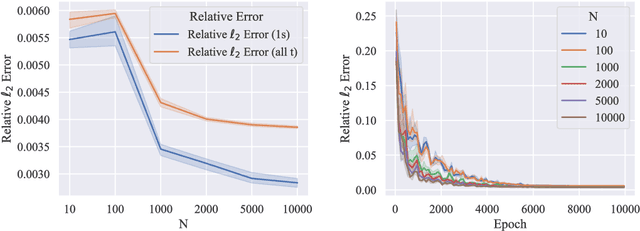
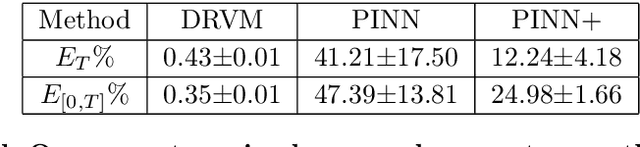
Navier-Stokes equations are significant partial differential equations that describe the motion of fluids such as liquids and air. Due to the importance of Navier-Stokes equations, the development on efficient numerical schemes is important for both science and engineer. Recently, with the development of AI techniques, several approaches have been designed to integrate deep neural networks in simulating and inferring the fluid dynamics governed by incompressible Navier-Stokes equations, which can accelerate the simulation or inferring process in a mesh-free and differentiable way. In this paper, we point out that the capability of existing deep Navier-Stokes informed methods is limited to handle non-smooth or fractional equations, which are two critical situations in reality. To this end, we propose the \emph{Deep Random Vortex Method} (DRVM), which combines the neural network with a random vortex dynamics system equivalent to the Navier-Stokes equation. Specifically, the random vortex dynamics motivates a Monte Carlo based loss function for training the neural network, which avoids the calculation of derivatives through auto-differentiation. Therefore, DRVM not only can efficiently solve Navier-Stokes equations involving rough path, non-differentiable initial conditions and fractional operators, but also inherits the mesh-free and differentiable benefits of the deep-learning-based solver. We conduct experiments on the Cauchy problem, parametric solver learning, and the inverse problem of both 2-d and 3-d incompressible Navier-Stokes equations. The proposed method achieves accurate results for simulation and inference of Navier-Stokes equations. Especially for the cases that include singular initial conditions, DRVM significantly outperforms existing PINN method.

Neural Operator with Regularity Structure for Modeling Dynamics Driven by SPDEs

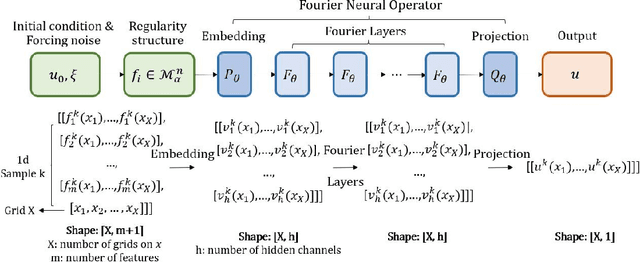
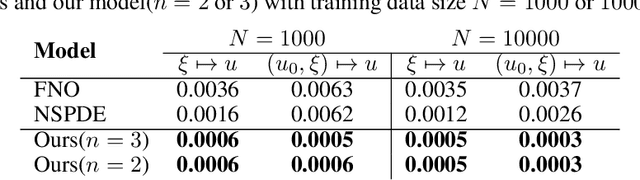
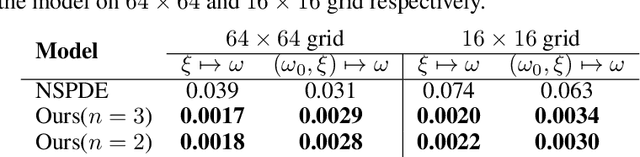
Stochastic partial differential equations (SPDEs) are significant tools for modeling dynamics in many areas including atmospheric sciences and physics. Neural Operators, generations of neural networks with capability of learning maps between infinite-dimensional spaces, are strong tools for solving parametric PDEs. However, they lack the ability to modeling SPDEs which usually have poor regularity due to the driving noise. As the theory of regularity structure has achieved great successes in analyzing SPDEs and provides the concept model feature vectors that well-approximate SPDEs' solutions, we propose the Neural Operator with Regularity Structure (NORS) which incorporates the feature vectors for modeling dynamics driven by SPDEs. We conduct experiments on various of SPDEs including the dynamic Phi41 model and the 2d stochastic Navier-Stokes equation, and the results demonstrate that the NORS is resolution-invariant, efficient, and achieves one order of magnitude lower error with a modest amount of data.