SPDEBench: An Extensive Benchmark for Learning Regular and Singular Stochastic PDEs

Stochastic Partial Differential Equations (SPDEs) driven by random noise play a central role in modelling physical processes whose spatio-temporal dynamics can be rough, such as turbulence flows, superconductors, and quantum dynamics. To efficiently model these processes and make predictions, machine learning (ML)-based surrogate models are proposed, with their network architectures incorporating the spatio-temporal roughness in their design. However, it lacks an extensive and unified datasets for SPDE learning; especially, existing datasets do not account for the computational error introduced by noise sampling and the necessary renormalization required for handling singular SPDEs. We thus introduce SPDEBench, which is designed to solve typical SPDEs of physical significance (e.g., the $\Phi^4_d$, wave, incompressible Navier--Stokes, and KdV equations) on 1D or 2D tori driven by white noise via ML methods. New datasets for singular SPDEs based on the renormalization process have been constructed, and novel ML models achieving the best results to date have been proposed. In particular, we investigate the impact of computational error introduced by noise sampling and renormalization on the performance comparison of ML models and highlight the importance of selecting high-quality test data for accurate evaluation. Results are benchmarked with traditional numerical solvers and ML-based models, including FNO, NSPDE and DLR-Net, etc. It is shown that, for singular SPDEs, naively applying ML models on data without specifying the numerical schemes can lead to significant errors and misleading conclusions. Our SPDEBench provides an open-source codebase that ensures full reproducibility of benchmarking across a variety of SPDE datasets while offering the flexibility to incorporate new datasets and machine learning baselines, making it a valuable resource for the community.

GarmageNet: A Dataset and Scalable Representation for Generic Garment Modeling

High-fidelity garment modeling remains challenging due to the lack of large-scale, high-quality datasets and efficient representations capable of handling non-watertight, multi-layer geometries. In this work, we introduce Garmage, a neural-network-and-CG-friendly garment representation that seamlessly encodes the accurate geometry and sewing pattern of complex multi-layered garments as a structured set of per-panel geometry images. As a dual-2D-3D representation, Garmage achieves an unprecedented integration of 2D image-based algorithms with 3D modeling workflows, enabling high fidelity, non-watertight, multi-layered garment geometries with direct compatibility for industrial-grade simulations.Built upon this representation, we present GarmageNet, a novel generation framework capable of producing detailed multi-layered garments with body-conforming initial geometries and intricate sewing patterns, based on user prompts or existing in-the-wild sewing patterns. Furthermore, we introduce a robust stitching algorithm that recovers per-vertex stitches, ensuring seamless integration into flexible simulation pipelines for downstream editing of sewing patterns, material properties, and dynamic simulations. Finally, we release an industrial-standard, large-scale, high-fidelity garment dataset featuring detailed annotations, vertex-wise correspondences, and a robust pipeline for converting unstructured production sewing patterns into GarmageNet standard structural assets, paving the way for large-scale, industrial-grade garment generation systems.

Enhancing Retrieval-Augmented Generation: A Study of Best Practices

Retrieval-Augmented Generation (RAG) systems have recently shown remarkable advancements by integrating retrieval mechanisms into language models, enhancing their ability to produce more accurate and contextually relevant responses. However, the influence of various components and configurations within RAG systems remains underexplored. A comprehensive understanding of these elements is essential for tailoring RAG systems to complex retrieval tasks and ensuring optimal performance across diverse applications. In this paper, we develop several advanced RAG system designs that incorporate query expansion, various novel retrieval strategies, and a novel Contrastive In-Context Learning RAG. Our study systematically investigates key factors, including language model size, prompt design, document chunk size, knowledge base size, retrieval stride, query expansion techniques, Contrastive In-Context Learning knowledge bases, multilingual knowledge bases, and Focus Mode retrieving relevant context at sentence-level. Through extensive experimentation, we provide a detailed analysis of how these factors influence response quality. Our findings offer actionable insights for developing RAG systems, striking a balance between contextual richness and retrieval-generation efficiency, thereby paving the way for more adaptable and high-performing RAG frameworks in diverse real-world scenarios. Our code and implementation details are publicly available.

PCF-GAN: generating sequential data via the characteristic function of measures on the path space

Generating high-fidelity time series data using generative adversarial networks (GANs) remains a challenging task, as it is difficult to capture the temporal dependence of joint probability distributions induced by time-series data. Towards this goal, a key step is the development of an effective discriminator to distinguish between time series distributions. We propose the so-called PCF-GAN, a novel GAN that incorporates the path characteristic function (PCF) as the principled representation of time series distribution into the discriminator to enhance its generative performance. On the one hand, we establish theoretical foundations of the PCF distance by proving its characteristicity, boundedness, differentiability with respect to generator parameters, and weak continuity, which ensure the stability and feasibility of training the PCF-GAN. On the other hand, we design efficient initialisation and optimisation schemes for PCFs to strengthen the discriminative power and accelerate training efficiency. To further boost the capabilities of complex time series generation, we integrate the auto-encoder structure via sequential embedding into the PCF-GAN, which provides additional reconstruction functionality. Extensive numerical experiments on various datasets demonstrate the consistently superior performance of PCF-GAN over state-of-the-art baselines, in both generation and reconstruction quality. Code is available at https://github.com/DeepIntoStreams/PCF-GAN.

Gaussian kernels on non-simply-connected closed Riemannian manifolds are never positive definite

We show that the Gaussian kernel $\exp\left\{-\lambda d_g^2(\bullet, \bullet)\right\}$ on any non-simply-connected closed Riemannian manifold $(\mathcal{M},g)$, where $d_g$ is the geodesic distance, is not positive definite for any $\lambda > 0$, combining analyses in the recent preprint~[9] by Da Costa--Mostajeran--Ortega and classical comparison theorems in Riemannian geometry.

Path Development Network with Finite-dimensional Lie Group Representation

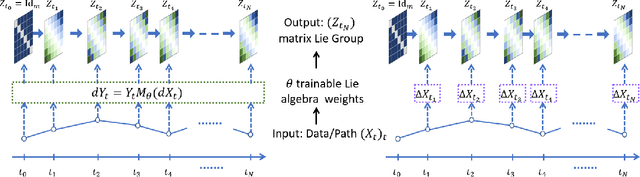
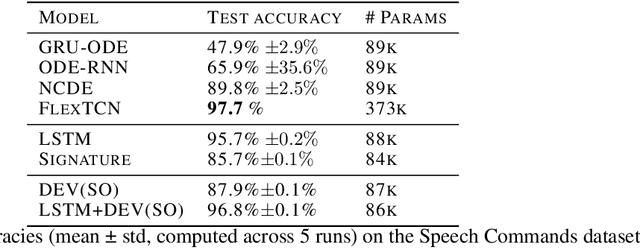
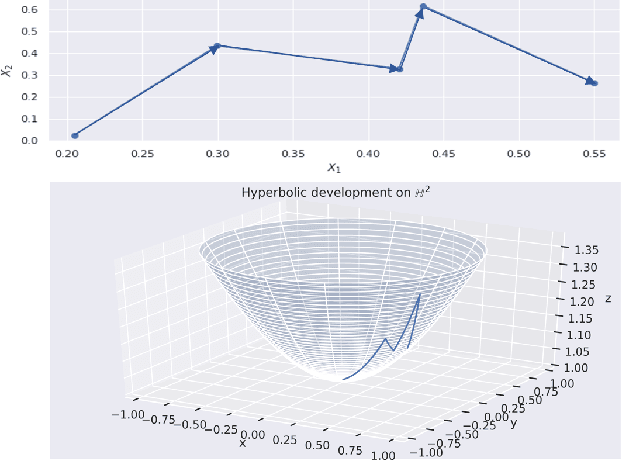
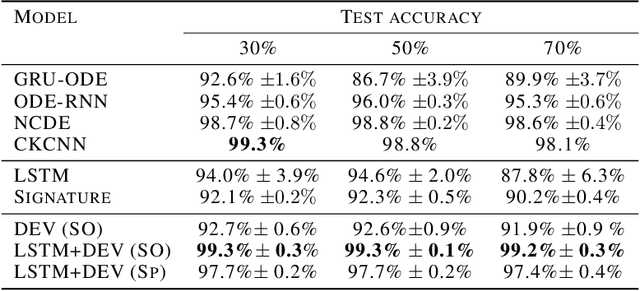
The path signature, a mathematically principled and universal feature of sequential data, leads to a performance boost of deep learning-based models in various sequential data tasks as a complimentary feature. However, it suffers from the curse of dimensionality when the path dimension is high. To tackle this problem, we propose a novel, trainable path development layer, which exploits representations of sequential data with the help of finite-dimensional matrix Lie groups. We also design the backpropagation algorithm of the development layer via an optimisation method on manifolds known as trivialisation. Numerical experiments demonstrate that the path development consistently and significantly outperforms, in terms of accuracy and dimensionality, signature features on several empirical datasets. Moreover, stacking the LSTM with the development layer with a suitable matrix Lie group is empirically proven to alleviate the gradient issues of LSTMs and the resulting hybrid model achieves the state-of-the-art performance.