An Empirical Analysis of the Advantages of Finite- v.s. Infinite-Width Bayesian Neural Networks

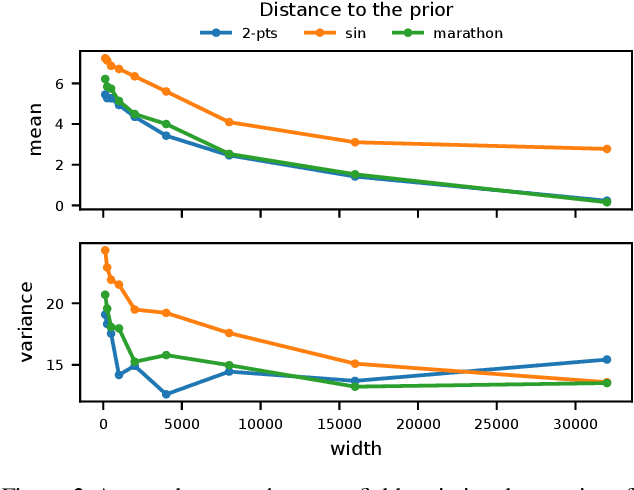
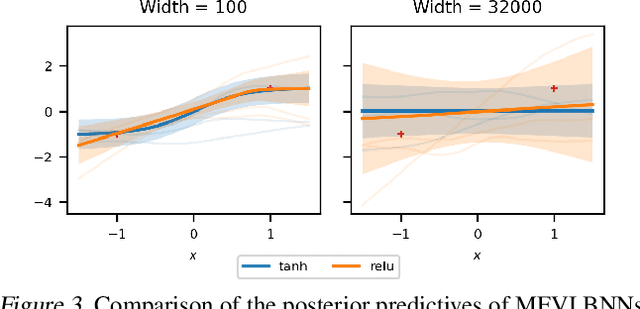
Comparing Bayesian neural networks (BNNs) with different widths is challenging because, as the width increases, multiple model properties change simultaneously, and, inference in the finite-width case is intractable. In this work, we empirically compare finite- and infinite-width BNNs, and provide quantitative and qualitative explanations for their performance difference. We find that when the model is mis-specified, increasing width can hurt BNN performance. In these cases, we provide evidence that finite-width BNNs generalize better partially due to the properties of their frequency spectrum that allows them to adapt under model mismatch.

Towards a Unified Framework for Uncertainty-aware Nonlinear Variable Selection with Theoretical Guarantees

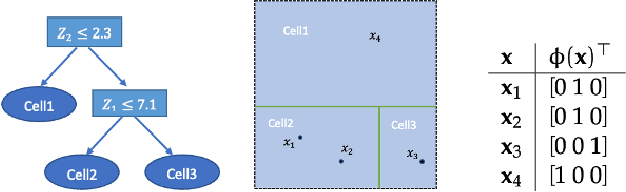
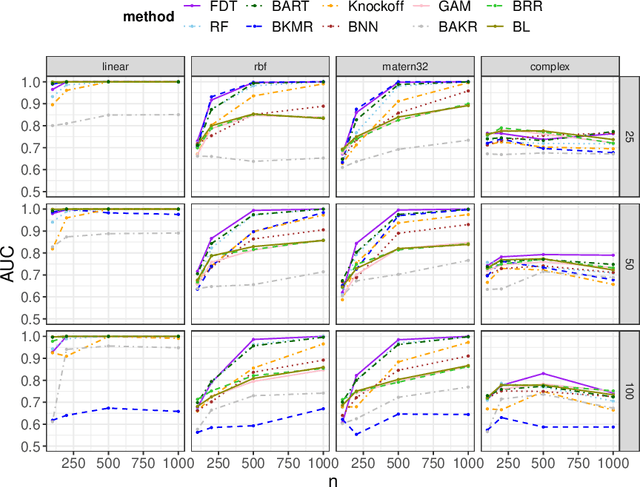
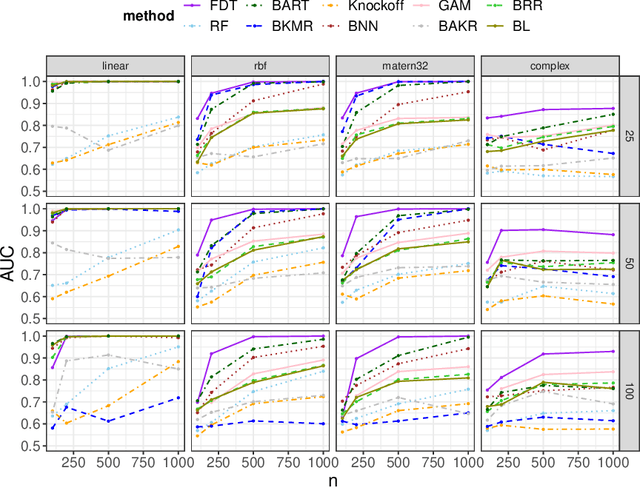
We develop a simple and unified framework for nonlinear variable selection that incorporates model uncertainty and is compatible with a wide range of machine learning models (e.g., tree ensembles, kernel methods and neural network). In particular, for a learned nonlinear model $f(\mathbf{x})$, we consider quantifying the importance of an input variable $\mathbf{x}^j$ using the integrated gradient measure $\psi_j = \Vert \frac{\partial}{\partial \mathbf{x}^j} f(\mathbf{x})\Vert^2_2$. We then (1) provide a principled approach for quantifying variable selection uncertainty by deriving its posterior distribution, and (2) show that the approach is generalizable even to non-differentiable models such as tree ensembles. Rigorous Bayesian nonparametric theorems are derived to guarantee the posterior consistency and asymptotic uncertainty of the proposed approach. Extensive simulation confirms that the proposed algorithm outperforms existing classic and recent variable selection methods.

Wide Mean-Field Bayesian Neural Networks Ignore the Data

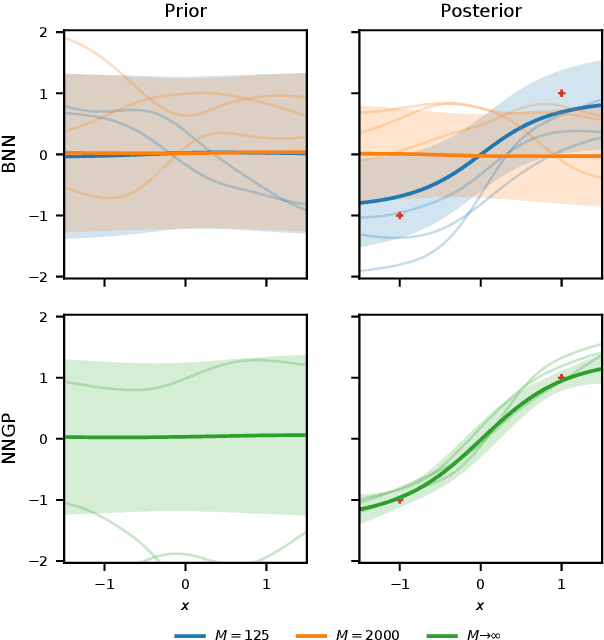
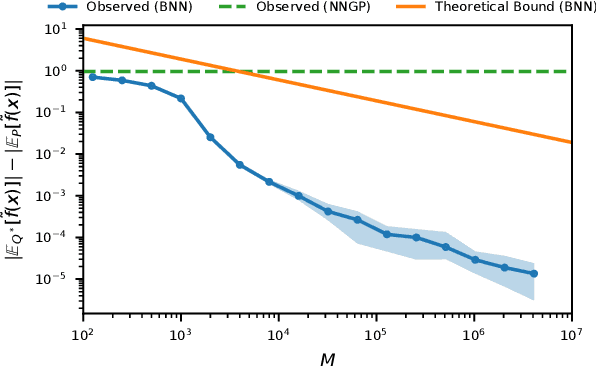
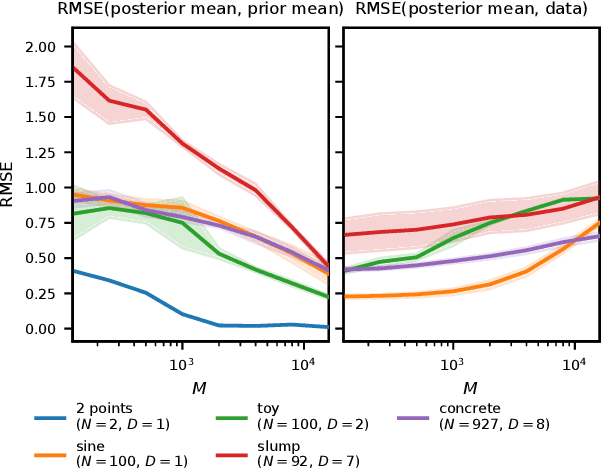
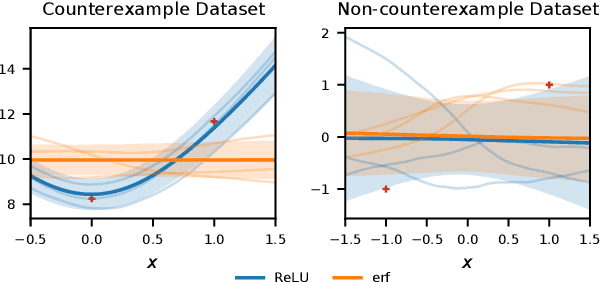
Bayesian neural networks (BNNs) combine the expressive power of deep learning with the advantages of Bayesian formalism. In recent years, the analysis of wide, deep BNNs has provided theoretical insight into their priors and posteriors. However, we have no analogous insight into their posteriors under approximate inference. In this work, we show that mean-field variational inference entirely fails to model the data when the network width is large and the activation function is odd. Specifically, for fully-connected BNNs with odd activation functions and a homoscedastic Gaussian likelihood, we show that the optimal mean-field variational posterior predictive (i.e., function space) distribution converges to the prior predictive distribution as the width tends to infinity. We generalize aspects of this result to other likelihoods. Our theoretical results are suggestive of underfitting behavior previously observered in BNNs. While our convergence bounds are non-asymptotic and constants in our analysis can be computed, they are currently too loose to be applicable in standard training regimes. Finally, we show that the optimal approximate posterior need not tend to the prior if the activation function is not odd, showing that our statements cannot be generalized arbitrarily.

Wide Mean-Field Variational Bayesian Neural Networks Ignore the Data

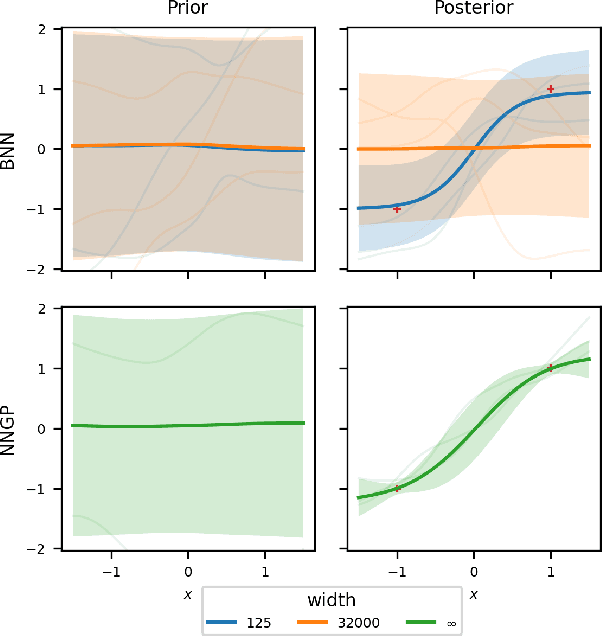
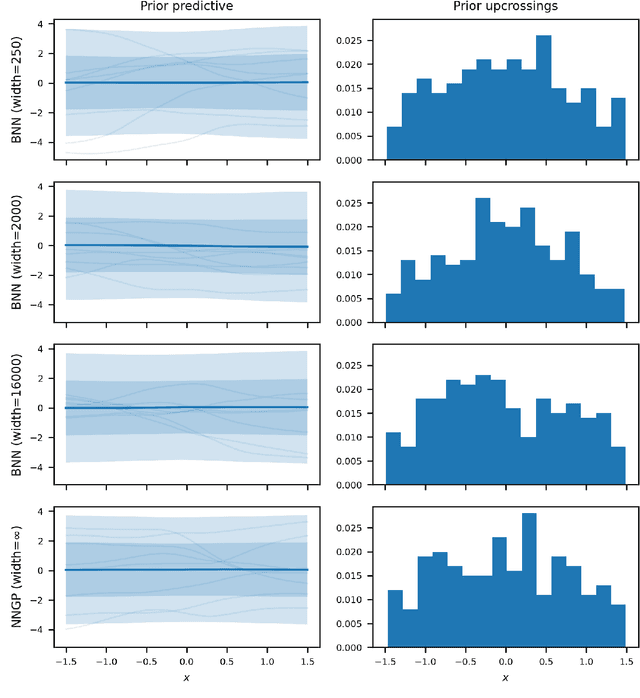
Variational inference enables approximate posterior inference of the highly over-parameterized neural networks that are popular in modern machine learning. Unfortunately, such posteriors are known to exhibit various pathological behaviors. We prove that as the number of hidden units in a single-layer Bayesian neural network tends to infinity, the function-space posterior mean under mean-field variational inference actually converges to zero, completely ignoring the data. This is in contrast to the true posterior, which converges to a Gaussian process. Our work provides insight into the over-regularization of the KL divergence in variational inference.

Towards Expressive Priors for Bayesian Neural Networks: Poisson Process Radial Basis Function Networks

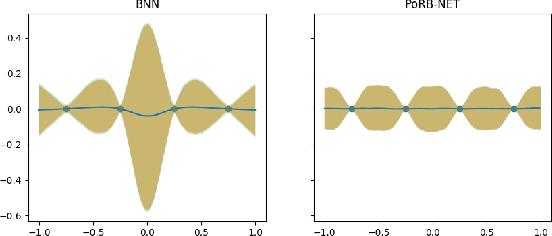
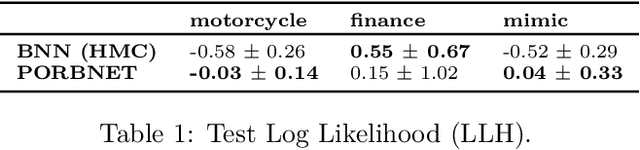
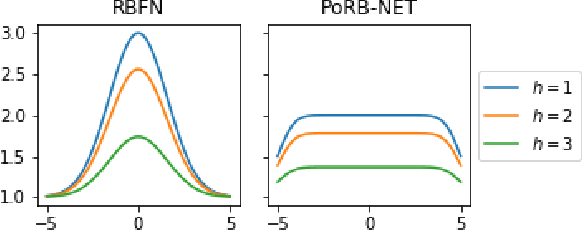
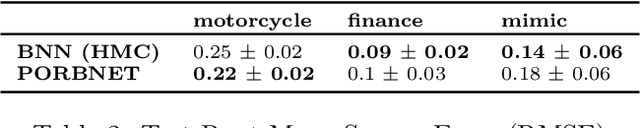
While Bayesian neural networks have many appealing characteristics, current priors do not easily allow users to specify basic properties such as expected lengthscale or amplitude variance. In this work, we introduce Poisson Process Radial Basis Function Networks, a novel prior that is able to encode amplitude stationarity and input-dependent lengthscale. We prove that our novel formulation allows for a decoupled specification of these properties, and that the estimated regression function is consistent as the number of observations tends to infinity. We demonstrate its behavior on synthetic and real examples.

Learning a Generative Model of Cancer Metastasis

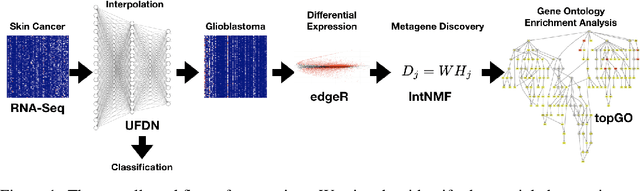
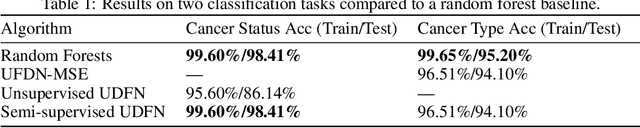
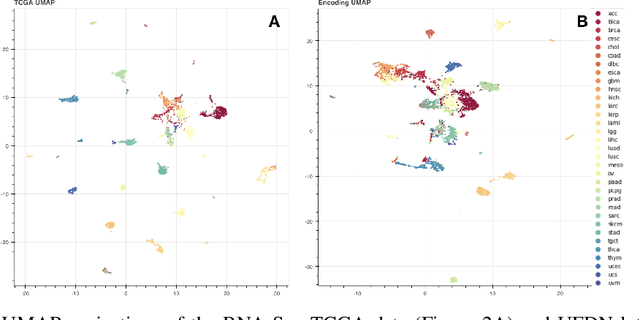
We introduce a Unified Disentanglement Network (UFDN) trained on The Cancer Genome Atlas (TCGA). We demonstrate that the UFDN learns a biologically relevant latent space of gene expression data by applying our network to two classification tasks of cancer status and cancer type. Our UFDN specific algorithms perform comparably to random forest methods. The UFDN allows for continuous, partial interpolation between distinct cancer types. Furthermore, we perform an analysis of differentially expressed genes between skin cutaneous melanoma(SKCM) samples and the same samples interpolated into glioblastoma (GBM). We demonstrate that our interpolations learn relevant metagenes that recapitulate known glioblastoma mechanisms and suggest possible starting points for investigations into the metastasis of SKCM into GBM.

A Theory of Statistical Inference for Ensuring the Robustness of Scientific Results

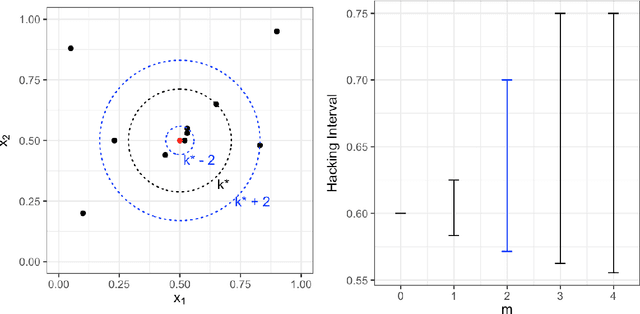
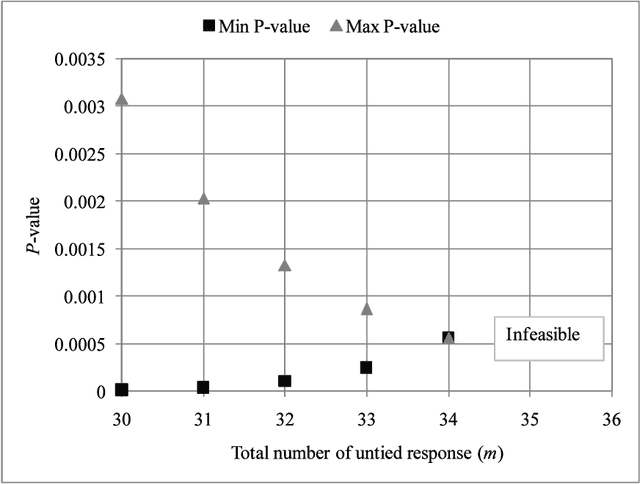
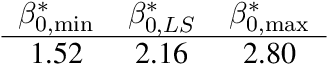
Inference is the process of using facts we know to learn about facts we do not know. A theory of inference gives assumptions necessary to get from the former to the latter, along with a definition for and summary of the resulting uncertainty. Any one theory of inference is neither right nor wrong, but merely an axiom that may or may not be useful. Each of the many diverse theories of inference can be valuable for certain applications. However, no existing theory of inference addresses the tendency to choose, from the range of plausible data analysis specifications consistent with prior evidence, those that inadvertently favor one's own hypotheses. Since the biases from these choices are a growing concern across scientific fields, and in a sense the reason the scientific community was invented in the first place, we introduce a new theory of inference designed to address this critical problem. We derive "hacking intervals," which are the range of a summary statistic one may obtain given a class of possible endogenous manipulations of the data. Hacking intervals require no appeal to hypothetical data sets drawn from imaginary superpopulations. A scientific result with a small hacking interval is more robust to researcher manipulation than one with a larger interval, and is often easier to interpret than a classical confidence interval. Some versions of hacking intervals turn out to be equivalent to classical confidence intervals, which means they may also provide a more intuitive and potentially more useful interpretation of classical confidence intervals