Conformal prediction for full and sparse polynomial chaos expansions

Polynomial Chaos Expansions (PCEs) are widely recognized for their efficient computational performance in surrogate modeling. Yet, a robust framework to quantify local model errors is still lacking. While the local uncertainty of PCE prediction can be captured using bootstrap resampling, other methods offering more rigorous statistical guarantees are needed, especially in the context of small training datasets. Recently, conformal predictions have demonstrated strong potential in machine learning, providing statistically robust and model-agnostic prediction intervals. Due to its generality and versatility, conformal prediction is especially valuable, as it can be adapted to suit a variety of problems, making it a compelling choice for PCE-based surrogate models. In this contribution, we explore its application to PCE-based surrogate models. More precisely, we present the integration of two conformal prediction methods, namely the full conformal and the Jackknife+ approaches, into both full and sparse PCEs. For full PCEs, we introduce computational shortcuts inspired by the inherent structure of regression methods to optimize the implementation of both conformal methods. For sparse PCEs, we incorporate the two approaches with appropriate modifications to the inference strategy, thereby circumventing the non-symmetrical nature of the regression algorithm and ensuring valid prediction intervals. Our developments yield better-calibrated prediction intervals for both full and sparse PCEs, achieving superior coverage over existing approaches, such as the bootstrap, while maintaining a moderate computational cost.

mNARX+: A surrogate model for complex dynamical systems using manifold-NARX and automatic feature selection

We propose an automatic approach for manifold nonlinear autoregressive with exogenous inputs (mNARX) modeling that leverages the feature-based structure of functional-NARX (F-NARX) modeling. This novel approach, termed mNARX+, preserves the key strength of the mNARX framework, which is its expressivity allowing it to model complex dynamical systems, while simultaneously addressing a key limitation: the heavy reliance on domain expertise to identify relevant auxiliary quantities and their causal ordering. Our method employs a data-driven, recursive algorithm that automates the construction of the mNARX model sequence. It operates by sequentially selecting temporal features based on their correlation with the model prediction residuals, thereby automatically identifying the most critical auxiliary quantities and the order in which they should be modeled. This procedure significantly reduces the need for prior system knowledge. We demonstrate the effectiveness of the mNARX+ algorithm on two case studies: a Bouc-Wen oscillator with strong hysteresis and a complex aero-servo-elastic wind turbine simulator. The results show that the algorithm provides a systematic, data-driven method for creating accurate and stable surrogate models for complex dynamical systems.

Surrogate modeling for uncertainty quantification in nonlinear dynamics

Predicting the behavior of complex systems in engineering often involves significant uncertainty about operating conditions, such as external loads, environmental effects, and manufacturing variability. As a result, uncertainty quantification (UQ) has become a critical tool in modeling-based engineering, providing methods to identify, characterize, and propagate uncertainty through computational models. However, the stochastic nature of UQ typically requires numerous evaluations of these models, which can be computationally expensive and limit the scope of feasible analyses. To address this, surrogate models, i.e., efficient functional approximations trained on a limited set of simulations, have become central in modern UQ practice. This book chapter presents a concise review of surrogate modeling techniques for UQ, with a focus on the particularly challenging task of capturing the full time-dependent response of dynamical systems. It introduces a classification of time-dependent problems based on the complexity of input excitation and discusses corresponding surrogate approaches, including combinations of principal component analysis with polynomial chaos expansions, time warping techniques, and nonlinear autoregressive models with exogenous inputs (NARX models). Each method is illustrated with simple application examples to clarify the underlying ideas and practical use.

Learning non-stationary and discontinuous functions using clustering, classification and Gaussian process modelling

Surrogate models have shown to be an extremely efficient aid in solving engineering problems that require repeated evaluations of an expensive computational model. They are built by sparsely evaluating the costly original model and have provided a way to solve otherwise intractable problems. A crucial aspect in surrogate modelling is the assumption of smoothness and regularity of the model to approximate. This assumption is however not always met in reality. For instance in civil or mechanical engineering, some models may present discontinuities or non-smoothness, e.g., in case of instability patterns such as buckling or snap-through. Building a single surrogate model capable of accounting for these fundamentally different behaviors or discontinuities is not an easy task. In this paper, we propose a three-stage approach for the approximation of non-smooth functions which combines clustering, classification and regression. The idea is to split the space following the localized behaviors or regimes of the system and build local surrogates that are eventually assembled. A sequence of well-known machine learning techniques are used: Dirichlet process mixtures models (DPMM), support vector machines and Gaussian process modelling. The approach is tested and validated on two analytical functions and a finite element model of a tensile membrane structure.

Multi-objective robust optimization using adaptive surrogate models for problems with mixed continuous-categorical parameters

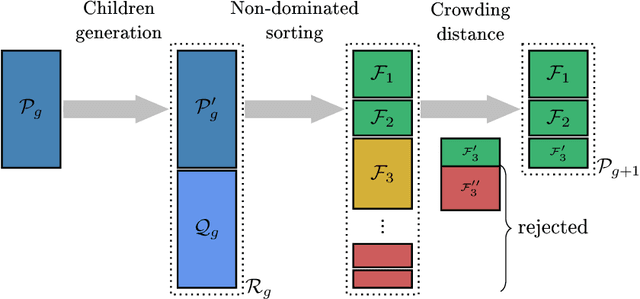
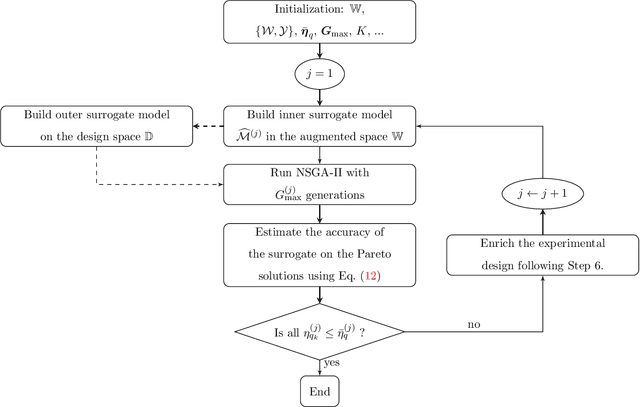
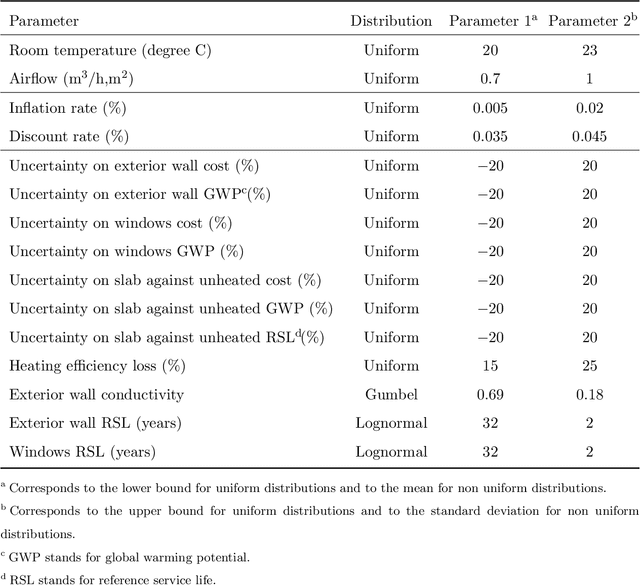
Explicitly accounting for uncertainties is paramount to the safety of engineering structures. Optimization which is often carried out at the early stage of the structural design offers an ideal framework for this task. When the uncertainties are mainly affecting the objective function, robust design optimization is traditionally considered. This work further assumes the existence of multiple and competing objective functions that need to be dealt with simultaneously. The optimization problem is formulated by considering quantiles of the objective functions which allows for the combination of both optimality and robustness in a single metric. By introducing the concept of common random numbers, the resulting nested optimization problem may be solved using a general-purpose solver, herein the non-dominated sorting genetic algorithm (NSGA-II). The computational cost of such an approach is however a serious hurdle to its application in real-world problems. We therefore propose a surrogate-assisted approach using Kriging as an inexpensive approximation of the associated computational model. The proposed approach consists of sequentially carrying out NSGA-II while using an adaptively built Kriging model to estimate of the quantiles. Finally, the methodology is adapted to account for mixed categorical-continuous parameters as the applications involve the selection of qualitative design parameters as well. The methodology is first applied to two analytical examples showing its efficiency. The third application relates to the selection of optimal renovation scenarios of a building considering both its life cycle cost and environmental impact. It shows that when it comes to renovation, the heating system replacement should be the priority.

Rare event estimation using stochastic spectral embedding

Estimating the probability of rare failure events is an essential step in the reliability assessment of engineering systems. Computing this failure probability for complex non-linear systems is challenging, and has recently spurred the development of active-learning reliability methods. These methods approximate the limit-state function (LSF) using surrogate models trained with a sequentially enriched set of model evaluations. A recently proposed method called stochastic spectral embedding (SSE) aims to improve the local approximation accuracy of global, spectral surrogate modelling techniques by sequentially embedding local residual expansions in subdomains of the input space. In this work we apply SSE to the LSF, giving rise to a stochastic spectral embedding-based reliability (SSER) method. The resulting partition of the input space decomposes the failure probability into a set of easy-to-compute domain-wise failure probabilities. We propose a set of modifications that tailor the algorithm to efficiently solve rare event estimation problems. These modifications include specialized refinement domain selection, partitioning and enrichment strategies. We showcase the algorithm performance on four benchmark problems of various dimensionality and complexity in the LSF.

A generalized framework for active learning reliability: survey and benchmark

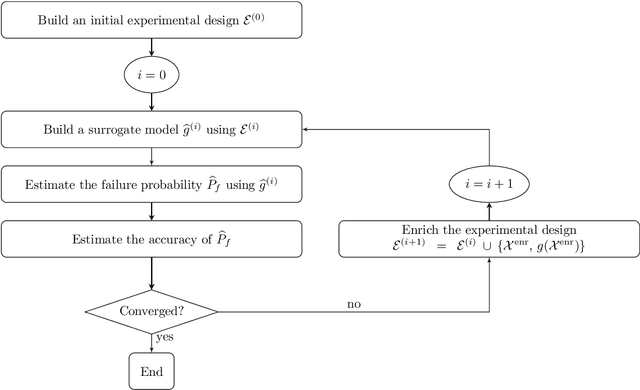
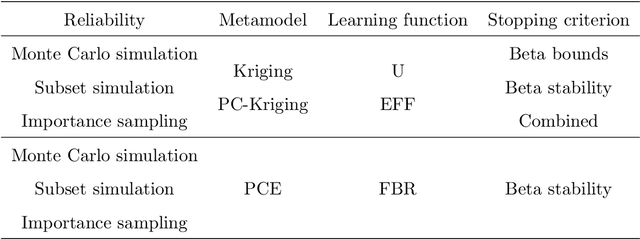
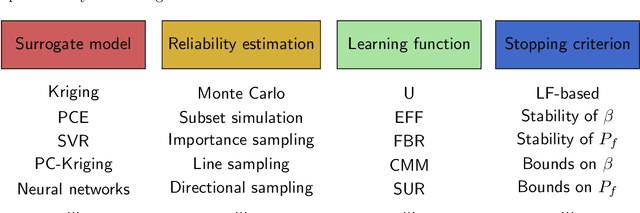
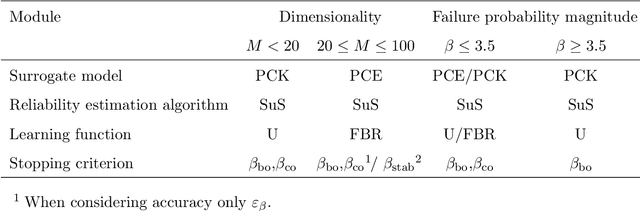
Active learning methods have recently surged in the literature due to their ability to solve complex structural reliability problems within an affordable computational cost. These methods are designed by adaptively building an inexpensive surrogate of the original limit-state function. Examples of such surrogates include Gaussian process models which have been adopted in many contributions, the most popular ones being the efficient global reliability analysis (EGRA) and the active Kriging Monte Carlo simulation (AK-MCS), two milestone contributions in the field. In this paper, we first conduct a survey of the recent literature, showing that most of the proposed methods actually span from modifying one or more aspects of the two aforementioned methods. We then propose a generalized modular framework to build on-the-fly efficient active learning strategies by combining the following four ingredients or modules: surrogate model, reliability estimation algorithm, learning function and stopping criterion. Using this framework, we devise 39 strategies for the solution of 20 reliability benchmark problems. The results of this extensive benchmark are analyzed under various criteria leading to a synthesized set of recommendations for practitioners. These may be refined with a priori knowledge about the feature of the problem to solve, i.e., dimensionality and magnitude of the failure probability. This benchmark has eventually highlighted the importance of using surrogates in conjunction with sophisticated reliability estimation algorithms as a way to enhance the efficiency of the latter.

Global sensitivity analysis for stochastic simulators based on generalized lambda surrogate models

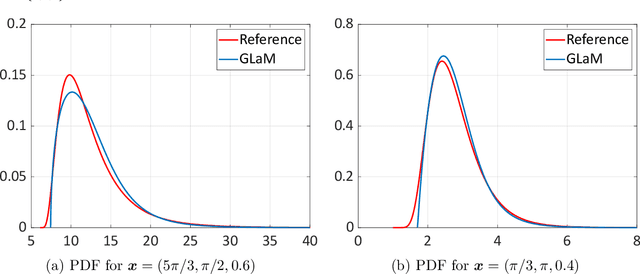
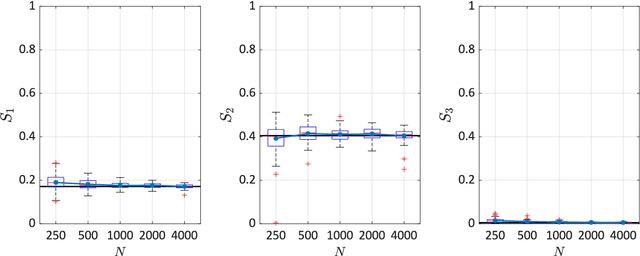
Global sensitivity analysis aims at quantifying the impact of input variability onto the variation of the response of a computational model. It has been widely applied to deterministic simulators, for which a set of input parameters has a unique corresponding output value. Stochastic simulators, however, have intrinsic randomness and give different results when run twice with the same input parameters. Due to this random nature, conventional Sobol' indices can be extended to stochastic simulators in different ways. In this paper, we discuss three possible extensions and focus on those that only depend on the statistical dependence between input and output. This choice ignores the detailed data generating process involving the internal randomness, and can thus be applied to a wider class of problems. We propose to use the generalized lambda model to emulate the response distribution of stochastic simulators. Such a surrogate can be constructed in a non-intrusive manner without the need for replications. The proposed method is applied to three examples including two case studies in finance and epidemiology. The results confirm the convergence of the approach for estimating the sensitivity indices even with the presence of strong heteroscedasticity and small signal-to-noise ratio.

Stochastic spectral embedding

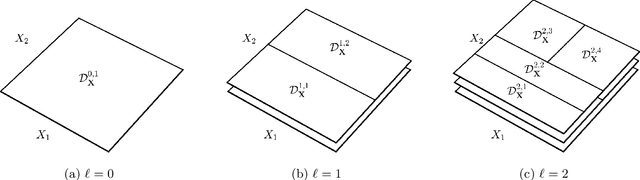
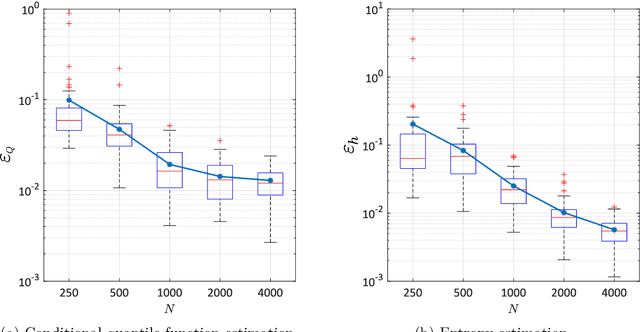
Constructing approximations that can accurately mimic the behaviour of complex models at reduced computational costs is an important aspect of uncertainty quantification. Despite their flexibility and efficiency, classical surrogate models such as Kriging or polynomial chaos expansions tend to struggle with highly non-linear, localized or non-stationary computational models. We hereby propose a novel sequential adaptive surrogate modelling method based on recursively embedding locally spectral expansions. It is achieved by means of disjoint recursive partitioning of the input domain, which consists in sequentially splitting the latter into smaller subdomains, and constructing a simpler local spectral expansions in each, exploiting the trade-off complexity vs. locality. The resulting expansion, which we refer to as "stochastic spectral embedding" (SSE), is a piece-wise continuous approximation of the model response that shows promising approximation capabilities, and good scaling with both the problem dimension and the size of the training set. We finally show how the method compares favourably against state-of-the-art sparse polynomial chaos expansions on a set of models with different complexity and input dimension.

Replication-based emulation of the response distribution of stochastic simulators using generalized lambda distributions

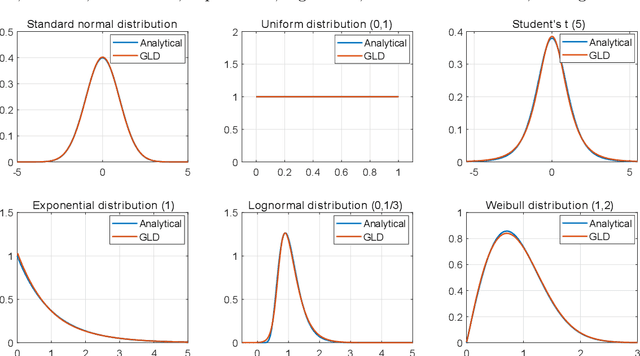
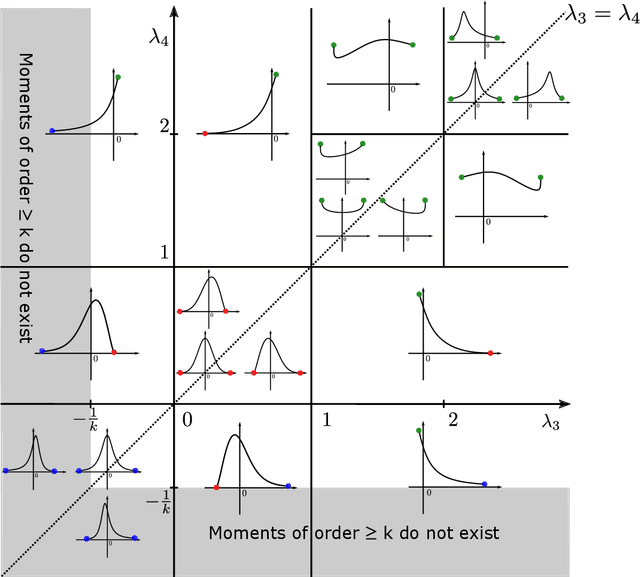
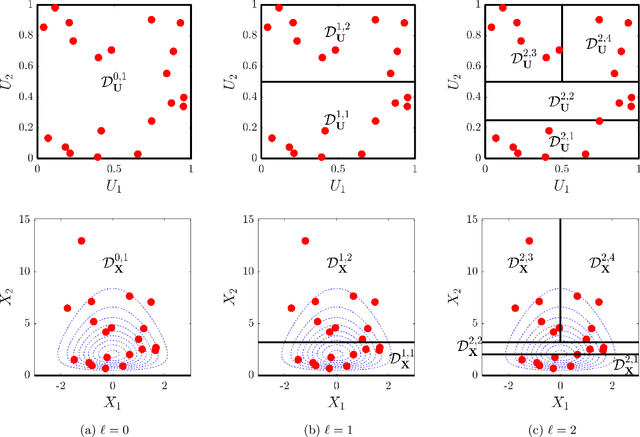
Due to limited computational power, performing uncertainty quantification analyses with complex computational models can be a challenging task. This is exacerbated in the context of stochastic simulators, the response of which to a given set of input parameters, rather than being a deterministic value, is a random variable with unknown probability density function (PDF). Of interest in this paper is the construction of a surrogate that can accurately predict this response PDF for any input parameters. We suggest using a flexible distribution family -- the generalized lambda distribution -- to approximate the response PDF. The associated distribution parameters are cast as functions of input parameters and represented by sparse polynomial chaos expansions. To build such a surrogate model, we propose an approach based on a local inference of the response PDF at each point of the experimental design based on replicated model evaluations. Two versions of this framework are proposed and compared on analytical examples and case studies.