Conformal prediction for full and sparse polynomial chaos expansions

Polynomial Chaos Expansions (PCEs) are widely recognized for their efficient computational performance in surrogate modeling. Yet, a robust framework to quantify local model errors is still lacking. While the local uncertainty of PCE prediction can be captured using bootstrap resampling, other methods offering more rigorous statistical guarantees are needed, especially in the context of small training datasets. Recently, conformal predictions have demonstrated strong potential in machine learning, providing statistically robust and model-agnostic prediction intervals. Due to its generality and versatility, conformal prediction is especially valuable, as it can be adapted to suit a variety of problems, making it a compelling choice for PCE-based surrogate models. In this contribution, we explore its application to PCE-based surrogate models. More precisely, we present the integration of two conformal prediction methods, namely the full conformal and the Jackknife+ approaches, into both full and sparse PCEs. For full PCEs, we introduce computational shortcuts inspired by the inherent structure of regression methods to optimize the implementation of both conformal methods. For sparse PCEs, we incorporate the two approaches with appropriate modifications to the inference strategy, thereby circumventing the non-symmetrical nature of the regression algorithm and ensuring valid prediction intervals. Our developments yield better-calibrated prediction intervals for both full and sparse PCEs, achieving superior coverage over existing approaches, such as the bootstrap, while maintaining a moderate computational cost.

Global sensitivity analysis for stochastic simulators based on generalized lambda surrogate models

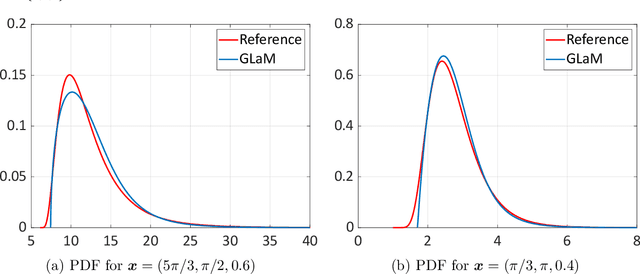
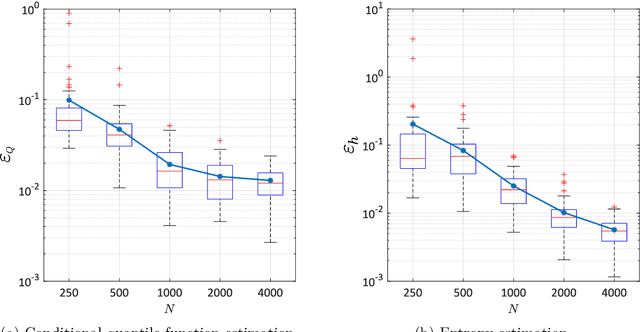
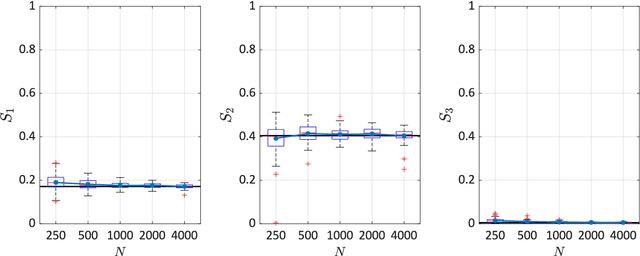
Global sensitivity analysis aims at quantifying the impact of input variability onto the variation of the response of a computational model. It has been widely applied to deterministic simulators, for which a set of input parameters has a unique corresponding output value. Stochastic simulators, however, have intrinsic randomness and give different results when run twice with the same input parameters. Due to this random nature, conventional Sobol' indices can be extended to stochastic simulators in different ways. In this paper, we discuss three possible extensions and focus on those that only depend on the statistical dependence between input and output. This choice ignores the detailed data generating process involving the internal randomness, and can thus be applied to a wider class of problems. We propose to use the generalized lambda model to emulate the response distribution of stochastic simulators. Such a surrogate can be constructed in a non-intrusive manner without the need for replications. The proposed method is applied to three examples including two case studies in finance and epidemiology. The results confirm the convergence of the approach for estimating the sensitivity indices even with the presence of strong heteroscedasticity and small signal-to-noise ratio.

Replication-based emulation of the response distribution of stochastic simulators using generalized lambda distributions

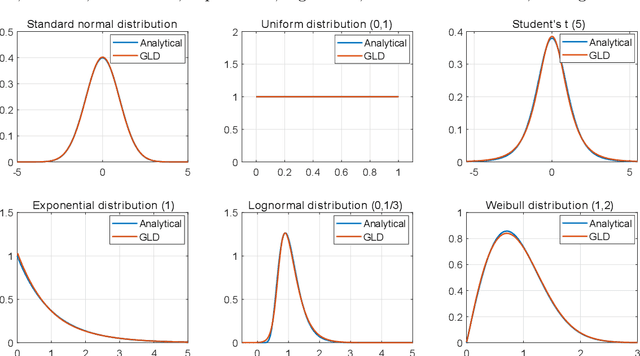
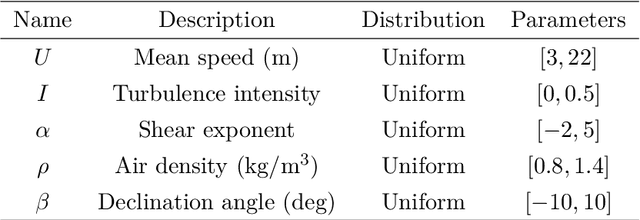
Due to limited computational power, performing uncertainty quantification analyses with complex computational models can be a challenging task. This is exacerbated in the context of stochastic simulators, the response of which to a given set of input parameters, rather than being a deterministic value, is a random variable with unknown probability density function (PDF). Of interest in this paper is the construction of a surrogate that can accurately predict this response PDF for any input parameters. We suggest using a flexible distribution family -- the generalized lambda distribution -- to approximate the response PDF. The associated distribution parameters are cast as functions of input parameters and represented by sparse polynomial chaos expansions. To build such a surrogate model, we propose an approach based on a local inference of the response PDF at each point of the experimental design based on replicated model evaluations. Two versions of this framework are proposed and compared on analytical examples and case studies.