Learning non-stationary and discontinuous functions using clustering, classification and Gaussian process modelling

Surrogate models have shown to be an extremely efficient aid in solving engineering problems that require repeated evaluations of an expensive computational model. They are built by sparsely evaluating the costly original model and have provided a way to solve otherwise intractable problems. A crucial aspect in surrogate modelling is the assumption of smoothness and regularity of the model to approximate. This assumption is however not always met in reality. For instance in civil or mechanical engineering, some models may present discontinuities or non-smoothness, e.g., in case of instability patterns such as buckling or snap-through. Building a single surrogate model capable of accounting for these fundamentally different behaviors or discontinuities is not an easy task. In this paper, we propose a three-stage approach for the approximation of non-smooth functions which combines clustering, classification and regression. The idea is to split the space following the localized behaviors or regimes of the system and build local surrogates that are eventually assembled. A sequence of well-known machine learning techniques are used: Dirichlet process mixtures models (DPMM), support vector machines and Gaussian process modelling. The approach is tested and validated on two analytical functions and a finite element model of a tensile membrane structure.

Multi-objective robust optimization using adaptive surrogate models for problems with mixed continuous-categorical parameters

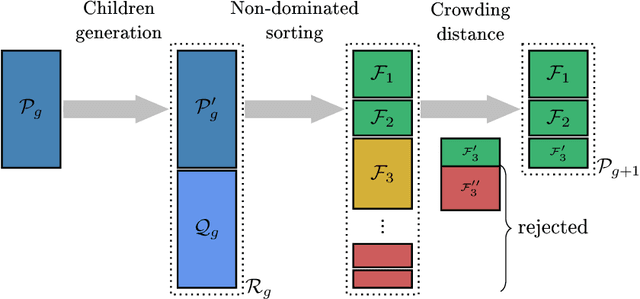
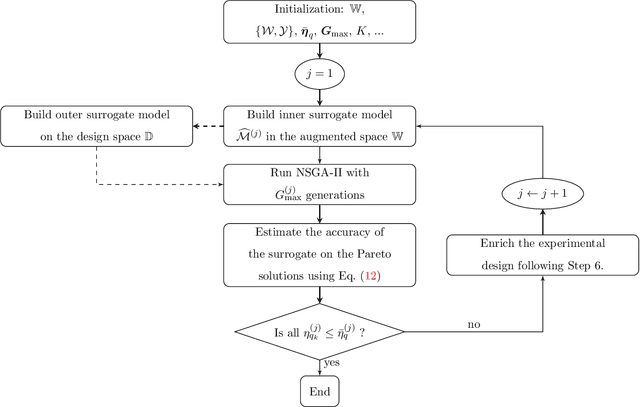
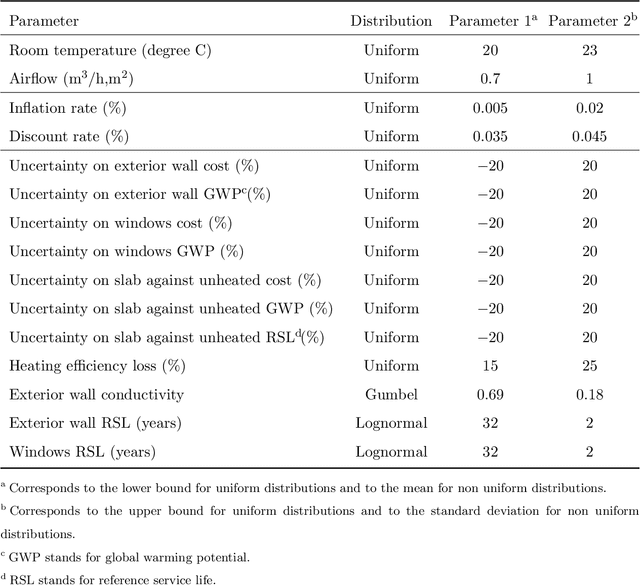
Explicitly accounting for uncertainties is paramount to the safety of engineering structures. Optimization which is often carried out at the early stage of the structural design offers an ideal framework for this task. When the uncertainties are mainly affecting the objective function, robust design optimization is traditionally considered. This work further assumes the existence of multiple and competing objective functions that need to be dealt with simultaneously. The optimization problem is formulated by considering quantiles of the objective functions which allows for the combination of both optimality and robustness in a single metric. By introducing the concept of common random numbers, the resulting nested optimization problem may be solved using a general-purpose solver, herein the non-dominated sorting genetic algorithm (NSGA-II). The computational cost of such an approach is however a serious hurdle to its application in real-world problems. We therefore propose a surrogate-assisted approach using Kriging as an inexpensive approximation of the associated computational model. The proposed approach consists of sequentially carrying out NSGA-II while using an adaptively built Kriging model to estimate of the quantiles. Finally, the methodology is adapted to account for mixed categorical-continuous parameters as the applications involve the selection of qualitative design parameters as well. The methodology is first applied to two analytical examples showing its efficiency. The third application relates to the selection of optimal renovation scenarios of a building considering both its life cycle cost and environmental impact. It shows that when it comes to renovation, the heating system replacement should be the priority.

A generalized framework for active learning reliability: survey and benchmark

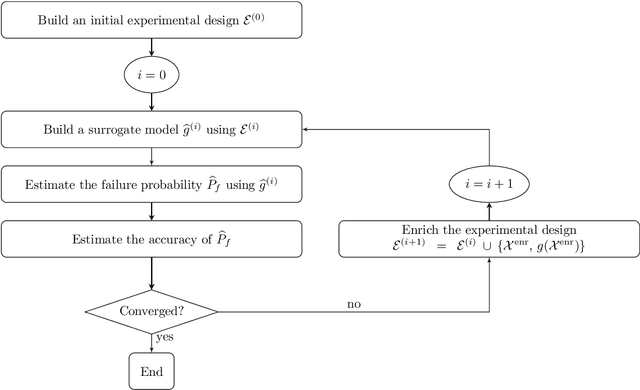
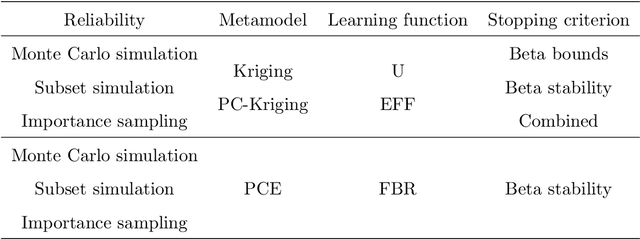
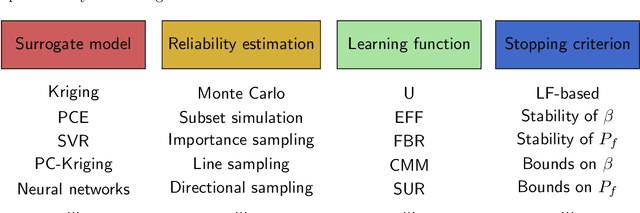
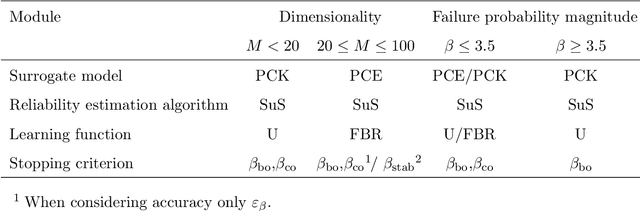
Active learning methods have recently surged in the literature due to their ability to solve complex structural reliability problems within an affordable computational cost. These methods are designed by adaptively building an inexpensive surrogate of the original limit-state function. Examples of such surrogates include Gaussian process models which have been adopted in many contributions, the most popular ones being the efficient global reliability analysis (EGRA) and the active Kriging Monte Carlo simulation (AK-MCS), two milestone contributions in the field. In this paper, we first conduct a survey of the recent literature, showing that most of the proposed methods actually span from modifying one or more aspects of the two aforementioned methods. We then propose a generalized modular framework to build on-the-fly efficient active learning strategies by combining the following four ingredients or modules: surrogate model, reliability estimation algorithm, learning function and stopping criterion. Using this framework, we devise 39 strategies for the solution of 20 reliability benchmark problems. The results of this extensive benchmark are analyzed under various criteria leading to a synthesized set of recommendations for practitioners. These may be refined with a priori knowledge about the feature of the problem to solve, i.e., dimensionality and magnitude of the failure probability. This benchmark has eventually highlighted the importance of using surrogates in conjunction with sophisticated reliability estimation algorithms as a way to enhance the efficiency of the latter.