mNARX+: A surrogate model for complex dynamical systems using manifold-NARX and automatic feature selection

We propose an automatic approach for manifold nonlinear autoregressive with exogenous inputs (mNARX) modeling that leverages the feature-based structure of functional-NARX (F-NARX) modeling. This novel approach, termed mNARX+, preserves the key strength of the mNARX framework, which is its expressivity allowing it to model complex dynamical systems, while simultaneously addressing a key limitation: the heavy reliance on domain expertise to identify relevant auxiliary quantities and their causal ordering. Our method employs a data-driven, recursive algorithm that automates the construction of the mNARX model sequence. It operates by sequentially selecting temporal features based on their correlation with the model prediction residuals, thereby automatically identifying the most critical auxiliary quantities and the order in which they should be modeled. This procedure significantly reduces the need for prior system knowledge. We demonstrate the effectiveness of the mNARX+ algorithm on two case studies: a Bouc-Wen oscillator with strong hysteresis and a complex aero-servo-elastic wind turbine simulator. The results show that the algorithm provides a systematic, data-driven method for creating accurate and stable surrogate models for complex dynamical systems.

Surrogate modeling for uncertainty quantification in nonlinear dynamics

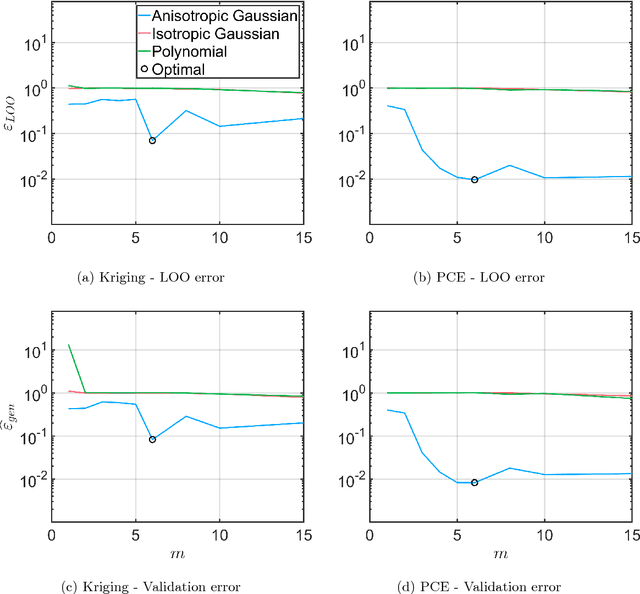
Predicting the behavior of complex systems in engineering often involves significant uncertainty about operating conditions, such as external loads, environmental effects, and manufacturing variability. As a result, uncertainty quantification (UQ) has become a critical tool in modeling-based engineering, providing methods to identify, characterize, and propagate uncertainty through computational models. However, the stochastic nature of UQ typically requires numerous evaluations of these models, which can be computationally expensive and limit the scope of feasible analyses. To address this, surrogate models, i.e., efficient functional approximations trained on a limited set of simulations, have become central in modern UQ practice. This book chapter presents a concise review of surrogate modeling techniques for UQ, with a focus on the particularly challenging task of capturing the full time-dependent response of dynamical systems. It introduces a classification of time-dependent problems based on the complexity of input excitation and discusses corresponding surrogate approaches, including combinations of principal component analysis with polynomial chaos expansions, time warping techniques, and nonlinear autoregressive models with exogenous inputs (NARX models). Each method is illustrated with simple application examples to clarify the underlying ideas and practical use.

Rare event estimation using stochastic spectral embedding

Estimating the probability of rare failure events is an essential step in the reliability assessment of engineering systems. Computing this failure probability for complex non-linear systems is challenging, and has recently spurred the development of active-learning reliability methods. These methods approximate the limit-state function (LSF) using surrogate models trained with a sequentially enriched set of model evaluations. A recently proposed method called stochastic spectral embedding (SSE) aims to improve the local approximation accuracy of global, spectral surrogate modelling techniques by sequentially embedding local residual expansions in subdomains of the input space. In this work we apply SSE to the LSF, giving rise to a stochastic spectral embedding-based reliability (SSER) method. The resulting partition of the input space decomposes the failure probability into a set of easy-to-compute domain-wise failure probabilities. We propose a set of modifications that tailor the algorithm to efficiently solve rare event estimation problems. These modifications include specialized refinement domain selection, partitioning and enrichment strategies. We showcase the algorithm performance on four benchmark problems of various dimensionality and complexity in the LSF.

A generalized framework for active learning reliability: survey and benchmark

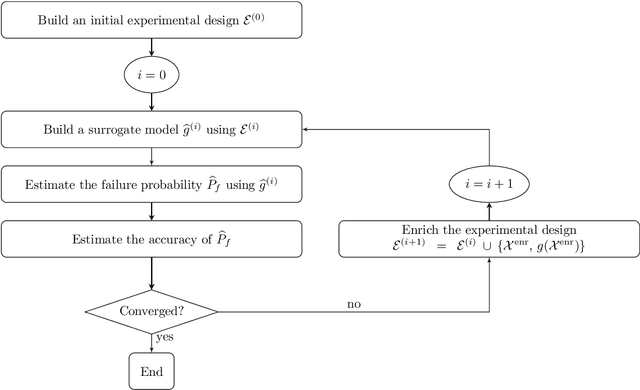
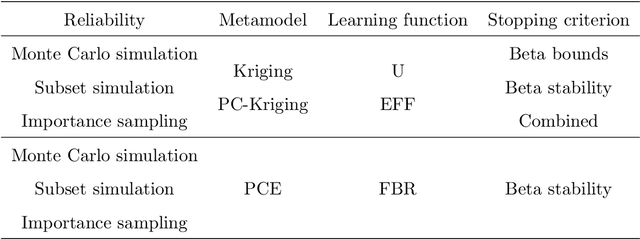
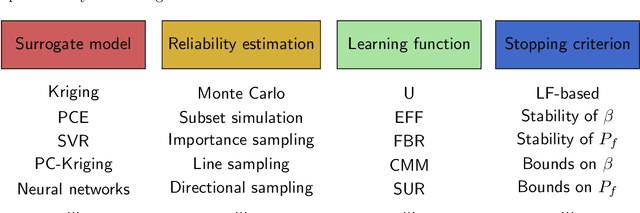
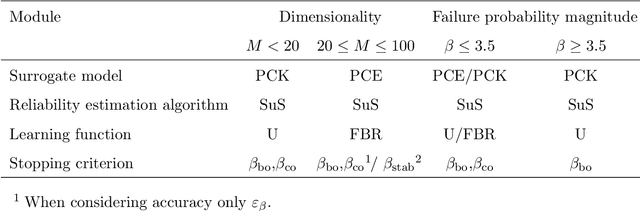
Active learning methods have recently surged in the literature due to their ability to solve complex structural reliability problems within an affordable computational cost. These methods are designed by adaptively building an inexpensive surrogate of the original limit-state function. Examples of such surrogates include Gaussian process models which have been adopted in many contributions, the most popular ones being the efficient global reliability analysis (EGRA) and the active Kriging Monte Carlo simulation (AK-MCS), two milestone contributions in the field. In this paper, we first conduct a survey of the recent literature, showing that most of the proposed methods actually span from modifying one or more aspects of the two aforementioned methods. We then propose a generalized modular framework to build on-the-fly efficient active learning strategies by combining the following four ingredients or modules: surrogate model, reliability estimation algorithm, learning function and stopping criterion. Using this framework, we devise 39 strategies for the solution of 20 reliability benchmark problems. The results of this extensive benchmark are analyzed under various criteria leading to a synthesized set of recommendations for practitioners. These may be refined with a priori knowledge about the feature of the problem to solve, i.e., dimensionality and magnitude of the failure probability. This benchmark has eventually highlighted the importance of using surrogates in conjunction with sophisticated reliability estimation algorithms as a way to enhance the efficiency of the latter.

Stochastic spectral embedding

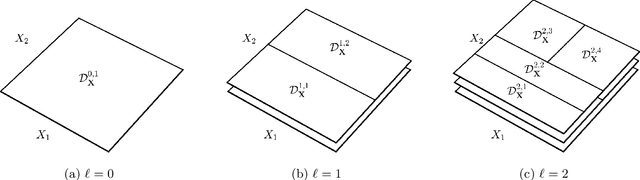
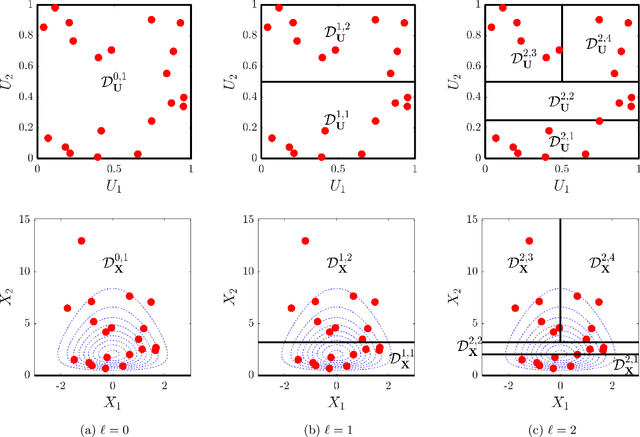
Constructing approximations that can accurately mimic the behaviour of complex models at reduced computational costs is an important aspect of uncertainty quantification. Despite their flexibility and efficiency, classical surrogate models such as Kriging or polynomial chaos expansions tend to struggle with highly non-linear, localized or non-stationary computational models. We hereby propose a novel sequential adaptive surrogate modelling method based on recursively embedding locally spectral expansions. It is achieved by means of disjoint recursive partitioning of the input domain, which consists in sequentially splitting the latter into smaller subdomains, and constructing a simpler local spectral expansions in each, exploiting the trade-off complexity vs. locality. The resulting expansion, which we refer to as "stochastic spectral embedding" (SSE), is a piece-wise continuous approximation of the model response that shows promising approximation capabilities, and good scaling with both the problem dimension and the size of the training set. We finally show how the method compares favourably against state-of-the-art sparse polynomial chaos expansions on a set of models with different complexity and input dimension.

Extending classical surrogate modelling to ultrahigh dimensional problems through supervised dimensionality reduction: a data-driven approach

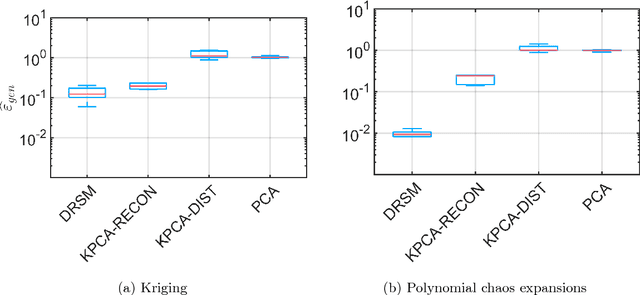
Thanks to their versatility, ease of deployment and high-performance, surrogate models have become staple tools in the arsenal of uncertainty quantification (UQ). From local interpolants to global spectral decompositions, surrogates are characterised by their ability to efficiently emulate complex computational models based on a small set of model runs used for training. An inherent limitation of many surrogate models is their susceptibility to the curse of dimensionality, which traditionally limits their applicability to a maximum of $\co(10^2)$ input dimensions. We present a novel approach at high-dimensional surrogate modelling that is model-, dimensionality reduction- and surrogate model- agnostic (black box), and can enable the solution of high dimensional (i.e. up to $\co(10^4)$) problems. After introducing the general algorithm, we demonstrate its performance by combining Kriging and polynomial chaos expansions surrogates and kernel principal component analysis. In particular, we compare the generalisation performance that the resulting surrogates achieve to the classical sequential application of dimensionality reduction followed by surrogate modelling on several benchmark applications, comprising an analytical function and two engineering applications of increasing dimensionality and complexity.

Data-driven polynomial chaos expansion for machine learning regression

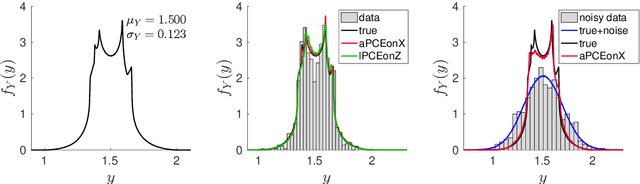
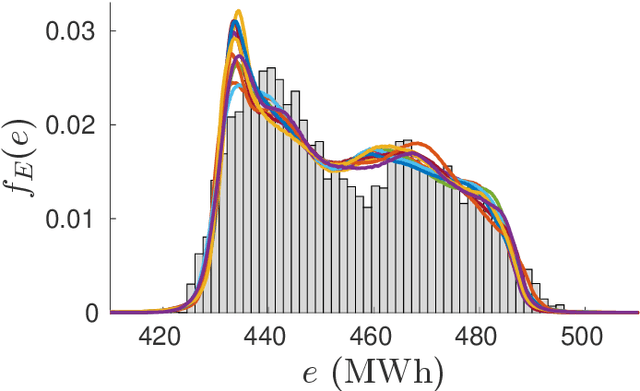
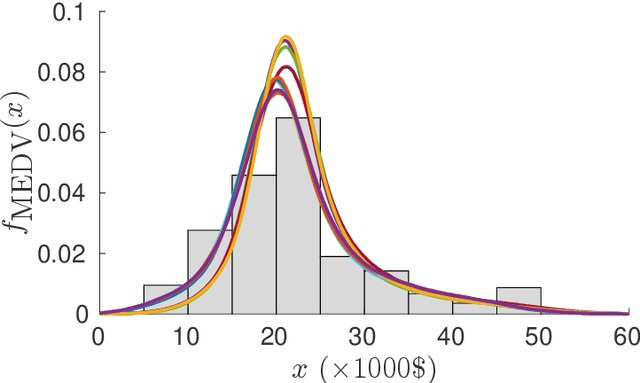
We present a regression technique for data driven problems based on polynomial chaos expansion (PCE). PCE is a popular technique in the field of uncertainty quantification (UQ), where it is typically used to replace a runnable but expensive computational model subject to random inputs with an inexpensive-to-evaluate polynomial function. The metamodel obtained enables a reliable estimation of the statistics of the output, provided that a suitable probabilistic model of the input is available. In classical machine learning (ML) regression settings, however, the system is only known through observations of its inputs and output, and the interest lies in obtaining accurate pointwise predictions of the latter. Here, we show that a PCE metamodel purely trained on data can yield pointwise predictions whose accuracy is comparable to that of other ML regression models, such as neural networks and support vector machines. The comparisons are performed on benchmark datasets available from the literature. The methodology also enables the quantification of the output uncertainties and is robust to noise. Furthermore, it enjoys additional desirable properties, such as good performance for small training sets and simplicity of construction, with only little parameter tuning required. In the presence of statistically dependent inputs, we investigate two ways to build the PCE, and show through simulations that one approach is superior to the other in the stated settings.