Rare event estimation using stochastic spectral embedding

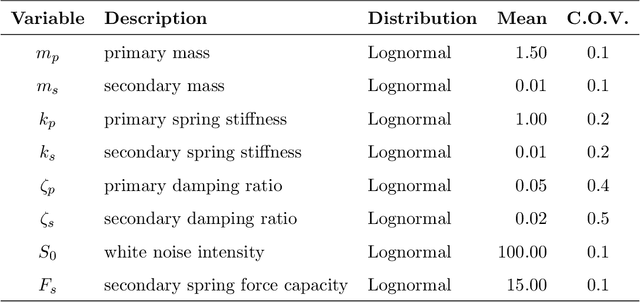
Estimating the probability of rare failure events is an essential step in the reliability assessment of engineering systems. Computing this failure probability for complex non-linear systems is challenging, and has recently spurred the development of active-learning reliability methods. These methods approximate the limit-state function (LSF) using surrogate models trained with a sequentially enriched set of model evaluations. A recently proposed method called stochastic spectral embedding (SSE) aims to improve the local approximation accuracy of global, spectral surrogate modelling techniques by sequentially embedding local residual expansions in subdomains of the input space. In this work we apply SSE to the LSF, giving rise to a stochastic spectral embedding-based reliability (SSER) method. The resulting partition of the input space decomposes the failure probability into a set of easy-to-compute domain-wise failure probabilities. We propose a set of modifications that tailor the algorithm to efficiently solve rare event estimation problems. These modifications include specialized refinement domain selection, partitioning and enrichment strategies. We showcase the algorithm performance on four benchmark problems of various dimensionality and complexity in the LSF.

Stochastic spectral embedding

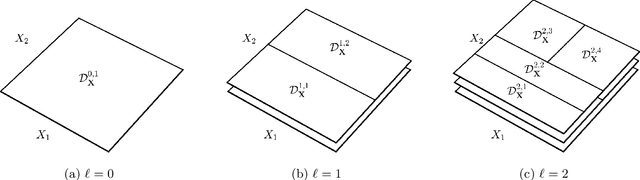
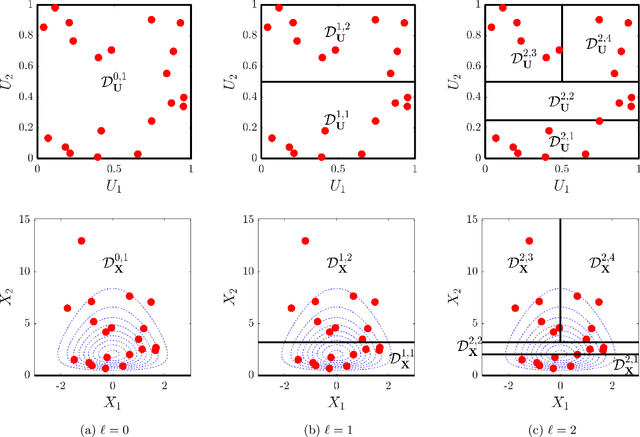
Constructing approximations that can accurately mimic the behaviour of complex models at reduced computational costs is an important aspect of uncertainty quantification. Despite their flexibility and efficiency, classical surrogate models such as Kriging or polynomial chaos expansions tend to struggle with highly non-linear, localized or non-stationary computational models. We hereby propose a novel sequential adaptive surrogate modelling method based on recursively embedding locally spectral expansions. It is achieved by means of disjoint recursive partitioning of the input domain, which consists in sequentially splitting the latter into smaller subdomains, and constructing a simpler local spectral expansions in each, exploiting the trade-off complexity vs. locality. The resulting expansion, which we refer to as "stochastic spectral embedding" (SSE), is a piece-wise continuous approximation of the model response that shows promising approximation capabilities, and good scaling with both the problem dimension and the size of the training set. We finally show how the method compares favourably against state-of-the-art sparse polynomial chaos expansions on a set of models with different complexity and input dimension.