Lower bounds for learning quantum states with single-copy measurements

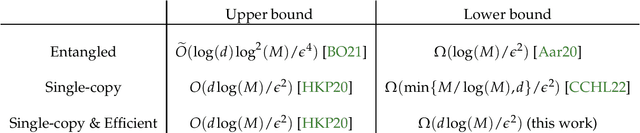
We study the problems of quantum tomography and shadow tomography using measurements performed on individual, identical copies of an unknown $d$-dimensional state. We first revisit a known lower bound due to Haah et al. (2017) on quantum tomography with accuracy $\epsilon$ in trace distance, when the measurements choices are independent of previously observed outcomes (i.e., they are nonadaptive). We give a succinct proof of this result. This leads to stronger lower bounds when the learner uses measurements with a constant number of outcomes. In particular, this rigorously establishes the optimality of the folklore ``Pauli tomography" algorithm in terms of its sample complexity. We also derive novel bounds of $\Omega(r^2 d/\epsilon^2)$ and $\Omega(r^2 d^2/\epsilon^2)$ for learning rank $r$ states using arbitrary and constant-outcome measurements, respectively, in the nonadaptive case. In addition to the sample complexity, a resource of practical significance for learning quantum states is the number of different measurements used by an algorithm. We extend our lower bounds to the case where the learner performs possibly adaptive measurements from a fixed set of $\exp(O(d))$ measurements. This implies in particular that adaptivity does not give us any advantage using single-copy measurements that are efficiently implementable. We also obtain a similar bound in the case where the goal is to predict the expectation values of a given sequence of observables, a task known as shadow tomography. Finally, in the case of adaptive, single-copy measurements implementable with polynomial-size circuits, we prove that a straightforward strategy based on computing sample means of the given observables is optimal.

Adaptive shot allocation for fast convergence in variational quantum algorithms

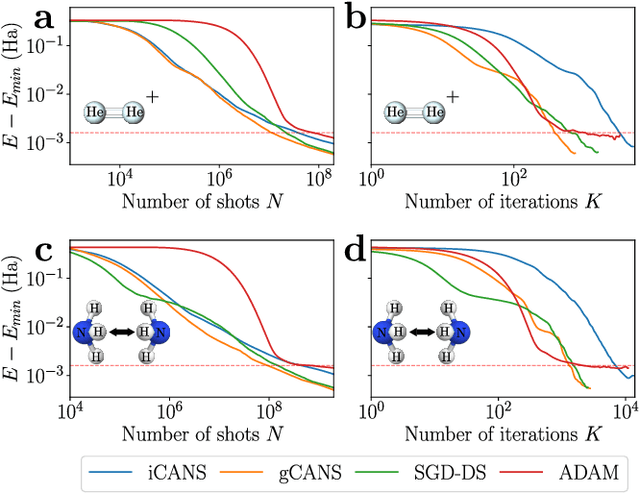
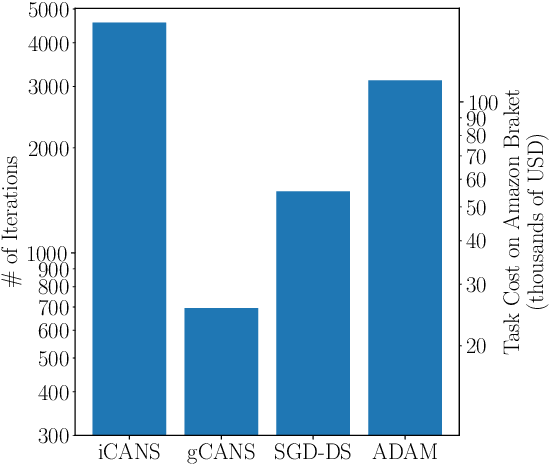
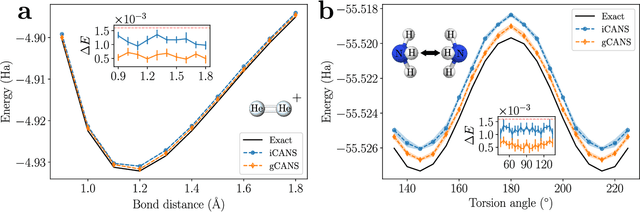
Variational Quantum Algorithms (VQAs) are a promising approach for practical applications like chemistry and materials science on near-term quantum computers as they typically reduce quantum resource requirements. However, in order to implement VQAs, an efficient classical optimization strategy is required. Here we present a new stochastic gradient descent method using an adaptive number of shots at each step, called the global Coupled Adaptive Number of Shots (gCANS) method, which improves on prior art in both the number of iterations as well as the number of shots required. These improvements reduce both the time and money required to run VQAs on current cloud platforms. We analytically prove that in a convex setting gCANS achieves geometric convergence to the optimum. Further, we numerically investigate the performance of gCANS on some chemical configuration problems. We also consider finding the ground state for an Ising model with different numbers of spins to examine the scaling of the method. We find that for these problems, gCANS compares favorably to all of the other optimizers we consider.