ConstrainedZero: Chance-Constrained POMDP Planning using Learned Probabilistic Failure Surrogates and Adaptive Safety Constraints

To plan safely in uncertain environments, agents must balance utility with safety constraints. Safe planning problems can be modeled as a chance-constrained partially observable Markov decision process (CC-POMDP) and solutions often use expensive rollouts or heuristics to estimate the optimal value and action-selection policy. This work introduces the ConstrainedZero policy iteration algorithm that solves CC-POMDPs in belief space by learning neural network approximations of the optimal value and policy with an additional network head that estimates the failure probability given a belief. This failure probability guides safe action selection during online Monte Carlo tree search (MCTS). To avoid overemphasizing search based on the failure estimates, we introduce $\Delta$-MCTS, which uses adaptive conformal inference to update the failure threshold during planning. The approach is tested on a safety-critical POMDP benchmark, an aircraft collision avoidance system, and the sustainability problem of safe CO$_2$ storage. Results show that by separating safety constraints from the objective we can achieve a target level of safety without optimizing the balance between rewards and costs.

Addressing Myopic Constrained POMDP Planning with Recursive Dual Ascent

Lagrangian-guided Monte Carlo tree search with global dual ascent has been applied to solve large constrained partially observable Markov decision processes (CPOMDPs) online. In this work, we demonstrate that these global dual parameters can lead to myopic action selection during exploration, ultimately leading to suboptimal decision making. To address this, we introduce history-dependent dual variables that guide local action selection and are optimized with recursive dual ascent. We empirically compare the performance of our approach on a motivating toy example and two large CPOMDPs, demonstrating improved exploration, and ultimately, safer outcomes.

Constrained Hierarchical Monte Carlo Belief-State Planning

Optimal plans in Constrained Partially Observable Markov Decision Processes (CPOMDPs) maximize reward objectives while satisfying hard cost constraints, generalizing safe planning under state and transition uncertainty. Unfortunately, online CPOMDP planning is extremely difficult in large or continuous problem domains. In many large robotic domains, hierarchical decomposition can simplify planning by using tools for low-level control given high-level action primitives (options). We introduce Constrained Options Belief Tree Search (COBeTS) to leverage this hierarchy and scale online search-based CPOMDP planning to large robotic problems. We show that if primitive option controllers are defined to satisfy assigned constraint budgets, then COBeTS will satisfy constraints anytime. Otherwise, COBeTS will guide the search towards a safe sequence of option primitives, and hierarchical monitoring can be used to achieve runtime safety. We demonstrate COBeTS in several safety-critical, constrained partially observable robotic domains, showing that it can plan successfully in continuous CPOMDPs while non-hierarchical baselines cannot.

Online Planning for Constrained POMDPs with Continuous Spaces through Dual Ascent

Rather than augmenting rewards with penalties for undesired behavior, Constrained Partially Observable Markov Decision Processes (CPOMDPs) plan safely by imposing inviolable hard constraint value budgets. Previous work performing online planning for CPOMDPs has only been applied to discrete action and observation spaces. In this work, we propose algorithms for online CPOMDP planning for continuous state, action, and observation spaces by combining dual ascent with progressive widening. We empirically compare the effectiveness of our proposed algorithms on continuous CPOMDPs that model both toy and real-world safety-critical problems. Additionally, we compare against the use of online solvers for continuous unconstrained POMDPs that scalarize cost constraints into rewards, and investigate the effect of optimistic cost propagation.

Meta-SysId: A Meta-Learning Approach for Simultaneous Identification and Prediction

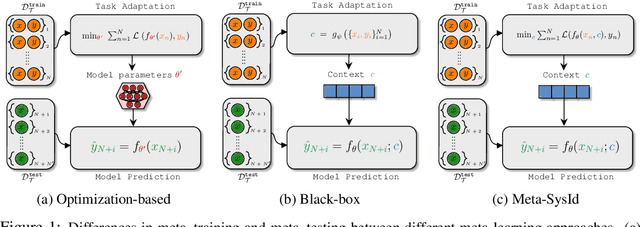
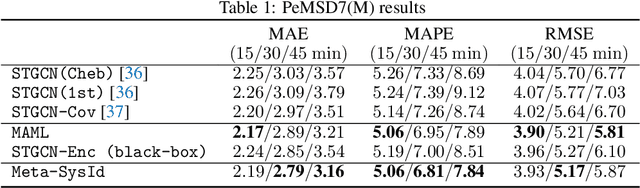
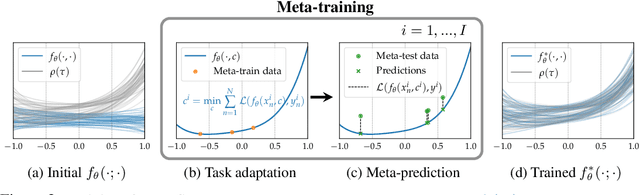
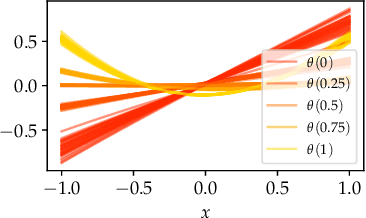
In this paper, we propose Meta-SysId, a meta-learning approach to model sets of systems that have behavior governed by common but unknown laws and that differentiate themselves by their context. Inspired by classical modeling-and-identification approaches, Meta-SysId learns to represent the common law through shared parameters and relies on online optimization to compute system-specific context. Compared to optimization-based meta-learning methods, the separation between class parameters and context variables reduces the computational burden while allowing batch computations and a simple training scheme. We test Meta-SysId on polynomial regression, time-series prediction, model-based control, and real-world traffic prediction domains, empirically finding it outperforms or is competitive with meta-learning baselines.

SHAIL: Safety-Aware Hierarchical Adversarial Imitation Learning for Autonomous Driving in Urban Environments

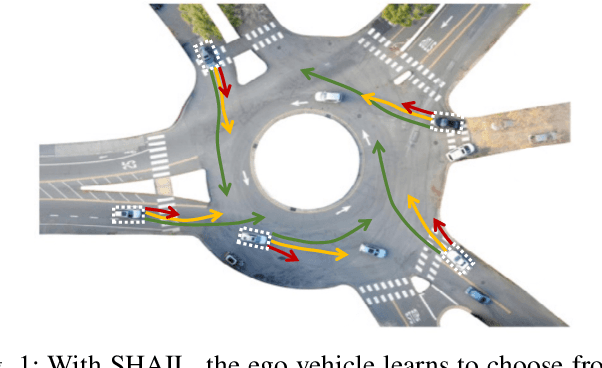
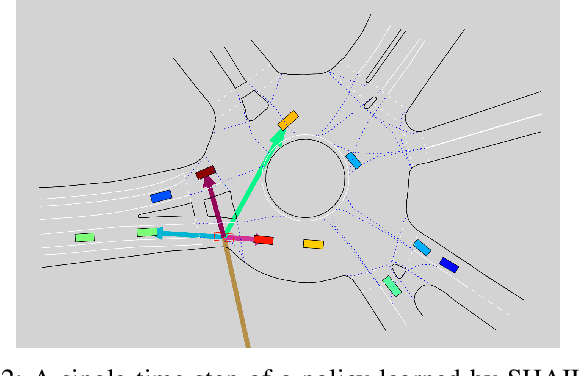
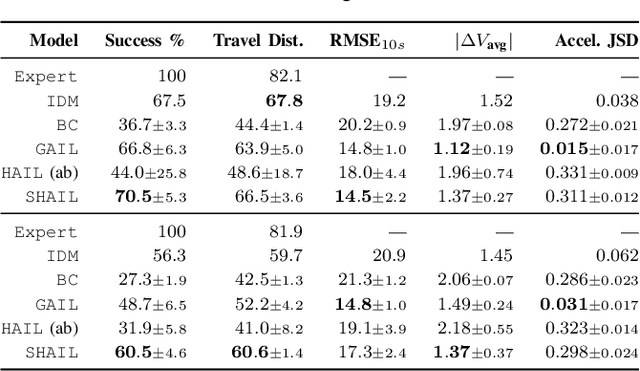
Designing a safe and human-like decision-making system for an autonomous vehicle is a challenging task. Generative imitation learning is one possible approach for automating policy-building by leveraging both real-world and simulated decisions. Previous work that applies generative imitation learning to autonomous driving policies focuses on learning a low-level controller for simple settings. However, to scale to complex settings, many autonomous driving systems combine fixed, safe, optimization-based low-level controllers with high-level decision-making logic that selects the appropriate task and associated controller. In this paper, we attempt to bridge this gap in complexity by employing Safety-Aware Hierarchical Adversarial Imitation Learning (SHAIL), a method for learning a high-level policy that selects from a set of low-level controller instances in a way that imitates low-level driving data on-policy. We introduce an urban roundabout simulator that controls non-ego vehicles using real data from the Interaction dataset. We then show empirically that our approach can produce better behavior than previous approaches in driver imitation which have difficulty scaling to complex environments. Our implementation is available at https://github.com/sisl/InteractionImitation.

Conditional Approximate Normalizing Flows for Joint Multi-Step Probabilistic Forecasting with Application to Electricity Demand

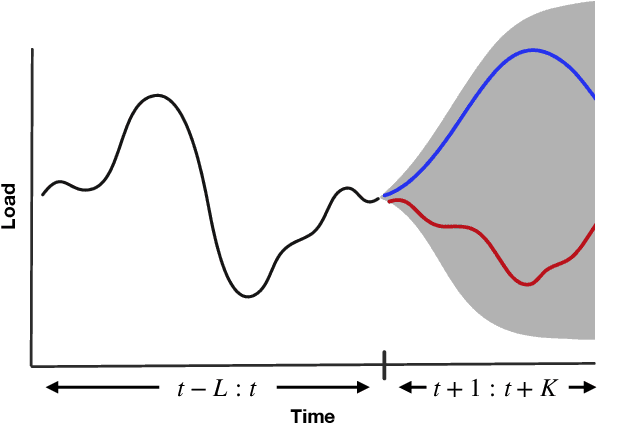
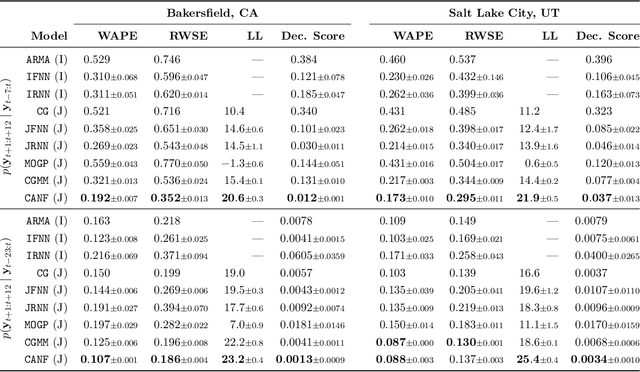
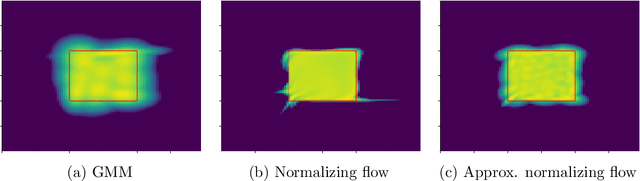
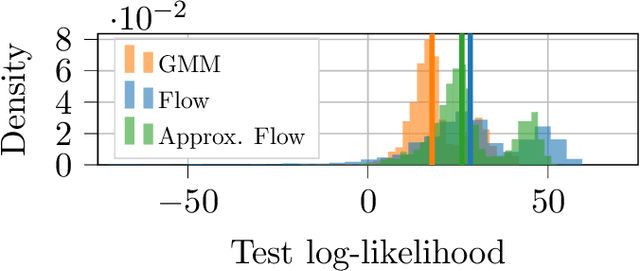
Some real-world decision-making problems require making probabilistic forecasts over multiple steps at once. However, methods for probabilistic forecasting may fail to capture correlations in the underlying time-series that exist over long time horizons as errors accumulate. One such application is with resource scheduling under uncertainty in a grid environment, which requires forecasting electricity demand that is inherently noisy, but often cyclic. In this paper, we introduce the conditional approximate normalizing flow (CANF) to make probabilistic multi-step time-series forecasts when correlations are present over long time horizons. We first demonstrate our method's efficacy on estimating the density of a toy distribution, finding that CANF improves the KL divergence by one-third compared to that of a Gaussian mixture model while still being amenable to explicit conditioning. We then use a publicly available household electricity consumption dataset to showcase the effectiveness of CANF on joint probabilistic multi-step forecasting. Empirical results show that conditional approximate normalizing flows outperform other methods in terms of multi-step forecast accuracy and lead to up to 10x better scheduling decisions. Our implementation is available at https://github.com/sisl/JointDemandForecasting.

Multi-Vehicle Control in Roundabouts using Decentralized Game-Theoretic Planning

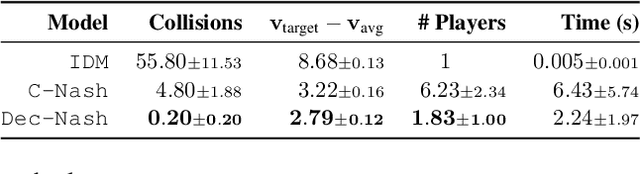
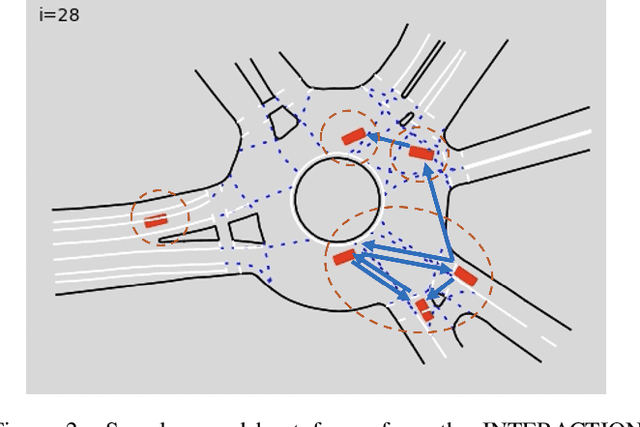
Safe navigation in dense, urban driving environments remains an open problem and an active area of research. Unlike typical predict-then-plan approaches, game-theoretic planning considers how one vehicle's plan will affect the actions of another. Recent work has demonstrated significant improvements in the time required to find local Nash equilibria in general-sum games with nonlinear objectives and constraints. When applied trivially to driving, these works assume all vehicles in a scene play a game together, which can result in intractable computation times for dense traffic. We formulate a decentralized approach to game-theoretic planning by assuming that agents only play games within their observational vicinity, which we believe to be a more reasonable assumption for human driving. Games are played in parallel for all strongly connected components of an interaction graph, significantly reducing the number of players and constraints in each game, and therefore the time required for planning. We demonstrate that our approach can achieve collision-free, efficient driving in urban environments by comparing performance against an adaptation of the Intelligent Driver Model and centralized game-theoretic planning when navigating roundabouts in the INTERACTION dataset. Our implementation is available at http://github.com/sisl/DecNashPlanning.