World Model Failure Classification and Anomaly Detection for Autonomous Inspection

Autonomous inspection robots for monitoring industrial sites can reduce costs and risks associated with human-led inspection. However, accurate readings can be challenging due to occlusions, limited viewpoints, or unexpected environmental conditions. We propose a hybrid framework that combines supervised failure classification with anomaly detection, enabling classification of inspection tasks as a success, known failure, or anomaly (i.e., out-of-distribution) case. Our approach uses a world model backbone with compressed video inputs. This policy-agnostic, distribution-free framework determines classifications based on two decision functions set by conformal prediction (CP) thresholds before a human observer does. We evaluate the framework on gauge inspection feeds collected from office and industrial sites and demonstrate real-time deployment on a Boston Dynamics Spot. Experiments show over 90% accuracy in distinguishing between successes, failures, and OOD cases, with classifications occurring earlier than a human observer. These results highlight the potential for robust, anticipatory failure detection in autonomous inspection tasks or as a feedback signal for model training to assess and improve the quality of training data. Project website: https://autoinspection-classification.github.io

Model Identification Adaptive Control with $ρ$-POMDP Planning

Accurate system modeling is crucial for safe, effective control, as misidentification can lead to accumulated errors, especially under partial observability. We address this problem by formulating informative input design (IID) and model identification adaptive control (MIAC) as belief space planning problems, modeled as partially observable Markov decision processes with belief-dependent rewards ($\rho$-POMDPs). We treat system parameters as hidden state variables that must be localized while simultaneously controlling the system. We solve this problem with an adapted belief-space iterative Linear Quadratic Regulator (BiLQR). We demonstrate it on fully and partially observable tasks for cart-pole and steady aircraft flight domains. Our method outperforms baselines such as regression, filtering, and local optimal control methods, even under instantaneous disturbances to system parameters.

Comparing the Complexity of Robotic Tasks

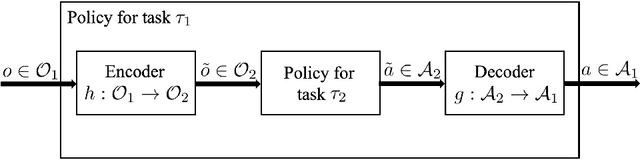
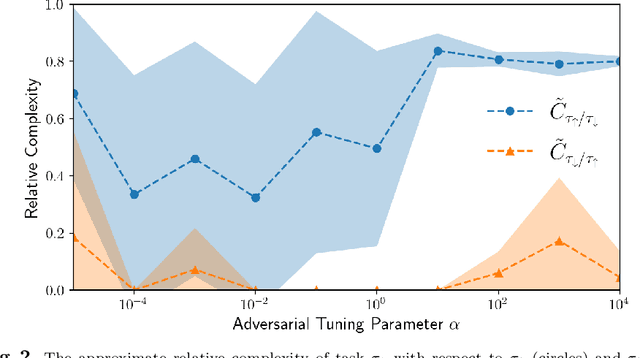
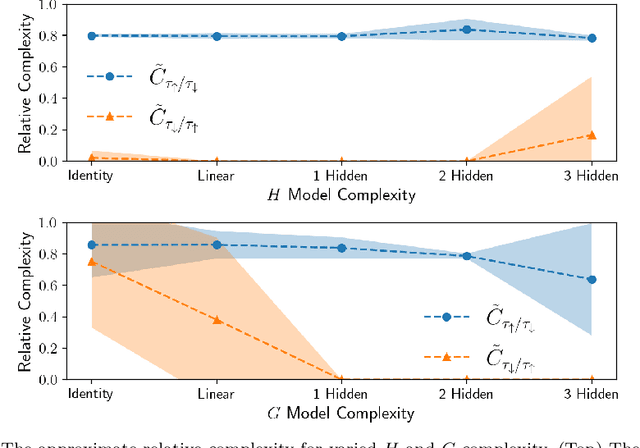
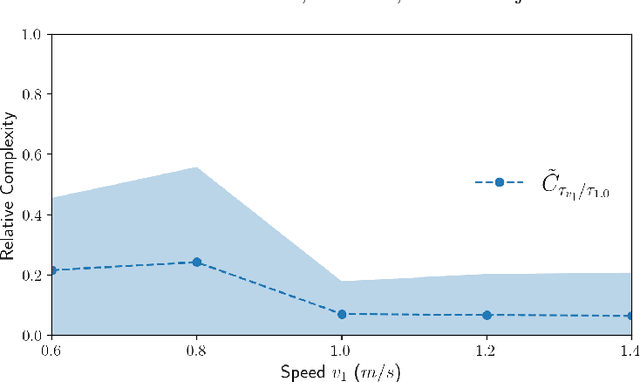
We are motivated by the problem of comparing the complexity of one robotic task relative to another. To this end, we define a notion of reduction that formalizes the following intuition: Task 1 reduces to Task 2 if we can efficiently transform any policy that solves Task 2 into a policy that solves Task 1. We further define a quantitative measure of the relative complexity between any two tasks for a given robot. We prove useful properties of our notion of reduction (e.g., reflexivity, transitivity, and antisymmetry) and relative complexity measure (e.g., nonnegativity and monotonicity). In addition, we propose practical algorithms for estimating the relative complexity measure. We illustrate our framework for comparing robotic tasks using (i) examples where one can analytically establish reductions, and (ii) reinforcement learning examples where the proposed algorithm can estimate the relative complexity between tasks.