Provable Length Generalization in Sequence Prediction via Spectral Filtering

We consider the problem of length generalization in sequence prediction. We define a new metric of performance in this setting -- the Asymmetric-Regret -- which measures regret against a benchmark predictor with longer context length than available to the learner. We continue by studying this concept through the lens of the spectral filtering algorithm. We present a gradient-based learning algorithm that provably achieves length generalization for linear dynamical systems. We conclude with proof-of-concept experiments which are consistent with our theory.

Efficient Convex Optimization Requires Superlinear Memory

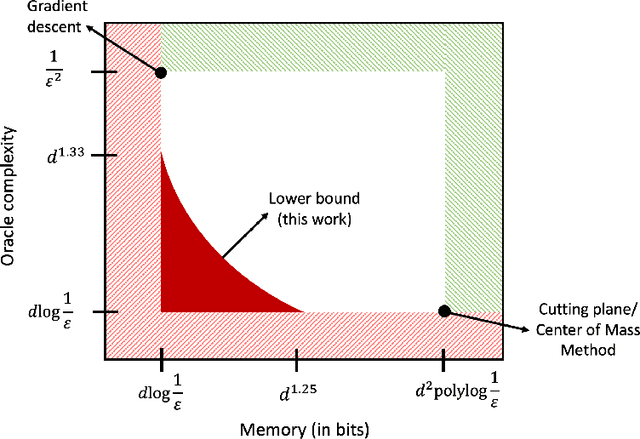
We show that any memory-constrained, first-order algorithm which minimizes $d$-dimensional, $1$-Lipschitz convex functions over the unit ball to $1/\mathrm{poly}(d)$ accuracy using at most $d^{1.25 - \delta}$ bits of memory must make at least $\tilde{\Omega}(d^{1 + (4/3)\delta})$ first-order queries (for any constant $\delta \in [0, 1/4]$). Consequently, the performance of such memory-constrained algorithms are a polynomial factor worse than the optimal $\tilde{O}(d)$ query bound for this problem obtained by cutting plane methods that use $\tilde{O}(d^2)$ memory. This resolves a COLT 2019 open problem of Woodworth and Srebro.

Big-Step-Little-Step: Efficient Gradient Methods for Objectives with Multiple Scales

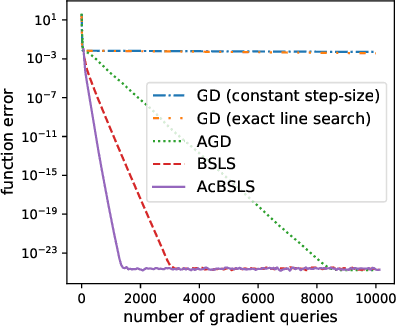
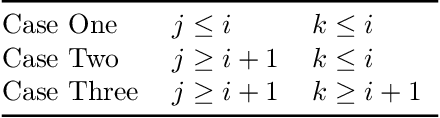
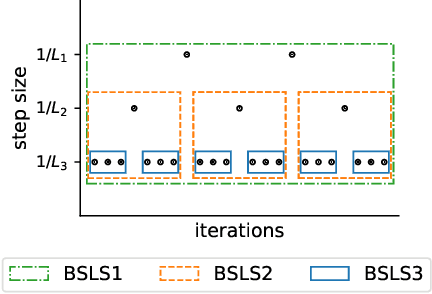
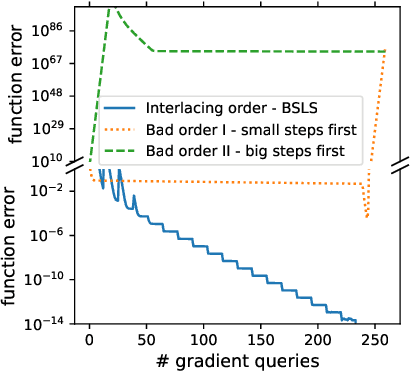
We provide new gradient-based methods for efficiently solving a broad class of ill-conditioned optimization problems. We consider the problem of minimizing a function $f : \mathbb{R}^d \rightarrow \mathbb{R}$ which is implicitly decomposable as the sum of $m$ unknown non-interacting smooth, strongly convex functions and provide a method which solves this problem with a number of gradient evaluations that scales (up to logarithmic factors) as the product of the square-root of the condition numbers of the components. This complexity bound (which we prove is nearly optimal) can improve almost exponentially on that of accelerated gradient methods, which grow as the square root of the condition number of $f$. Additionally, we provide efficient methods for solving stochastic, quadratic variants of this multiscale optimization problem. Rather than learn the decomposition of $f$ (which would be prohibitively expensive), our methods apply a clean recursive "Big-Step-Little-Step" interleaving of standard methods. The resulting algorithms use $\tilde{\mathcal{O}}(d m)$ space, are numerically stable, and open the door to a more fine-grained understanding of the complexity of convex optimization beyond condition number.

On Misspecification in Prediction Problems and Robustness via Improper Learning

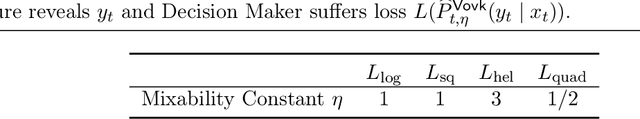
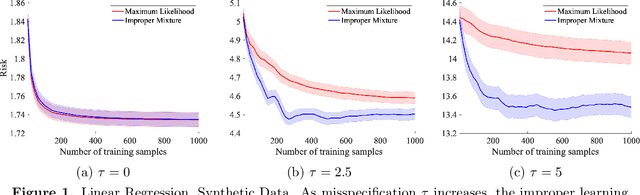
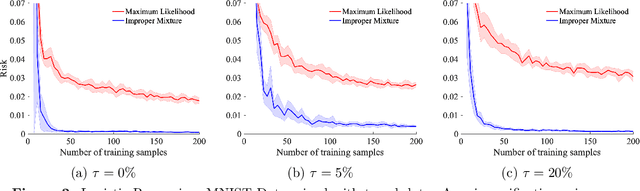
We study probabilistic prediction games when the underlying model is misspecified, investigating the consequences of predicting using an incorrect parametric model. We show that for a broad class of loss functions and parametric families of distributions, the regret of playing a "proper" predictor -- one from the putative model class -- relative to the best predictor in the same model class has lower bound scaling at least as $\sqrt{\gamma n}$, where $\gamma$ is a measure of the model misspecification to the true distribution in terms of total variation distance. In contrast, using an aggregation-based (improper) learner, one can obtain regret $d \log n$ for any underlying generating distribution, where $d$ is the dimension of the parameter; we exhibit instances in which this is unimprovable even over the family of all learners that may play distributions in the convex hull of the parametric family. These results suggest that simple strategies for aggregating multiple learners together should be more robust, and several experiments conform to this hypothesis.

Sequential Matrix Completion

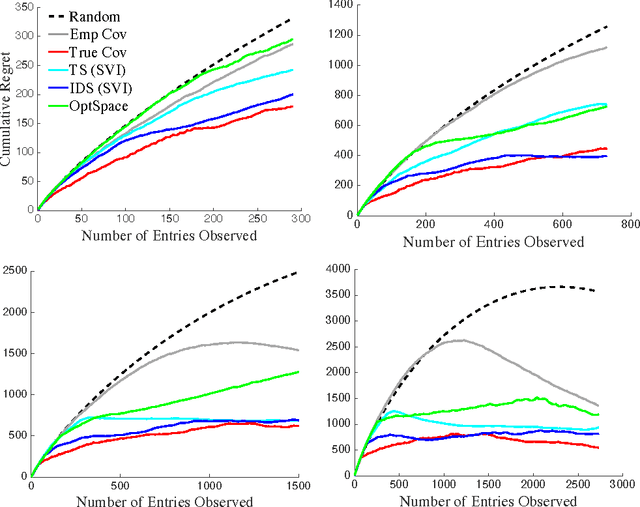
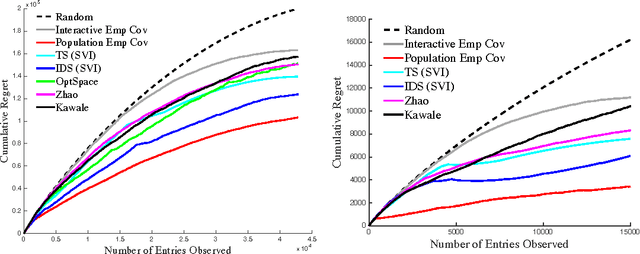
We propose a novel algorithm for sequential matrix completion in a recommender system setting, where the $(i,j)$th entry of the matrix corresponds to a user $i$'s rating of product $j$. The objective of the algorithm is to provide a sequential policy for user-product pair recommendation which will yield the highest possible ratings after a finite time horizon. The algorithm uses a Gamma process factor model with two posterior-focused bandit policies, Thompson Sampling and Information-Directed Sampling. While Thompson Sampling shows competitive performance in simulations, state-of-the-art performance is obtained from Information-Directed Sampling, which makes its recommendations based off a ratio between the expected reward and a measure of information gain. To our knowledge, this is the first implementation of Information Directed Sampling on large real datasets. This approach contributes to a recent line of research on bandit approaches to collaborative filtering including Kawale et al. (2015), Li et al. (2010), Bresler et al. (2014), Li et al. (2016), Deshpande & Montanari (2012), and Zhao et al. (2013). The setting of this paper, as has been noted in Kawale et al. (2015) and Zhao et al. (2013), presents significant challenges to bounding regret after finite horizons. We discuss these challenges in relation to simpler models for bandits with side information, such as linear or gaussian process bandits, and hope the experiments presented here motivate further research toward theoretical guarantees.