Efficiently Learning Mixtures of Mallows Models

Mixtures of Mallows models are a popular generative model for ranking data coming from a heterogeneous population. They have a variety of applications including social choice, recommendation systems and natural language processing. Here we give the first polynomial time algorithm for provably learning the parameters of a mixture of Mallows models with any constant number of components. Prior to our work, only the two component case had been settled. Our analysis revolves around a determinantal identity of Zagier which was proven in the context of mathematical physics, which we use to show polynomial identifiability and ultimately to construct test functions to peel off one component at a time. To complement our upper bounds, we show information-theoretic lower bounds on the sample complexity as well as lower bounds against restricted families of algorithms that make only local queries. Together, these results demonstrate various impediments to improving the dependence on the number of components. They also motivate the study of learning mixtures of Mallows models from the perspective of beyond worst-case analysis. In this direction, we show that when the scaling parameters of the Mallows models have separation, there are much faster learning algorithms.

Optimality and Sub-optimality of PCA I: Spiked Random Matrix Models

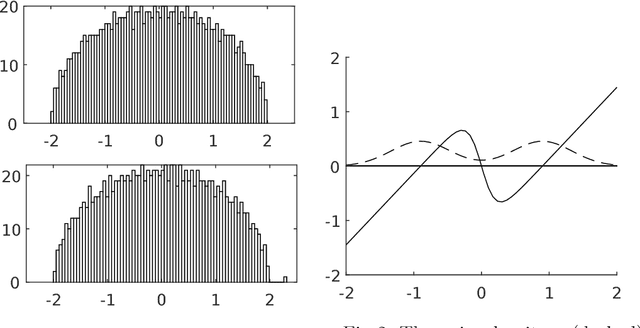
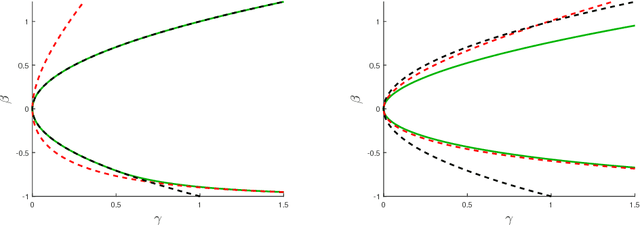
A central problem of random matrix theory is to understand the eigenvalues of spiked random matrix models, introduced by Johnstone, in which a prominent eigenvector (or "spike") is planted into a random matrix. These distributions form natural statistical models for principal component analysis (PCA) problems throughout the sciences. Baik, Ben Arous and Peche showed that the spiked Wishart ensemble exhibits a sharp phase transition asymptotically: when the spike strength is above a critical threshold, it is possible to detect the presence of a spike based on the top eigenvalue, and below the threshold the top eigenvalue provides no information. Such results form the basis of our understanding of when PCA can detect a low-rank signal in the presence of noise. However, under structural assumptions on the spike, not all information is necessarily contained in the spectrum. We study the statistical limits of tests for the presence of a spike, including non-spectral tests. Our results leverage Le Cam's notion of contiguity, and include: i) For the Gaussian Wigner ensemble, we show that PCA achieves the optimal detection threshold for certain natural priors for the spike. ii) For any non-Gaussian Wigner ensemble, PCA is sub-optimal for detection. However, an efficient variant of PCA achieves the optimal threshold (for natural priors) by pre-transforming the matrix entries. iii) For the Gaussian Wishart ensemble, the PCA threshold is optimal for positive spikes (for natural priors) but this is not always the case for negative spikes.

Learning Mixtures of Product Distributions via Higher Multilinear Moments

Learning mixtures of $k$ binary product distributions is a central problem in computational learning theory, but one where there are wide gaps between the best known algorithms and lower bounds (even for restricted families of algorithms). We narrow many of these gaps by developing novel insights about how to reason about higher order multilinear moments. Our results include: 1) An $n^{O(k^2)}$ time algorithm for learning mixtures of binary product distributions, giving the first improvement on the $n^{O(k^3)}$ time algorithm of Feldman, O'Donnell and Servedio 2) An $n^{\Omega(\sqrt{k})}$ statistical query lower bound, improving on the $n^{\Omega(\log k)}$ lower bound that is based on connections to sparse parity with noise 3) An $n^{O(\log k)}$ time algorithm for learning mixtures of $k$ subcubes. This special case can still simulate many other hard learning problems, but is much richer than any of them alone. As a corollary, we obtain more flexible algorithms for learning decision trees under the uniform distribution, that work with stochastic transitions, when we are only given positive examples and with a polylogarithmic number of samples for any fixed $k$. Our algorithms are based on a win-win analysis where we either build a basis for the moments or locate a degeneracy that can be used to simplify the problem, which we believe will have applications to other learning problems over discrete domains.

Being Robust (in High Dimensions) Can Be Practical

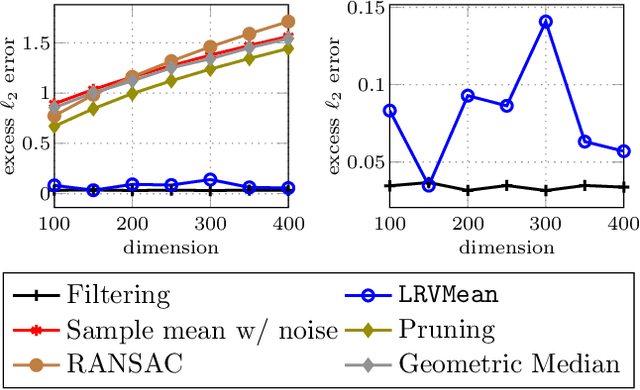
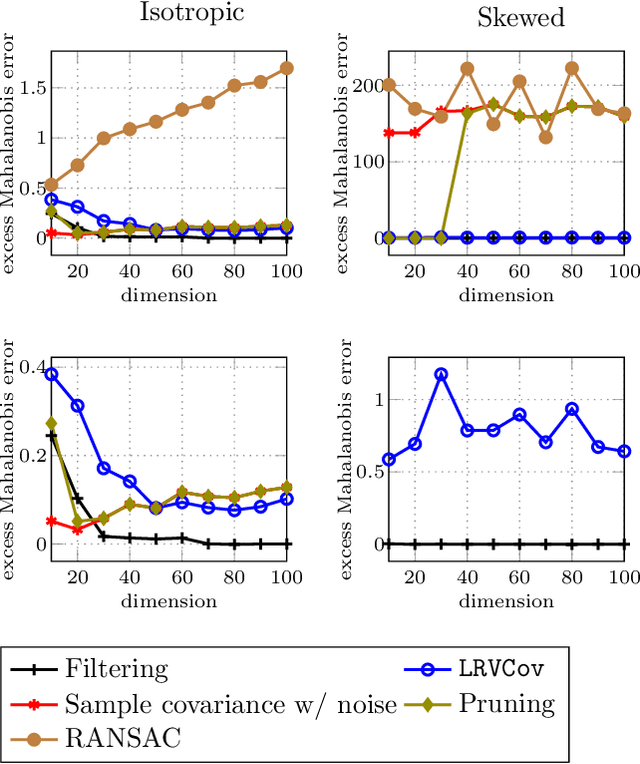
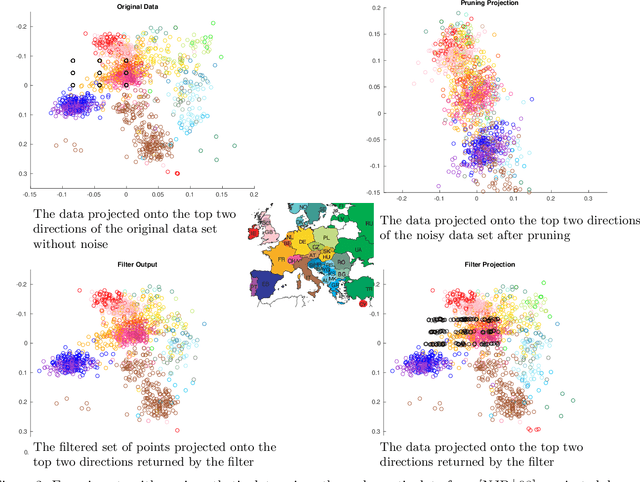
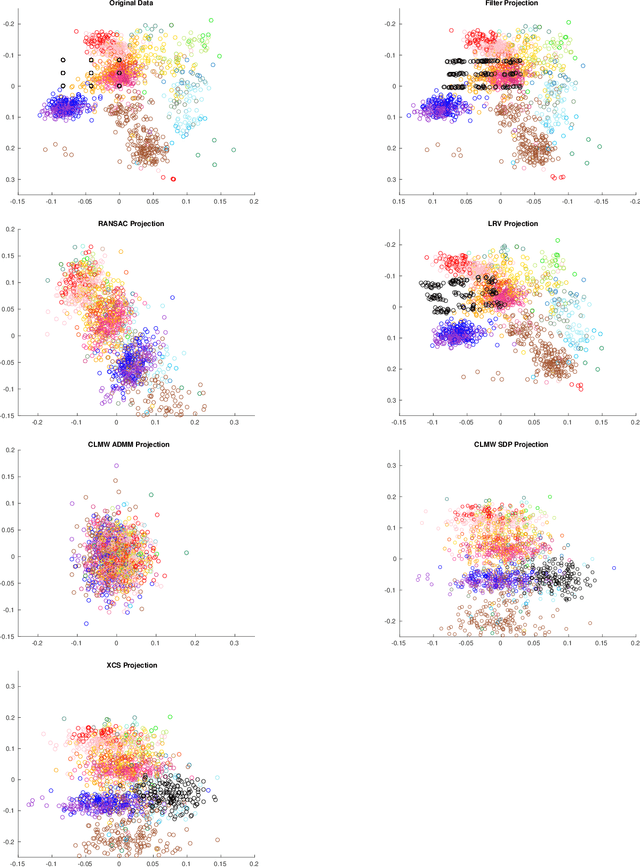
Robust estimation is much more challenging in high dimensions than it is in one dimension: Most techniques either lead to intractable optimization problems or estimators that can tolerate only a tiny fraction of errors. Recent work in theoretical computer science has shown that, in appropriate distributional models, it is possible to robustly estimate the mean and covariance with polynomial time algorithms that can tolerate a constant fraction of corruptions, independent of the dimension. However, the sample and time complexity of these algorithms is prohibitively large for high-dimensional applications. In this work, we address both of these issues by establishing sample complexity bounds that are optimal, up to logarithmic factors, as well as giving various refinements that allow the algorithms to tolerate a much larger fraction of corruptions. Finally, we show on both synthetic and real data that our algorithms have state-of-the-art performance and suddenly make high-dimensional robust estimation a realistic possibility.

Robustly Learning a Gaussian: Getting Optimal Error, Efficiently

We study the fundamental problem of learning the parameters of a high-dimensional Gaussian in the presence of noise -- where an $\varepsilon$-fraction of our samples were chosen by an adversary. We give robust estimators that achieve estimation error $O(\varepsilon)$ in the total variation distance, which is optimal up to a universal constant that is independent of the dimension. In the case where just the mean is unknown, our robustness guarantee is optimal up to a factor of $\sqrt{2}$ and the running time is polynomial in $d$ and $1/\epsilon$. When both the mean and covariance are unknown, the running time is polynomial in $d$ and quasipolynomial in $1/\varepsilon$. Moreover all of our algorithms require only a polynomial number of samples. Our work shows that the same sorts of error guarantees that were established over fifty years ago in the one-dimensional setting can also be achieved by efficient algorithms in high-dimensional settings.

Information Theoretic Properties of Markov Random Fields, and their Algorithmic Applications

Markov random fields area popular model for high-dimensional probability distributions. Over the years, many mathematical, statistical and algorithmic problems on them have been studied. Until recently, the only known algorithms for provably learning them relied on exhaustive search, correlation decay or various incoherence assumptions. Bresler gave an algorithm for learning general Ising models on bounded degree graphs. His approach was based on a structural result about mutual information in Ising models. Here we take a more conceptual approach to proving lower bounds on the mutual information through setting up an appropriate zero-sum game. Our proof generalizes well beyond Ising models, to arbitrary Markov random fields with higher order interactions. As an application, we obtain algorithms for learning Markov random fields on bounded degree graphs on $n$ nodes with $r$-order interactions in $n^r$ time and $\log n$ sample complexity. The sample complexity is information theoretically optimal up to the dependence on the maximum degree. The running time is nearly optimal under standard conjectures about the hardness of learning parity with noise.

Approximate Counting, the Lovasz Local Lemma and Inference in Graphical Models

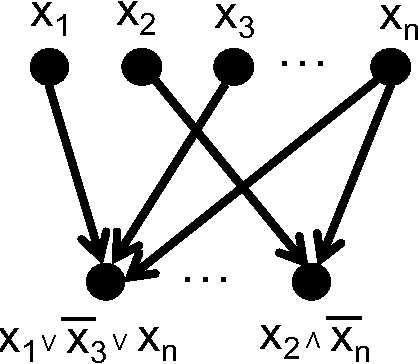
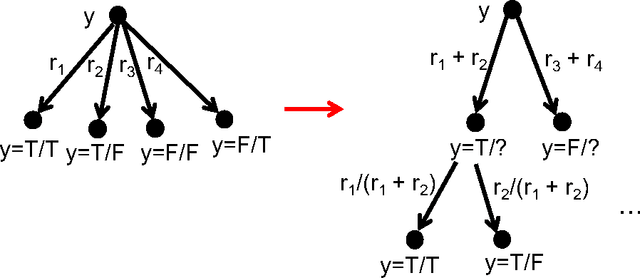
In this paper we introduce a new approach for approximately counting in bounded degree systems with higher-order constraints. Our main result is an algorithm to approximately count the number of solutions to a CNF formula $\Phi$ when the width is logarithmic in the maximum degree. This closes an exponential gap between the known upper and lower bounds. Moreover our algorithm extends straightforwardly to approximate sampling, which shows that under Lov\'asz Local Lemma-like conditions it is not only possible to find a satisfying assignment, it is also possible to generate one approximately uniformly at random from the set of all satisfying assignments. Our approach is a significant departure from earlier techniques in approximate counting, and is based on a framework to bootstrap an oracle for computing marginal probabilities on individual variables. Finally, we give an application of our results to show that it is algorithmically possible to sample from the posterior distribution in an interesting class of graphical models.

Optimality and Sub-optimality of PCA for Spiked Random Matrices and Synchronization

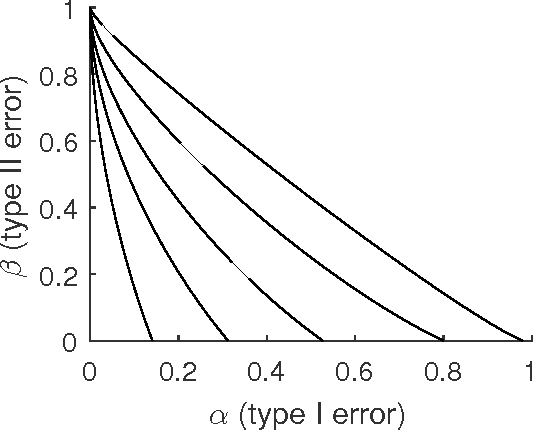
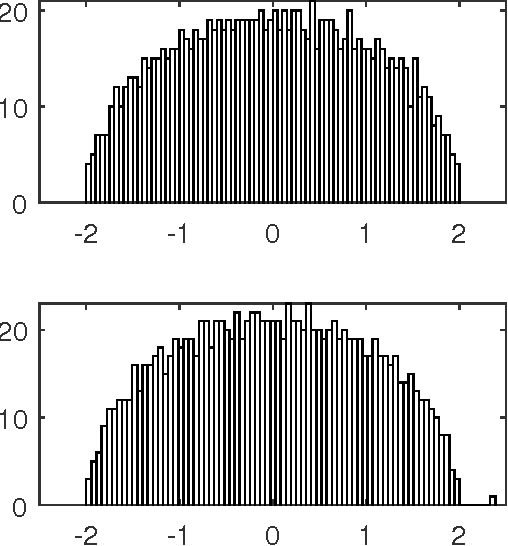
A central problem of random matrix theory is to understand the eigenvalues of spiked random matrix models, in which a prominent eigenvector is planted into a random matrix. These distributions form natural statistical models for principal component analysis (PCA) problems throughout the sciences. Baik, Ben Arous and P\'ech\'e showed that the spiked Wishart ensemble exhibits a sharp phase transition asymptotically: when the signal strength is above a critical threshold, it is possible to detect the presence of a spike based on the top eigenvalue, and below the threshold the top eigenvalue provides no information. Such results form the basis of our understanding of when PCA can detect a low-rank signal in the presence of noise. However, not all the information about the spike is necessarily contained in the spectrum. We study the fundamental limitations of statistical methods, including non-spectral ones. Our results include: I) For the Gaussian Wigner ensemble, we show that PCA achieves the optimal detection threshold for a variety of benign priors for the spike. We extend previous work on the spherically symmetric and i.i.d. Rademacher priors through an elementary, unified analysis. II) For any non-Gaussian Wigner ensemble, we show that PCA is always suboptimal for detection. However, a variant of PCA achieves the optimal threshold (for benign priors) by pre-transforming the matrix entries according to a carefully designed function. This approach has been stated before, and we give a rigorous and general analysis. III) For both the Gaussian Wishart ensemble and various synchronization problems over groups, we show that inefficient procedures can work below the threshold where PCA succeeds, whereas no known efficient algorithm achieves this. This conjectural gap between what is statistically possible and what can be done efficiently remains open.

Message-passing algorithms for synchronization problems over compact groups

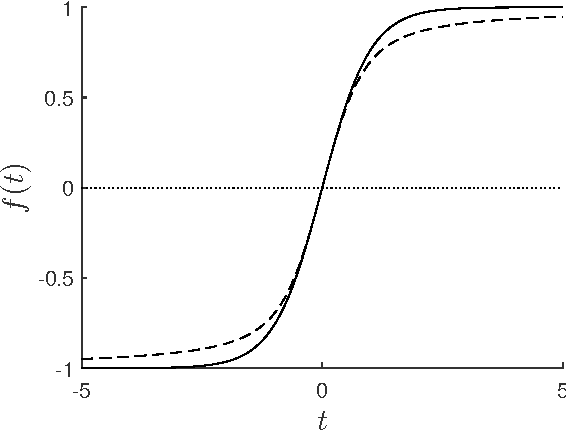
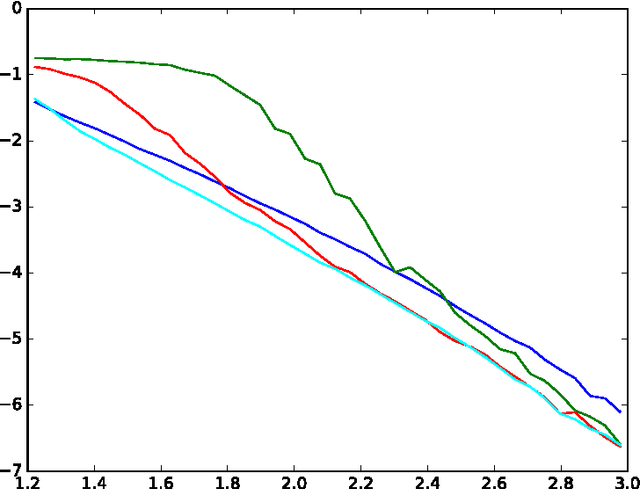
Various alignment problems arising in cryo-electron microscopy, community detection, time synchronization, computer vision, and other fields fall into a common framework of synchronization problems over compact groups such as Z/L, U(1), or SO(3). The goal of such problems is to estimate an unknown vector of group elements given noisy relative observations. We present an efficient iterative algorithm to solve a large class of these problems, allowing for any compact group, with measurements on multiple 'frequency channels' (Fourier modes, or more generally, irreducible representations of the group). Our algorithm is a highly efficient iterative method following the blueprint of approximate message passing (AMP), which has recently arisen as a central technique for inference problems such as structured low-rank estimation and compressed sensing. We augment the standard ideas of AMP with ideas from representation theory so that the algorithm can work with distributions over compact groups. Using standard but non-rigorous methods from statistical physics we analyze the behavior of our algorithm on a Gaussian noise model, identifying phases where the problem is easy, (computationally) hard, and (statistically) impossible. In particular, such evidence predicts that our algorithm is information-theoretically optimal in many cases, and that the remaining cases show evidence of statistical-to-computational gaps.

Provable Algorithms for Inference in Topic Models

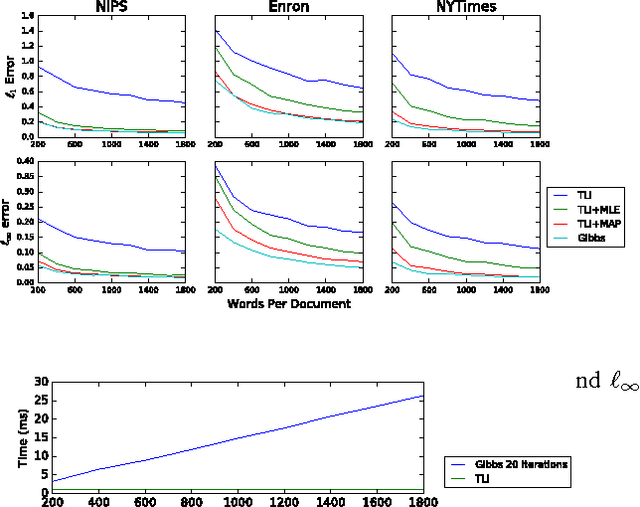
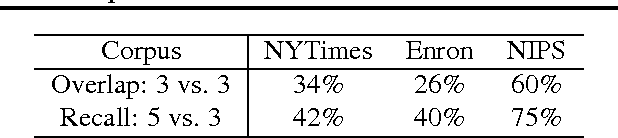
Recently, there has been considerable progress on designing algorithms with provable guarantees -- typically using linear algebraic methods -- for parameter learning in latent variable models. But designing provable algorithms for inference has proven to be more challenging. Here we take a first step towards provable inference in topic models. We leverage a property of topic models that enables us to construct simple linear estimators for the unknown topic proportions that have small variance, and consequently can work with short documents. Our estimators also correspond to finding an estimate around which the posterior is well-concentrated. We show lower bounds that for shorter documents it can be information theoretically impossible to find the hidden topics. Finally, we give empirical results that demonstrate that our algorithm works on realistic topic models. It yields good solutions on synthetic data and runs in time comparable to a {\em single} iteration of Gibbs sampling.