Online and Distribution-Free Robustness: Regression and Contextual Bandits with Huber Contamination

In this work we revisit two classic high-dimensional online learning problems, namely regression and linear contextual bandits, from the perspective of adversarial robustness. Existing works in algorithmic robust statistics make strong distributional assumptions that ensure that the input data is evenly spread out or comes from a nice generative model. Is it possible to achieve strong robustness guarantees even without distributional assumptions altogether, where the sequence of tasks we are asked to solve is adaptively and adversarially chosen? We answer this question in the affirmative for both regression and linear contextual bandits. In fact our algorithms succeed where convex surrogates fail in the sense that we show strong lower bounds categorically for the existing approaches. Our approach is based on a novel way to use the sum-of-squares hierarchy in online learning and in the absence of distributional assumptions. Moreover we give extensions of our main results to infinite dimensional settings where the feature vectors are represented implicitly via a kernel map.

Classification Under Misspecification: Halfspaces, Generalized Linear Models, and Connections to Evolvability

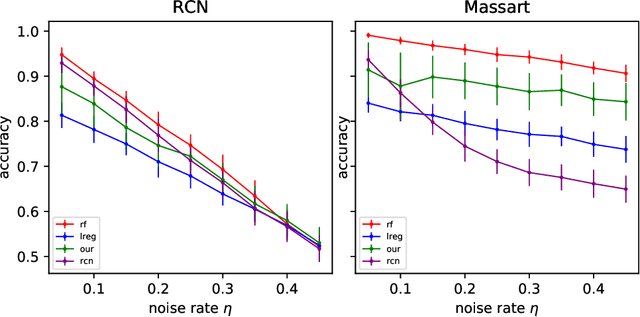
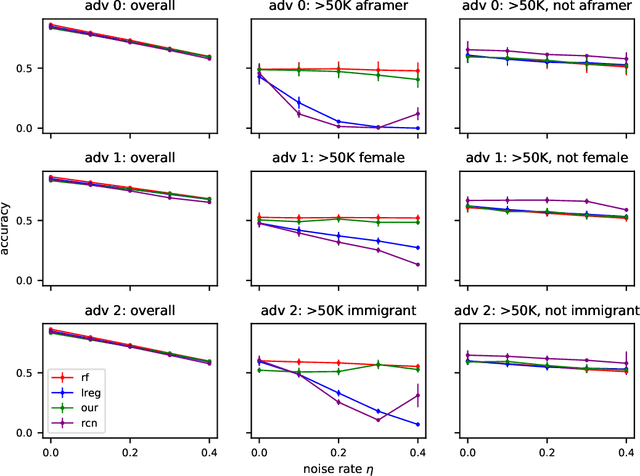
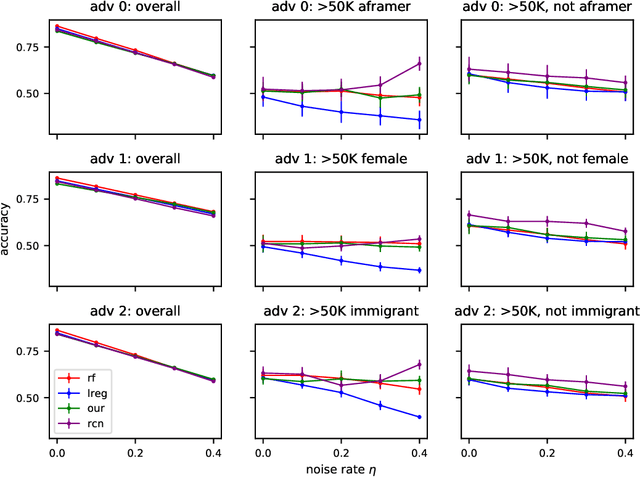
In this paper we revisit some classic problems on classification under misspecification. In particular, we study the problem of learning halfspaces under Massart noise with rate $\eta$. In a recent work, Diakonikolas, Goulekakis, and Tzamos resolved a long-standing problem by giving the first efficient algorithm for learning to accuracy $\eta + \epsilon$ for any $\epsilon > 0$. However, their algorithm outputs a complicated hypothesis, which partitions space into $\text{poly}(d,1/\epsilon)$ regions. Here we give a much simpler algorithm and in the process resolve a number of outstanding open questions: (1) We give the first proper learner for Massart halfspaces that achieves $\eta + \epsilon$. We also give improved bounds on the sample complexity achievable by polynomial time algorithms. (2) Based on (1), we develop a blackbox knowledge distillation procedure to convert an arbitrarily complex classifier to an equally good proper classifier. (3) By leveraging a simple but overlooked connection to evolvability, we show any SQ algorithm requires super-polynomially many queries to achieve $\mathsf{OPT} + \epsilon$. Moreover we study generalized linear models where $\mathbb{E}[Y|\mathbf{X}] = \sigma(\langle \mathbf{w}^*, \mathbf{X}\rangle)$ for any odd, monotone, and Lipschitz function $\sigma$. This family includes the previously mentioned halfspace models as a special case, but is much richer and includes other fundamental models like logistic regression. We introduce a challenging new corruption model that generalizes Massart noise, and give a general algorithm for learning in this setting. Our algorithms are based on a small set of core recipes for learning to classify in the presence of misspecification. Finally we study our algorithm for learning halfspaces under Massart noise empirically and find that it exhibits some appealing fairness properties.

Tensor Completion Made Practical

Tensor completion is a natural higher-order generalization of matrix completion where the goal is to recover a low-rank tensor from sparse observations of its entries. Existing algorithms are either heuristic without provable guarantees, based on solving large semidefinite programs which are impractical to run, or make strong assumptions such as requiring the factors to be nearly orthogonal. In this paper we introduce a new variant of alternating minimization, which in turn is inspired by understanding how the progress measures that guide convergence of alternating minimization in the matrix setting need to be adapted to the tensor setting. We show strong provable guarantees, including showing that our algorithm converges linearly to the true tensors even when the factors are highly correlated and can be implemented in nearly linear time. Moreover our algorithm is also highly practical and we show that we can complete third order tensors with a thousand dimensions from observing a tiny fraction of its entries. In contrast, and somewhat surprisingly, we show that the standard version of alternating minimization, without our new twist, can converge at a drastically slower rate in practice.

Learning Structured Distributions From Untrusted Batches: Faster and Simpler

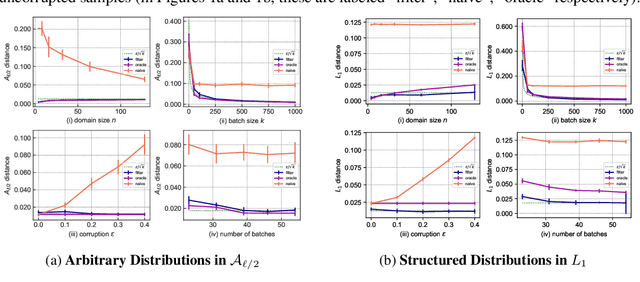
We revisit the problem of learning from untrusted batches introduced by Qiao and Valiant [QV17]. Recently, Jain and Orlitsky [JO19] gave a simple semidefinite programming approach based on the cut-norm that achieves essentially information-theoretically optimal error in polynomial time. Concurrently, Chen et al. [CLM19] considered a variant of the problem where $\mu$ is assumed to be structured, e.g. log-concave, monotone hazard rate, $t$-modal, etc. In this case, it is possible to achieve the same error with sample complexity sublinear in $n$, and they exhibited a quasi-polynomial time algorithm for doing so using Haar wavelets. In this paper, we find an appealing way to synthesize the techniques of [JO19] and [CLM19] to give the best of both worlds: an algorithm which runs in polynomial time and can exploit structure in the underlying distribution to achieve sublinear sample complexity. Along the way, we simplify the approach of [JO19] by avoiding the need for SDP rounding and giving a more direct interpretation of it through the lens of soft filtering, a powerful recent technique in high-dimensional robust estimation.

Fast Convergence for Langevin Diffusion with Matrix Manifold Structure

In this paper, we study the problem of sampling from distributions of the form p(x) \propto e^{-\beta f(x)} for some function f whose values and gradients we can query. This mode of access to f is natural in the scenarios in which such problems arise, for instance sampling from posteriors in parametric Bayesian models. Classical results show that a natural random walk, Langevin diffusion, mixes rapidly when f is convex. Unfortunately, even in simple examples, the applications listed above will entail working with functions f that are nonconvex -- for which sampling from p may in general require an exponential number of queries. In this paper, we study one aspect of nonconvexity relevant for modern machine learning applications: existence of invariances (symmetries) in the function f, as a result of which the distribution p will have manifolds of points with equal probability. We give a recipe for proving mixing time bounds of Langevin dynamics in order to sample from manifolds of local optima of the function f in settings where the distribution is well-concentrated around them. We specialize our arguments to classic matrix factorization-like Bayesian inference problems where we get noisy measurements A(XX^T), X \in R^{d \times k} of a low-rank matrix, i.e. f(X) = \|A(XX^T) - b\|^2_2, X \in R^{d \times k}, and \beta the inverse of the variance of the noise. Such functions f are invariant under orthogonal transformations, and include problems like matrix factorization, sensing, completion. Beyond sampling, Langevin dynamics is a popular toy model for studying stochastic gradient descent. Along these lines, we believe that our work is an important first step towards understanding how SGD behaves when there is a high degree of symmetry in the space of parameters the produce the same output.

Polynomial time guarantees for the Burer-Monteiro method

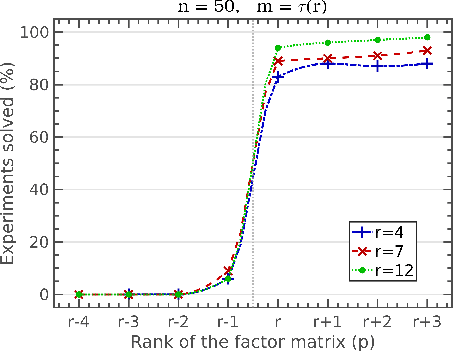
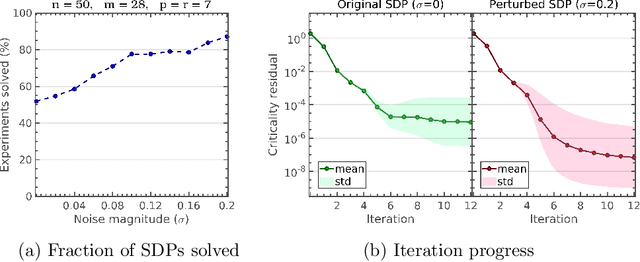
The Burer-Monteiro method is one of the most widely used techniques for solving large-scale semidefinite programs (SDP). The basic idea is to solve a nonconvex program in $Y$, where $Y$ is an $n \times p$ matrix such that $X = Y Y^T$. In this paper, we show that this method can solve SDPs in polynomial time in an smoothed analysis setting. More precisely, we consider an SDP whose domain satisfies some compactness and smoothness assumptions, and slightly perturb the cost matrix and the constraints. We show that if $p \gtrsim \sqrt{2(1+\eta)m}$, where $m$ is the number of constraints and $\eta>0$ is any fixed constant, then the Burer-Monteiro method can solve SDPs to any desired accuracy in polynomial time, in the setting of smooth analysis. Our bound on $p$ approaches the celebrated Barvinok-Pataki bound in the limit as $\eta$ goes to zero, beneath which it is known that the nonconvex program can be suboptimal. Previous analyses were unable to give polynomial time guarantees for the Burer-Monteiro method, since they either assumed that the criticality conditions are satisfied exactly, or ignored the nontrivial problem of computing an approximately feasible solution. We address the first problem through a novel connection with tubular neighborhoods of algebraic varieties. For the feasibility problem we consider a least squares formulation, and provide the first guarantees that do not rely on the restricted isometry property.

Efficiently Learning Structured Distributions from Untrusted Batches

We study the problem, introduced by Qiao and Valiant, of learning from untrusted batches. Here, we assume $m$ users, all of whom have samples from some underlying distribution $p$ over $1, \ldots, n$. Each user sends a batch of $k$ i.i.d. samples from this distribution; however an $\epsilon$-fraction of users are untrustworthy and can send adversarially chosen responses. The goal is then to learn $p$ in total variation distance. When $k = 1$ this is the standard robust univariate density estimation setting and it is well-understood that $\Omega (\epsilon)$ error is unavoidable. Suprisingly, Qiao and Valiant gave an estimator which improves upon this rate when $k$ is large. Unfortunately, their algorithms run in time exponential in either $n$ or $k$. We first give a sequence of polynomial time algorithms whose estimation error approaches the information-theoretically optimal bound for this problem. Our approach is based on recent algorithms derived from the sum-of-squares hierarchy, in the context of high-dimensional robust estimation. We show that algorithms for learning from untrusted batches can also be cast in this framework, but by working with a more complicated set of test functions. It turns out this abstraction is quite powerful and can be generalized to incorporate additional problem specific constraints. Our second and main result is to show that this technology can be leveraged to build in prior knowledge about the shape of the distribution. Crucially, this allows us to reduce the sample complexity of learning from untrusted batches to polylogarithmic in $n$ for most natural classes of distributions, which is important in many applications. To do so, we demonstrate that these sum-of-squares algorithms for robust mean estimation can be made to handle complex combinatorial constraints (e.g. those arising from VC theory), which may be of independent technical interest.

Learning Some Popular Gaussian Graphical Models without Condition Number Bounds

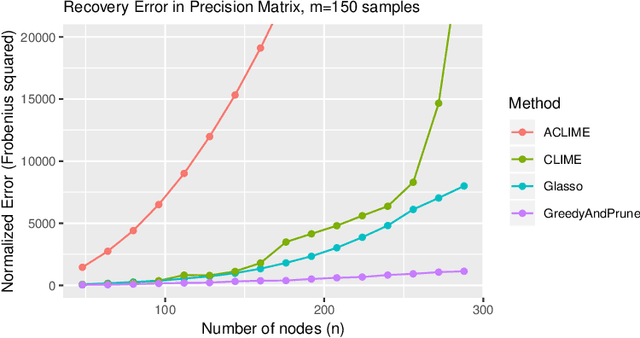
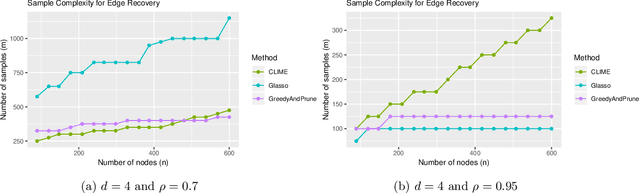
Gaussian Graphical Models (GGMs) have wide-ranging applications in machine learning and the natural and social sciences. In most of the settings in which they are applied, the number of observed samples is much smaller than the dimension and they are assumed to be sparse. While there are a variety of algorithms (e.g. Graphical Lasso, CLIME) that provably recover the graph structure with a logarithmic number of samples, they assume various conditions that require the precision matrix to be in some sense well-conditioned. Here we give the first polynomial-time algorithms for learning attractive GGMs and walk-summable GGMs with a logarithmic number of samples without any such assumptions. In particular, our algorithms can tolerate strong dependencies among the variables. We complement our results with experiments showing that many existing algorithms fail even in some simple settings where there are long dependency chains, whereas ours do not.

Learning Restricted Boltzmann Machines via Influence Maximization

Graphical models are a rich language for describing high-dimensional distributions in terms of their dependence structure. While there are algorithms with provable guarantees for learning undirected graphical models in a variety of settings, there has been much less progress in the important scenario when there are latent variables. Here we study Restricted Boltzmann Machines (or RBMs), which are a popular model with wide-ranging applications in dimensionality reduction, collaborative filtering, topic modeling, feature extraction and deep learning. The main message of our paper is a strong dichotomy in the feasibility of learning RBMs, depending on the nature of the interactions between variables: ferromagnetic models can be learned efficiently, while general models cannot. In particular, we give a simple greedy algorithm based on influence maximization to learn ferromagnetic RBMs with bounded degree. In fact, we learn a description of the distribution on the observed variables as a Markov Random Field. Our analysis is based on tools from mathematical physics that were developed to show the concavity of magnetization. Our algorithm extends straighforwardly to general ferromagnetic Ising models with latent variables. Conversely, we show that even for a contant number of latent variables with constant degree, without ferromagneticity the problem is as hard as sparse parity with noise. This hardness result is based on a sharp and surprising characterization of the representational power of bounded degree RBMs: the distribution on their observed variables can simulate any bounded order MRF. This result is of independent interest since RBMs are the building blocks of deep belief networks.

Spectral Methods from Tensor Networks

A tensor network is a diagram that specifies a way to "multiply" a collection of tensors together to produce another tensor (or matrix). Many existing algorithms for tensor problems (such as tensor decomposition and tensor PCA), although they are not presented this way, can be viewed as spectral methods on matrices built from simple tensor networks. In this work we leverage the full power of this abstraction to design new algorithms for certain continuous tensor decomposition problems. An important and challenging family of tensor problems comes from orbit recovery, a class of inference problems involving group actions (inspired by applications such as cryo-electron microscopy). Orbit recovery problems over finite groups can often be solved via standard tensor methods. However, for infinite groups, no general algorithms are known. We give a new spectral algorithm based on tensor networks for one such problem: continuous multi-reference alignment over the infinite group SO(2). Our algorithm extends to the more general heterogeneous case.