Robust Voting Rules from Algorithmic Robust Statistics

In this work we study the problem of robustly learning a Mallows model. We give an algorithm that can accurately estimate the central ranking even when a constant fraction of its samples are arbitrarily corrupted. Moreover our robustness guarantees are dimension-independent in the sense that our overall accuracy does not depend on the number of alternatives being ranked. Our work can be thought of as a natural infusion of perspectives from algorithmic robust statistics into one of the central inference problems in voting and information-aggregation. Specifically, our voting rule is efficiently computable and its outcome cannot be changed by much by a large group of colluding voters.

Kalman Filtering with Adversarial Corruptions

Here we revisit the classic problem of linear quadratic estimation, i.e. estimating the trajectory of a linear dynamical system from noisy measurements. The celebrated Kalman filter gives an optimal estimator when the measurement noise is Gaussian, but is widely known to break down when one deviates from this assumption, e.g. when the noise is heavy-tailed. Many ad hoc heuristics have been employed in practice for dealing with outliers. In a pioneering work, Schick and Mitter gave provable guarantees when the measurement noise is a known infinitesimal perturbation of a Gaussian and raised the important question of whether one can get similar guarantees for large and unknown perturbations. In this work we give a truly robust filter: we give the first strong provable guarantees for linear quadratic estimation when even a constant fraction of measurements have been adversarially corrupted. This framework can model heavy-tailed and even non-stationary noise processes. Our algorithm robustifies the Kalman filter in the sense that it competes with the optimal algorithm that knows the locations of the corruptions. Our work is in a challenging Bayesian setting where the number of measurements scales with the complexity of what we need to estimate. Moreover, in linear dynamical systems past information decays over time. We develop a suite of new techniques to robustly extract information across different time steps and over varying time scales.

Can Q-Learning be Improved with Advice?

Despite rapid progress in theoretical reinforcement learning (RL) over the last few years, most of the known guarantees are worst-case in nature, failing to take advantage of structure that may be known a priori about a given RL problem at hand. In this paper we address the question of whether worst-case lower bounds for regret in online learning of Markov decision processes (MDPs) can be circumvented when information about the MDP, in the form of predictions about its optimal $Q$-value function, is given to the algorithm. We show that when the predictions about the optimal $Q$-value function satisfy a reasonably weak condition we call distillation, then we can improve regret bounds by replacing the set of state-action pairs with the set of state-action pairs on which the predictions are grossly inaccurate. This improvement holds for both uniform regret bounds and gap-based ones. Further, we are able to achieve this property with an algorithm that achieves sublinear regret when given arbitrary predictions (i.e., even those which are not a distillation). Our work extends a recent line of work on algorithms with predictions, which has typically focused on simple online problems such as caching and scheduling, to the more complex and general problem of reinforcement learning.

Spoofing Generalization: When Can't You Trust Proprietary Models?

In this work, we study the computational complexity of determining whether a machine learning model that perfectly fits the training data will generalizes to unseen data. In particular, we study the power of a malicious agent whose goal is to construct a model g that fits its training data and nothing else, but is indistinguishable from an accurate model f. We say that g strongly spoofs f if no polynomial-time algorithm can tell them apart. If instead we restrict to algorithms that run in $n^c$ time for some fixed $c$, we say that g c-weakly spoofs f. Our main results are 1. Under cryptographic assumptions, strong spoofing is possible and 2. For any c> 0, c-weak spoofing is possible unconditionally While the assumption of a malicious agent is an extreme scenario (hopefully companies training large models are not malicious), we believe that it sheds light on the inherent difficulties of blindly trusting large proprietary models or data.

Sparsification for Sums of Exponentials and its Algorithmic Applications

Many works in signal processing and learning theory operate under the assumption that the underlying model is simple, e.g. that a signal is approximately $k$-Fourier-sparse or that a distribution can be approximated by a mixture model that has at most $k$ components. However the problem of fitting the parameters of such a model becomes more challenging when the frequencies/components are too close together. In this work we introduce new methods for sparsifying sums of exponentials and give various algorithmic applications. First we study Fourier-sparse interpolation without a frequency gap, where Chen et al. gave an algorithm for finding an $\epsilon$-approximate solution which uses $k' = \mbox{poly}(k, \log 1/\epsilon)$ frequencies. Second, we study learning Gaussian mixture models in one dimension without a separation condition. Kernel density estimators give an $\epsilon$-approximation that uses $k' = O(k/\epsilon^2)$ components. These methods both output models that are much more complex than what we started out with. We show how to post-process to reduce the number of frequencies/components down to $k' = \widetilde{O}(k)$, which is optimal up to logarithmic factors. Moreover we give applications to model selection. In particular, we give the first algorithms for approximately (and robustly) determining the number of components in a Gaussian mixture model that work without a separation condition.

How to Decompose a Tensor with Group Structure

In this work we study the orbit recovery problem, which is a natural abstraction for the problem of recovering a planted signal from noisy measurements under unknown group actions. Many important inverse problems in statistics, engineering and the sciences fit into this framework. Prior work has studied cases when the group is discrete and/or abelian. However fundamentally new techniques are needed in order to handle more complex group actions. Our main result is a quasi-polynomial time algorithm to solve orbit recovery over $SO(3)$ - i.e. the cryo-electron tomography problem which asks to recover the three-dimensional structure of a molecule from noisy measurements of randomly rotated copies of it. We analyze a variant of the frequency marching heuristic in the framework of smoothed analysis. Our approach exploits the layered structure of the invariant polynomials, and simultaneously yields a new class of tensor decomposition algorithms that work in settings when the tensor is not low-rank but rather where the factors are algebraically related to each other by a group action.

Learning GMMs with Nearly Optimal Robustness Guarantees

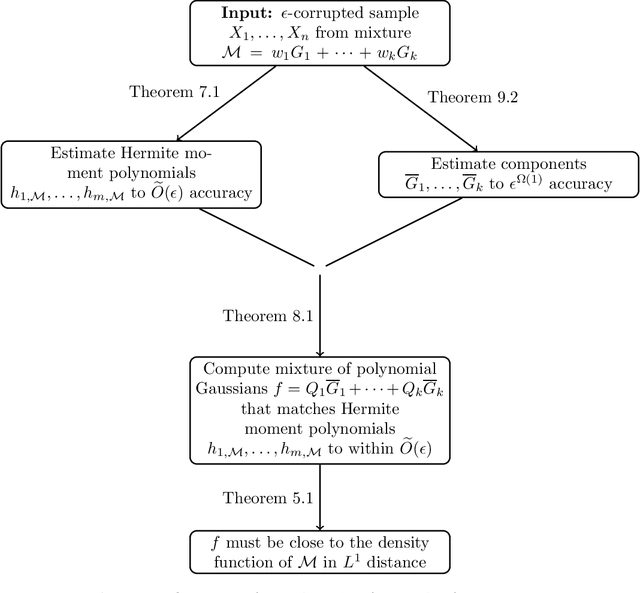
In this work we solve the problem of robustly learning a high-dimensional Gaussian mixture model with $k$ components from $\epsilon$-corrupted samples up to accuracy $\widetilde{O}(\epsilon)$ in total variation distance for any constant $k$ and with mild assumptions on the mixture. This robustness guarantee is optimal up to polylogarithmic factors. At the heart of our algorithm is a new way to relax a system of polynomial equations which corresponds to solving an improper learning problem where we are allowed to output a Gaussian mixture model whose weights are low-degree polynomials.

No-go Theorem for Acceleration in the Hyperbolic Plane

In recent years there has been significant effort to adapt the key tools and ideas in convex optimization to the Riemannian setting. One key challenge has remained: Is there a Nesterov-like accelerated gradient method for geodesically convex functions on a Riemannian manifold? Recent work has given partial answers and the hope was that this ought to be possible. Here we dash these hopes. We prove that in a noisy setting, there is no analogue of accelerated gradient descent for geodesically convex functions on the hyperbolic plane. Our results apply even when the noise is exponentially small. The key intuition behind our proof is short and simple: In negatively curved spaces, the volume of a ball grows so fast that information about the past gradients is not useful in the future.

Learning to Sample from Censored Markov Random Fields

We study learning Censor Markov Random Fields (abbreviated CMRFs). These are Markov Random Fields where some of the nodes are censored (not observed). We present an algorithm for learning high-temperature CMRFs within o(n) transportation distance. Crucially our algorithm makes no assumption about the structure of the graph or the number or location of the observed nodes. We obtain stronger results for high girth high-temperature CMRFs as well as computational lower bounds indicating that our results can not be qualitatively improved.

Settling the Robust Learnability of Mixtures of Gaussians

This work represents a natural coalescence of two important lines of work: learning mixtures of Gaussians and algorithmic robust statistics. In particular we give the first provably robust algorithm for learning mixtures of any constant number of Gaussians. We require only mild assumptions on the mixing weights (bounded fractionality) and that the total variation distance between components is bounded away from zero. At the heart of our algorithm is a new method for proving dimension-independent polynomial identifiability through applying a carefully chosen sequence of differential operations to certain generating functions that not only encode the parameters we would like to learn but also the system of polynomial equations we would like to solve. We show how the symbolic identities we derive can be directly used to analyze a natural sum-of-squares relaxation.