Colin Sandon
How Far Can Transformers Reason? The Locality Barrier and Inductive Scratchpad
Jun 10, 2024



Abstract:Can Transformers predict new syllogisms by composing established ones? More generally, what type of targets can be learned by such models from scratch? Recent works show that Transformers can be Turing-complete in terms of expressivity, but this does not address the learnability objective. This paper puts forward the notion of 'distribution locality' to capture when weak learning is efficiently achievable by regular Transformers, where the locality measures the least number of tokens required in addition to the tokens histogram to correlate nontrivially with the target. As shown experimentally and theoretically under additional assumptions, distributions with high locality cannot be learned efficiently. In particular, syllogisms cannot be composed on long chains. Furthermore, we show that (i) an agnostic scratchpad cannot help to break the locality barrier, (ii) an educated scratchpad can help if it breaks the locality at each step, (iii) a notion of 'inductive scratchpad' can both break the locality and improve the out-of-distribution generalization, e.g., generalizing to almost double input size for some arithmetic tasks.
Spectral Algorithms Optimally Recover (Censored) Planted Dense Subgraphs
Mar 22, 2022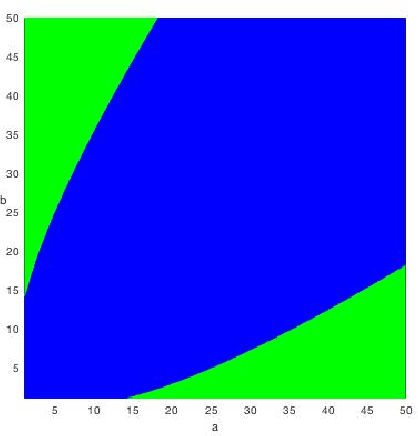
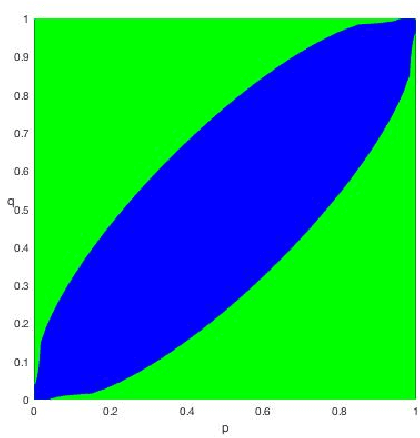
Abstract:We study spectral algorithms for the planted dense subgraph problem (PDS), as well as for a censored variant (CPDS) of PDS, where the edge statuses are missing at random. More precisely, in the PDS model, we consider $n$ vertices and a random subset of vertices $S^{\star}$ of size $\Omega(n)$, such that two vertices share an edge with probability $p$ if both of them are in $S^{\star}$, and all other edges are present with probability $q$, independently. The goal is to recover $S^{\star}$ from one observation of the network. In the CPDS model, edge statuses are revealed with probability $\frac{t \log n}{n}$. For the PDS model, we show that a simple spectral algorithm based on the top two eigenvectors of the adjacency matrix can recover $S^{\star}$ up to the information theoretic threshold. Prior work by Hajek, Wu and Xu required a less efficient SDP based algorithm to recover $S^{\star}$ up to the information theoretic threshold. For the CDPS model, we obtain the information theoretic limit for the recovery problem, and further show that a spectral algorithm based on a special matrix called the signed adjacency matrix recovers $S^{\star}$ up to the information theoretic threshold.
On the Power of Differentiable Learning versus PAC and SQ Learning
Aug 09, 2021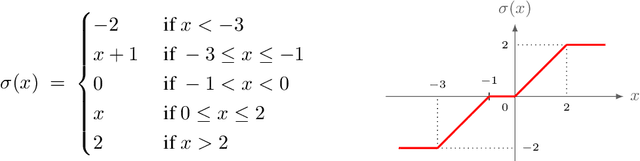
Abstract:We study the power of learning via mini-batch stochastic gradient descent (SGD) on the population loss, and batch Gradient Descent (GD) on the empirical loss, of a differentiable model or neural network, and ask what learning problems can be learnt using these paradigms. We show that SGD and GD can always simulate learning with statistical queries (SQ), but their ability to go beyond that depends on the precision $\rho$ of the gradient calculations relative to the minibatch size $b$ (for SGD) and sample size $m$ (for GD). With fine enough precision relative to minibatch size, namely when $b \rho$ is small enough, SGD can go beyond SQ learning and simulate any sample-based learning algorithm and thus its learning power is equivalent to that of PAC learning; this extends prior work that achieved this result for $b=1$. Similarly, with fine enough precision relative to the sample size $m$, GD can also simulate any sample-based learning algorithm based on $m$ samples. In particular, with polynomially many bits of precision (i.e. when $\rho$ is exponentially small), SGD and GD can both simulate PAC learning regardless of the mini-batch size. On the other hand, when $b \rho^2$ is large enough, the power of SGD is equivalent to that of SQ learning.
Spoofing Generalization: When Can't You Trust Proprietary Models?
Jun 15, 2021Abstract:In this work, we study the computational complexity of determining whether a machine learning model that perfectly fits the training data will generalizes to unseen data. In particular, we study the power of a malicious agent whose goal is to construct a model g that fits its training data and nothing else, but is indistinguishable from an accurate model f. We say that g strongly spoofs f if no polynomial-time algorithm can tell them apart. If instead we restrict to algorithms that run in $n^c$ time for some fixed $c$, we say that g c-weakly spoofs f. Our main results are 1. Under cryptographic assumptions, strong spoofing is possible and 2. For any c> 0, c-weak spoofing is possible unconditionally While the assumption of a malicious agent is an extreme scenario (hopefully companies training large models are not malicious), we believe that it sheds light on the inherent difficulties of blindly trusting large proprietary models or data.
Learning to Sample from Censored Markov Random Fields
Jan 15, 2021Abstract:We study learning Censor Markov Random Fields (abbreviated CMRFs). These are Markov Random Fields where some of the nodes are censored (not observed). We present an algorithm for learning high-temperature CMRFs within o(n) transportation distance. Crucially our algorithm makes no assumption about the structure of the graph or the number or location of the observed nodes. We obtain stronger results for high girth high-temperature CMRFs as well as computational lower bounds indicating that our results can not be qualitatively improved.
Poly-time universality and limitations of deep learning
Jan 07, 2020
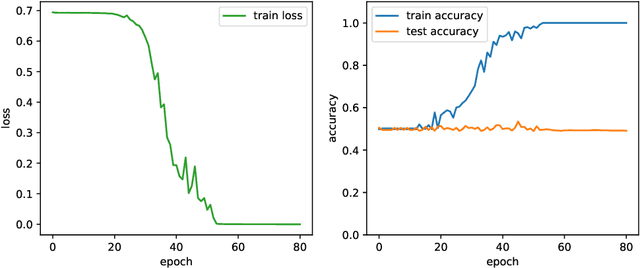
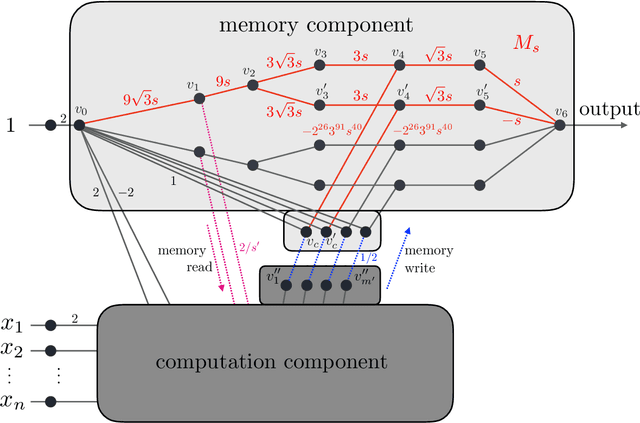
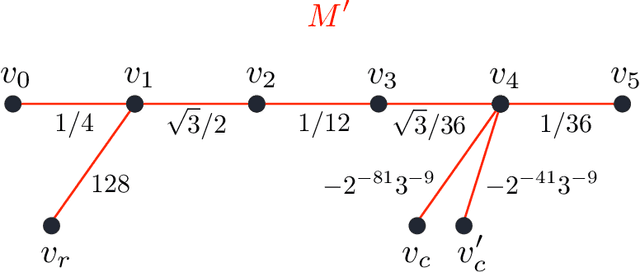
Abstract:The goal of this paper is to characterize function distributions that deep learning can or cannot learn in poly-time. A universality result is proved for SGD-based deep learning and a non-universality result is proved for GD-based deep learning; this also gives a separation between SGD-based deep learning and statistical query algorithms: (1) {\it Deep learning with SGD is efficiently universal.} Any function distribution that can be learned from samples in poly-time can also be learned by a poly-size neural net trained with SGD on a poly-time initialization with poly-steps, poly-rate and possibly poly-noise. Therefore deep learning provides a universal learning paradigm: it was known that the approximation and estimation errors could be controlled with poly-size neural nets, using ERM that is NP-hard; this new result shows that the optimization error can also be controlled with SGD in poly-time. The picture changes for GD with large enough batches: (2) {\it Result (1) does not hold for GD:} Neural nets of poly-size trained with GD (full gradients or large enough batches) on any initialization with poly-steps, poly-range and at least poly-noise cannot learn any function distribution that has super-polynomial {\it cross-predictability,} where the cross-predictability gives a measure of ``average'' function correlation -- relations and distinctions to the statistical dimension are discussed. In particular, GD with these constraints can learn efficiently monomials of degree $k$ if and only if $k$ is constant. Thus (1) and (2) point to an interesting contrast: SGD is universal even with some poly-noise while full GD or SQ algorithms are not (e.g., parities).
Provable limitations of deep learning
Dec 16, 2018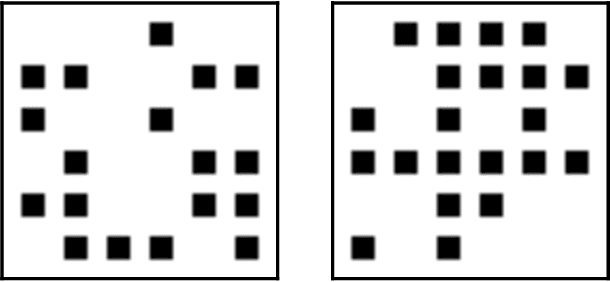
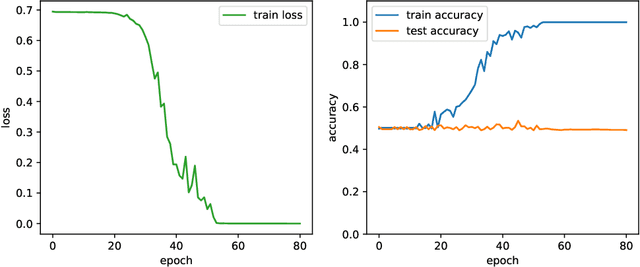
Abstract:As the success of deep learning reaches more grounds, one would like to also envision the potential limits of deep learning. This paper gives a first set of results proving that deep learning algorithms fail at learning certain efficiently learnable functions. Parity functions form the running example of our results and the paper puts forward a notion of low cross-predictability that defines a more general class of functions for which such failures tend to generalize (with examples in community detection and arithmetic learning). Recall that it is known that the class of neural networks (NNs) with polynomial network size can express any function that can be implemented in polynomial time, and that their sample complexity scales polynomially with the network size. The challenge is with the optimization error (the ERM is NP-hard), and the success behind deep learning is to train deep NNs with descent algorithms. The failures shown in this paper apply to training poly-size NNs on function distributions of low cross-predictability with a descent algorithm that is either run with limited memory per sample or that is initialized and run with enough randomness (exponentially small for GD). We further claim that such types of constraints are necessary to obtain failures, in that exact SGD with careful non-random initialization can learn parities. The cross-predictability notion has some similarity with the statistical dimension used in statistical query (SQ) algorithms, however the two definitions are different for reasons explained in the paper. The proof techniques are based on exhibiting algorithmic constraints that imply a statistical indistinguishability between the algorithm's output on the test model v.s.\ a null model, using information measures to bound the total variation distance.
Detection in the stochastic block model with multiple clusters: proof of the achievability conjectures, acyclic BP, and the information-computation gap
Sep 15, 2016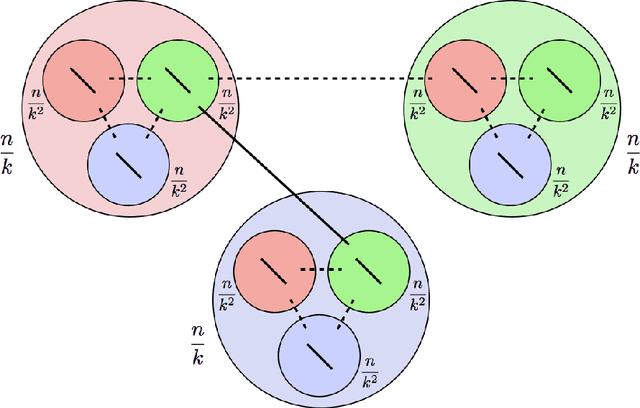
Abstract:In a paper that initiated the modern study of the stochastic block model, Decelle et al., backed by Mossel et al., made the following conjecture: Denote by $k$ the number of balanced communities, $a/n$ the probability of connecting inside communities and $b/n$ across, and set $\mathrm{SNR}=(a-b)^2/(k(a+(k-1)b)$; for any $k \geq 2$, it is possible to detect communities efficiently whenever $\mathrm{SNR}>1$ (the KS threshold), whereas for $k\geq 4$, it is possible to detect communities information-theoretically for some $\mathrm{SNR}<1$. Massouli\'e, Mossel et al.\ and Bordenave et al.\ succeeded in proving that the KS threshold is efficiently achievable for $k=2$, while Mossel et al.\ proved that it cannot be crossed information-theoretically for $k=2$. The above conjecture remained open for $k \geq 3$. This paper proves this conjecture, further extending the efficient detection to non-symmetrical SBMs with a generalized notion of detection and KS threshold. For the efficient part, a linearized acyclic belief propagation (ABP) algorithm is developed and proved to detect communities for any $k$ down to the KS threshold in time $O(n \log n)$. Achieving this requires showing optimality of ABP in the presence of cycles, a challenge for message passing algorithms. The paper further connects ABP to a power iteration method with a nonbacktracking operator of generalized order, formalizing the interplay between message passing and spectral methods. For the information-theoretic (IT) part, a non-efficient algorithm sampling a typical clustering is shown to break down the KS threshold at $k=4$. The emerging gap is shown to be large in some cases; if $a=0$, the KS threshold reads $b \gtrsim k^2$ whereas the IT bound reads $b \gtrsim k \ln(k)$, making the SBM a good study-case for information-computation gaps.
Recovering communities in the general stochastic block model without knowing the parameters
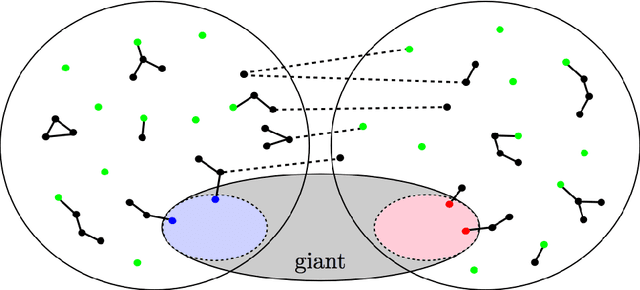
Jun 11, 2015
Abstract:Most recent developments on the stochastic block model (SBM) rely on the knowledge of the model parameters, or at least on the number of communities. This paper introduces efficient algorithms that do not require such knowledge and yet achieve the optimal information-theoretic tradeoffs identified in [AS15] for linear size communities. The results are three-fold: (i) in the constant degree regime, an algorithm is developed that requires only a lower-bound on the relative sizes of the communities and detects communities with an optimal accuracy scaling for large degrees; (ii) in the regime where degrees are scaled by $\omega(1)$ (diverging degrees), this is enhanced into a fully agnostic algorithm that only takes the graph in question and simultaneously learns the model parameters (including the number of communities) and detects communities with accuracy $1-o(1)$, with an overall quasi-linear complexity; (iii) in the logarithmic degree regime, an agnostic algorithm is developed that learns the parameters and achieves the optimal CH-limit for exact recovery, in quasi-linear time. These provide the first algorithms affording efficiency, universality and information-theoretic optimality for strong and weak consistency in the general SBM with linear size communities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge