Exploration is Harder than Prediction: Cryptographically Separating Reinforcement Learning from Supervised Learning

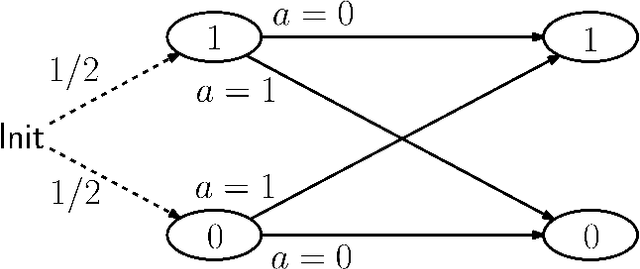
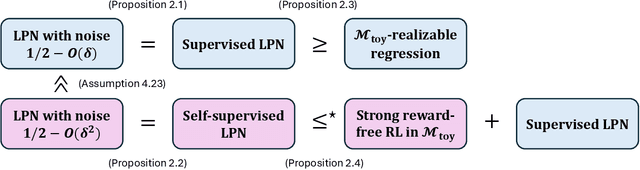
Supervised learning is often computationally easy in practice. But to what extent does this mean that other modes of learning, such as reinforcement learning (RL), ought to be computationally easy by extension? In this work we show the first cryptographic separation between RL and supervised learning, by exhibiting a class of block MDPs and associated decoding functions where reward-free exploration is provably computationally harder than the associated regression problem. We also show that there is no computationally efficient algorithm for reward-directed RL in block MDPs, even when given access to an oracle for this regression problem. It is known that being able to perform regression in block MDPs is necessary for finding a good policy; our results suggest that it is not sufficient. Our separation lower bound uses a new robustness property of the Learning Parities with Noise (LPN) hardness assumption, which is crucial in handling the dependent nature of RL data. We argue that separations and oracle lower bounds, such as ours, are a more meaningful way to prove hardness of learning because the constructions better reflect the practical reality that supervised learning by itself is often not the computational bottleneck.

Precise Error Rates for Computationally Efficient Testing

We revisit the fundamental question of simple-versus-simple hypothesis testing with an eye towards computational complexity, as the statistically optimal likelihood ratio test is often computationally intractable in high-dimensional settings. In the classical spiked Wigner model (with a general i.i.d. spike prior) we show that an existing test based on linear spectral statistics achieves the best possible tradeoff curve between type I and type II error rates among all computationally efficient tests, even though there are exponential-time tests that do better. This result is conditional on an appropriate complexity-theoretic conjecture, namely a natural strengthening of the well-established low-degree conjecture. Our result shows that the spectrum is a sufficient statistic for computationally bounded tests (but not for all tests). To our knowledge, our approach gives the first tool for reasoning about the precise asymptotic testing error achievable with efficient computation. The main ingredients required for our hardness result are a sharp bound on the norm of the low-degree likelihood ratio along with (counterintuitively) a positive result on achievability of testing. This strategy appears to be new even in the setting of unbounded computation, in which case it gives an alternate way to analyze the fundamental statistical limits of testing.

Learning quantum Hamiltonians at any temperature in polynomial time

We study the problem of learning a local quantum Hamiltonian $H$ given copies of its Gibbs state $\rho = e^{-\beta H}/\textrm{tr}(e^{-\beta H})$ at a known inverse temperature $\beta>0$. Anshu, Arunachalam, Kuwahara, and Soleimanifar (arXiv:2004.07266) gave an algorithm to learn a Hamiltonian on $n$ qubits to precision $\epsilon$ with only polynomially many copies of the Gibbs state, but which takes exponential time. Obtaining a computationally efficient algorithm has been a major open problem [Alhambra'22 (arXiv:2204.08349)], [Anshu, Arunachalam'22 (arXiv:2204.08349)], with prior work only resolving this in the limited cases of high temperature [Haah, Kothari, Tang'21 (arXiv:2108.04842)] or commuting terms [Anshu, Arunachalam, Kuwahara, Soleimanifar'21]. We fully resolve this problem, giving a polynomial time algorithm for learning $H$ to precision $\epsilon$ from polynomially many copies of the Gibbs state at any constant $\beta > 0$. Our main technical contribution is a new flat polynomial approximation to the exponential function, and a translation between multi-variate scalar polynomials and nested commutators. This enables us to formulate Hamiltonian learning as a polynomial system. We then show that solving a low-degree sum-of-squares relaxation of this polynomial system suffices to accurately learn the Hamiltonian.

Exploring and Learning in Sparse Linear MDPs without Computationally Intractable Oracles

The key assumption underlying linear Markov Decision Processes (MDPs) is that the learner has access to a known feature map $\phi(x, a)$ that maps state-action pairs to $d$-dimensional vectors, and that the rewards and transitions are linear functions in this representation. But where do these features come from? In the absence of expert domain knowledge, a tempting strategy is to use the ``kitchen sink" approach and hope that the true features are included in a much larger set of potential features. In this paper we revisit linear MDPs from the perspective of feature selection. In a $k$-sparse linear MDP, there is an unknown subset $S \subset [d]$ of size $k$ containing all the relevant features, and the goal is to learn a near-optimal policy in only poly$(k,\log d)$ interactions with the environment. Our main result is the first polynomial-time algorithm for this problem. In contrast, earlier works either made prohibitively strong assumptions that obviated the need for exploration, or required solving computationally intractable optimization problems. Along the way we introduce the notion of an emulator: a succinct approximate representation of the transitions that suffices for computing certain Bellman backups. Since linear MDPs are a non-parametric model, it is not even obvious whether polynomial-sized emulators exist. We show that they do exist and can be computed efficiently via convex programming. As a corollary of our main result, we give an algorithm for learning a near-optimal policy in block MDPs whose decoding function is a low-depth decision tree; the algorithm runs in quasi-polynomial time and takes a polynomial number of samples. This can be seen as a reinforcement learning analogue of classic results in computational learning theory. Furthermore, it gives a natural model where improving the sample complexity via representation learning is computationally feasible.

Tensor Decompositions Meet Control Theory: Learning General Mixtures of Linear Dynamical Systems

Recently Chen and Poor initiated the study of learning mixtures of linear dynamical systems. While linear dynamical systems already have wide-ranging applications in modeling time-series data, using mixture models can lead to a better fit or even a richer understanding of underlying subpopulations represented in the data. In this work we give a new approach to learning mixtures of linear dynamical systems that is based on tensor decompositions. As a result, our algorithm succeeds without strong separation conditions on the components, and can be used to compete with the Bayes optimal clustering of the trajectories. Moreover our algorithm works in the challenging partially-observed setting. Our starting point is the simple but powerful observation that the classic Ho-Kalman algorithm is a close relative of modern tensor decomposition methods for learning latent variable models. This gives us a playbook for how to extend it to work with more complicated generative models.

Provable benefits of score matching

Score matching is an alternative to maximum likelihood (ML) for estimating a probability distribution parametrized up to a constant of proportionality. By fitting the ''score'' of the distribution, it sidesteps the need to compute this constant of proportionality (which is often intractable). While score matching and variants thereof are popular in practice, precise theoretical understanding of the benefits and tradeoffs with maximum likelihood -- both computational and statistical -- are not well understood. In this work, we give the first example of a natural exponential family of distributions such that the score matching loss is computationally efficient to optimize, and has a comparable statistical efficiency to ML, while the ML loss is intractable to optimize using a gradient-based method. The family consists of exponentials of polynomials of fixed degree, and our result can be viewed as a continuous analogue of recent developments in the discrete setting. Precisely, we show: (1) Designing a zeroth-order or first-order oracle for optimizing the maximum likelihood loss is NP-hard. (2) Maximum likelihood has a statistical efficiency polynomial in the ambient dimension and the radius of the parameters of the family. (3) Minimizing the score matching loss is both computationally and statistically efficient, with complexity polynomial in the ambient dimension.

A New Approach to Learning Linear Dynamical Systems

Linear dynamical systems are the foundational statistical model upon which control theory is built. Both the celebrated Kalman filter and the linear quadratic regulator require knowledge of the system dynamics to provide analytic guarantees. Naturally, learning the dynamics of a linear dynamical system from linear measurements has been intensively studied since Rudolph Kalman's pioneering work in the 1960's. Towards these ends, we provide the first polynomial time algorithm for learning a linear dynamical system from a polynomial length trajectory up to polynomial error in the system parameters under essentially minimal assumptions: observability, controllability, and marginal stability. Our algorithm is built on a method of moments estimator to directly estimate Markov parameters from which the dynamics can be extracted. Furthermore, we provide statistical lower bounds when our observability and controllability assumptions are violated.

Minimax Rates for Robust Community Detection

In this work, we study the problem of community detection in the stochastic block model with adversarial node corruptions. Our main result is an efficient algorithm that can tolerate an $\epsilon$-fraction of corruptions and achieves error $O(\epsilon) + e^{-\frac{C}{2} (1 \pm o(1))}$ where $C = (\sqrt{a} - \sqrt{b})^2$ is the signal-to-noise ratio and $a/n$ and $b/n$ are the inter-community and intra-community connection probabilities respectively. These bounds essentially match the minimax rates for the SBM without corruptions. We also give robust algorithms for $\mathbb{Z}_2$-synchronization. At the heart of our algorithm is a new semidefinite program that uses global information to robustly boost the accuracy of a rough clustering. Moreover, we show that our algorithms are doubly-robust in the sense that they work in an even more challenging noise model that mixes adversarial corruptions with unbounded monotone changes, from the semi-random model.

Distilling Model Failures as Directions in Latent Space

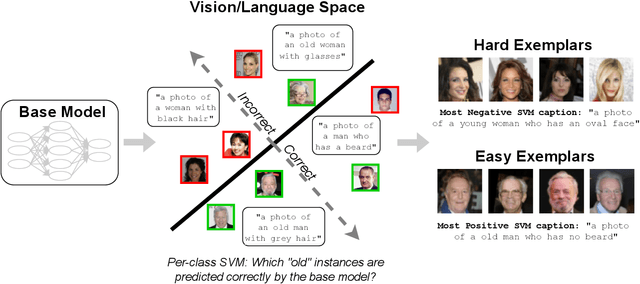
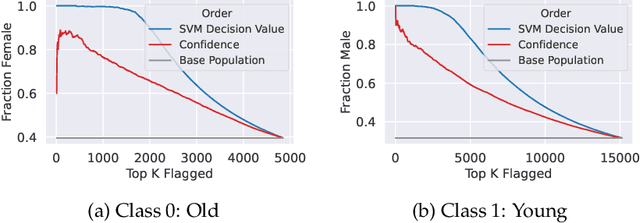
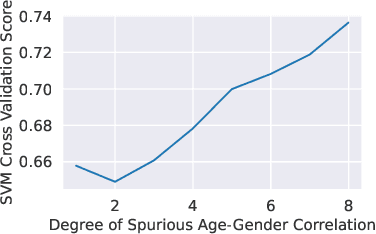
Existing methods for isolating hard subpopulations and spurious correlations in datasets often require human intervention. This can make these methods labor-intensive and dataset-specific. To address these shortcomings, we present a scalable method for automatically distilling a model's failure modes. Specifically, we harness linear classifiers to identify consistent error patterns, and, in turn, induce a natural representation of these failure modes as directions within the feature space. We demonstrate that this framework allows us to discover and automatically caption challenging subpopulations within the training dataset, and intervene to improve the model's performance on these subpopulations. Code available at https://github.com/MadryLab/failure-directions

Learning in Observable POMDPs, without Computationally Intractable Oracles

Much of reinforcement learning theory is built on top of oracles that are computationally hard to implement. Specifically for learning near-optimal policies in Partially Observable Markov Decision Processes (POMDPs), existing algorithms either need to make strong assumptions about the model dynamics (e.g. deterministic transitions) or assume access to an oracle for solving a hard optimistic planning or estimation problem as a subroutine. In this work we develop the first oracle-free learning algorithm for POMDPs under reasonable assumptions. Specifically, we give a quasipolynomial-time end-to-end algorithm for learning in "observable" POMDPs, where observability is the assumption that well-separated distributions over states induce well-separated distributions over observations. Our techniques circumvent the more traditional approach of using the principle of optimism under uncertainty to promote exploration, and instead give a novel application of barycentric spanners to constructing policy covers.