Provable benefits of score matching

Score matching is an alternative to maximum likelihood (ML) for estimating a probability distribution parametrized up to a constant of proportionality. By fitting the ''score'' of the distribution, it sidesteps the need to compute this constant of proportionality (which is often intractable). While score matching and variants thereof are popular in practice, precise theoretical understanding of the benefits and tradeoffs with maximum likelihood -- both computational and statistical -- are not well understood. In this work, we give the first example of a natural exponential family of distributions such that the score matching loss is computationally efficient to optimize, and has a comparable statistical efficiency to ML, while the ML loss is intractable to optimize using a gradient-based method. The family consists of exponentials of polynomials of fixed degree, and our result can be viewed as a continuous analogue of recent developments in the discrete setting. Precisely, we show: (1) Designing a zeroth-order or first-order oracle for optimizing the maximum likelihood loss is NP-hard. (2) Maximum likelihood has a statistical efficiency polynomial in the ambient dimension and the radius of the parameters of the family. (3) Minimizing the score matching loss is both computationally and statistically efficient, with complexity polynomial in the ambient dimension.

Progressive Knowledge Distillation: Building Ensembles for Efficient Inference

We study the problem of progressive distillation: Given a large, pre-trained teacher model $g$, we seek to decompose the model into an ensemble of smaller, low-inference cost student models $f_i$. The resulting ensemble allows for flexibly tuning accuracy vs. inference cost, which is useful for a number of applications in on-device inference. The method we propose, B-DISTIL, relies on an algorithmic procedure that uses function composition over intermediate activations to construct expressive ensembles with similar performance as $g$, but with much smaller student models. We demonstrate the effectiveness of \algA by decomposing pretrained models across standard image, speech, and sensor datasets. We also provide theoretical guarantees for our method in terms of convergence and generalization.

Pitfalls of Gaussians as a noise distribution in NCE

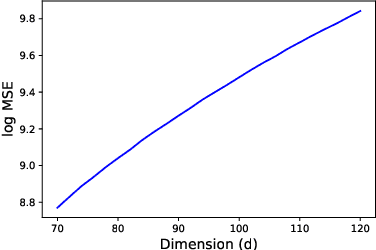
Noise Contrastive Estimation (NCE) is a popular approach for learning probability density functions parameterized up to a constant of proportionality. The main idea is to design a classification problem for distinguishing training data from samples from an easy-to-sample noise distribution $q$, in a manner that avoids having to calculate a partition function. It is well-known that the choice of $q$ can severely impact the computational and statistical efficiency of NCE. In practice, a common choice for $q$ is a Gaussian which matches the mean and covariance of the data. In this paper, we show that such a choice can result in an exponentially bad (in the ambient dimension) conditioning of the Hessian of the loss, even for very simple data distributions. As a consequence, both the statistical and algorithmic complexity for such a choice of $q$ will be problematic in practice, suggesting that more complex noise distributions are essential to the success of NCE.

Universal Approximation for Log-concave Distributions using Well-conditioned Normalizing Flows

Normalizing flows are a widely used class of latent-variable generative models with a tractable likelihood. Affine-coupling (Dinh et al, 2014-16) models are a particularly common type of normalizing flows, for which the Jacobian of the latent-to-observable-variable transformation is triangular, allowing the likelihood to be computed in linear time. Despite the widespread usage of affine couplings, the special structure of the architecture makes understanding their representational power challenging. The question of universal approximation was only recently resolved by three parallel papers (Huang et al.,2020;Zhang et al.,2020;Koehler et al.,2020) -- who showed reasonably regular distributions can be approximated arbitrarily well using affine couplings -- albeit with networks with a nearly-singular Jacobian. As ill-conditioned Jacobians are an obstacle for likelihood-based training, the fundamental question remains: which distributions can be approximated using well-conditioned affine coupling flows? In this paper, we show that any log-concave distribution can be approximated using well-conditioned affine-coupling flows. In terms of proof techniques, we uncover and leverage deep connections between affine coupling architectures, underdamped Langevin dynamics (a stochastic differential equation often used to sample from Gibbs measures) and H\'enon maps (a structured dynamical system that appears in the study of symplectic diffeomorphisms). Our results also inform the practice of training affine couplings: we approximate a padded version of the input distribution with iid Gaussians -- a strategy which Koehler et al.(2020) empirically observed to result in better-conditioned flows, but had hitherto no theoretical grounding. Our proof can thus be seen as providing theoretical evidence for the benefits of Gaussian padding when training normalizing flows.