Structure learning of Hamiltonians from real-time evolution

We initiate the study of Hamiltonian structure learning from real-time evolution: given the ability to apply $e^{-\mathrm{i} Ht}$ for an unknown local Hamiltonian $H = \sum_{a = 1}^m \lambda_a E_a$ on $n$ qubits, the goal is to recover $H$. This problem is already well-studied under the assumption that the interaction terms, $E_a$, are given, and only the interaction strengths, $\lambda_a$, are unknown. But is it possible to learn a local Hamiltonian without prior knowledge of its interaction structure? We present a new, general approach to Hamiltonian learning that not only solves the challenging structure learning variant, but also resolves other open questions in the area, all while achieving the gold standard of Heisenberg-limited scaling. In particular, our algorithm recovers the Hamiltonian to $\varepsilon$ error with an evolution time scaling with $1/\varepsilon$, and has the following appealing properties: (1) it does not need to know the Hamiltonian terms; (2) it works beyond the short-range setting, extending to any Hamiltonian $H$ where the sum of terms interacting with a qubit has bounded norm; (3) it evolves according to $H$ in constant time $t$ increments, thus achieving constant time resolution. To our knowledge, no prior algorithm with Heisenberg-limited scaling existed with even one of these properties. As an application, we can also learn Hamiltonians exhibiting power-law decay up to accuracy $\varepsilon$ with total evolution time beating the standard limit of $1/\varepsilon^2$.

Learning quantum Hamiltonians at any temperature in polynomial time

We study the problem of learning a local quantum Hamiltonian $H$ given copies of its Gibbs state $\rho = e^{-\beta H}/\textrm{tr}(e^{-\beta H})$ at a known inverse temperature $\beta>0$. Anshu, Arunachalam, Kuwahara, and Soleimanifar (arXiv:2004.07266) gave an algorithm to learn a Hamiltonian on $n$ qubits to precision $\epsilon$ with only polynomially many copies of the Gibbs state, but which takes exponential time. Obtaining a computationally efficient algorithm has been a major open problem [Alhambra'22 (arXiv:2204.08349)], [Anshu, Arunachalam'22 (arXiv:2204.08349)], with prior work only resolving this in the limited cases of high temperature [Haah, Kothari, Tang'21 (arXiv:2108.04842)] or commuting terms [Anshu, Arunachalam, Kuwahara, Soleimanifar'21]. We fully resolve this problem, giving a polynomial time algorithm for learning $H$ to precision $\epsilon$ from polynomially many copies of the Gibbs state at any constant $\beta > 0$. Our main technical contribution is a new flat polynomial approximation to the exponential function, and a translation between multi-variate scalar polynomials and nested commutators. This enables us to formulate Hamiltonian learning as a polynomial system. We then show that solving a low-degree sum-of-squares relaxation of this polynomial system suffices to accurately learn the Hamiltonian.

Do you know what q-means?

Clustering is one of the most important tools for analysis of large datasets, and perhaps the most popular clustering algorithm is Lloyd's iteration for $k$-means. This iteration takes $N$ vectors $v_1,\dots,v_N\in\mathbb{R}^d$ and outputs $k$ centroids $c_1,\dots,c_k\in\mathbb{R}^d$; these partition the vectors into clusters based on which centroid is closest to a particular vector. We present an overall improved version of the "$q$-means" algorithm, the quantum algorithm originally proposed by Kerenidis, Landman, Luongo, and Prakash (2019) which performs $\varepsilon$-$k$-means, an approximate version of $k$-means clustering. This algorithm does not rely on the quantum linear algebra primitives of prior work, instead only using its QRAM to prepare and measure simple states based on the current iteration's clusters. The time complexity is $O\big(\frac{k^{2}}{\varepsilon^2}(\sqrt{k}d + \log(Nd))\big)$ and maintains the polylogarithmic dependence on $N$ while improving the dependence on most of the other parameters. We also present a "dequantized" algorithm for $\varepsilon$-$k$-means which runs in $O\big(\frac{k^{2}}{\varepsilon^2}(kd + \log(Nd))\big)$ time. Notably, this classical algorithm matches the polylogarithmic dependence on $N$ attained by the quantum algorithms.

Optimal learning of quantum Hamiltonians from high-temperature Gibbs states

We study the problem of learning a Hamiltonian $H$ to precision $\varepsilon$, supposing we are given copies of its Gibbs state $\rho=\exp(-\beta H)/\operatorname{Tr}(\exp(-\beta H))$ at a known inverse temperature $\beta$. Anshu, Arunachalam, Kuwahara, and Soleimanifar (Nature Physics, 2021) recently studied the sample complexity (number of copies of $\rho$ needed) of this problem for geometrically local $N$-qubit Hamiltonians. In the high-temperature (low $\beta$) regime, their algorithm has sample complexity poly$(N, 1/\beta,1/\varepsilon)$ and can be implemented with polynomial, but suboptimal, time complexity. In this paper, we study the same question for a more general class of Hamiltonians. We show how to learn the coefficients of a Hamiltonian to error $\varepsilon$ with sample complexity $S = O(\log N/(\beta\varepsilon)^{2})$ and time complexity linear in the sample size, $O(S N)$. Furthermore, we prove a matching lower bound showing that our algorithm's sample complexity is optimal, and hence our time complexity is also optimal. In the appendix, we show that virtually the same algorithm can be used to learn $H$ from a real-time evolution unitary $e^{-it H}$ in a small $t$ regime with similar sample and time complexity.

Sampling-based sublinear low-rank matrix arithmetic framework for dequantizing quantum machine learning

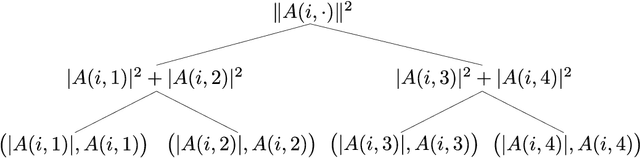
We present an algorithmic framework generalizing quantum-inspired polylogarithmic-time algorithms on low-rank matrices. Our work follows the line of research started by Tang's breakthrough classical algorithm for recommendation systems [STOC'19]. The main result of this work is an algorithm for singular value transformation on low-rank inputs in the quantum-inspired regime, where singular value transformation is a framework proposed by Gily\'en et al. [STOC'19] to study various quantum speedups. Since singular value transformation encompasses a vast range of matrix arithmetic, this result, combined with simple sampling lemmas from previous work, suffices to generalize all results dequantizing quantum machine learning algorithms to the authors' knowledge. Via simple black-box applications of our singular value transformation framework, we recover the dequantization results on recommendation systems, principal component analysis, supervised clustering, low-rank matrix inversion, low-rank semidefinite programming, and support vector machines. We also give additional dequantizations results on low-rank Hamiltonian simulation and discriminant analysis.

Quantum-inspired classical algorithms for principal component analysis and supervised clustering

We describe classical analogues to quantum algorithms for principal component analysis and nearest-centroid clustering. Given sampling assumptions, our classical algorithms run in time polylogarithmic in input, matching the runtime of the quantum algorithms with only polynomial slowdown. These algorithms are evidence that their corresponding problems do not yield exponential quantum speedups. To build our classical algorithms, we use the same techniques as applied in our previous work dequantizing a quantum recommendation systems algorithm. Thus, we provide further evidence for the strength of classical $\ell^2$-norm sampling assumptions when replacing quantum state preparation assumptions, in the machine learning domain.

A quantum-inspired classical algorithm for recommendation systems

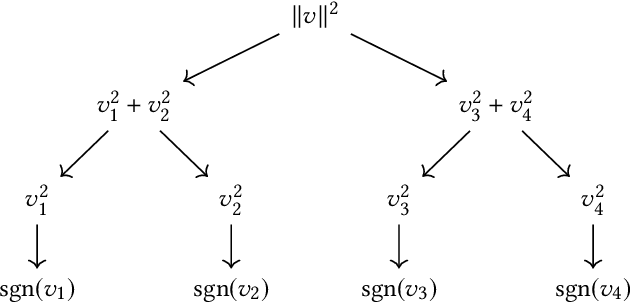
A recommendation system suggests products to users based on data about user preferences. It is typically modeled by a problem of completing an $m\times n$ matrix of small rank $k$. We give the first classical algorithm to produce a recommendation in $O(\text{poly}(k)\text{polylog}(m,n))$ time, which is an exponential improvement on previous algorithms that run in time linear in $m$ and $n$. Our strategy is inspired by a quantum algorithm by Kerenidis and Prakash: like the quantum algorithm, instead of reconstructing a user's full list of preferences, we only seek a randomized sample from the user's preferences. Our main result is an algorithm that samples high-weight entries from a low-rank approximation of the input matrix in time independent of $m$ and $n$, given natural sampling assumptions on that input matrix. As a consequence, we show that Kerenidis and Prakash's quantum machine learning (QML) algorithm, one of the strongest candidates for provably exponential speedups in QML, does not in fact give an exponential speedup over classical algorithms.