Consistency Conditions for Differentiable Surrogate Losses

The statistical consistency of surrogate losses for discrete prediction tasks is often checked via the condition of calibration. However, directly verifying calibration can be arduous. Recent work shows that for polyhedral surrogates, a less arduous condition, indirect elicitation (IE), is still equivalent to calibration. We give the first results of this type for non-polyhedral surrogates, specifically the class of convex differentiable losses. We first prove that under mild conditions, IE and calibration are equivalent for one-dimensional losses in this class. We construct a counter-example that shows that this equivalence fails in higher dimensions. This motivates the introduction of strong IE, a strengthened form of IE that is equally easy to verify. We establish that strong IE implies calibration for differentiable surrogates and is both necessary and sufficient for strongly convex, differentiable surrogates. Finally, we apply these results to a range of problems to demonstrate the power of IE and strong IE for designing and analyzing consistent differentiable surrogates.

Hedging and Approximate Truthfulness in Traditional Forecasting Competitions

In forecasting competitions, the traditional mechanism scores the predictions of each contestant against the outcome of each event, and the contestant with the highest total score wins. While it is well-known that this traditional mechanism can suffer from incentive issues, it is folklore that contestants will still be roughly truthful as the number of events grows. Yet thus far the literature lacks a formal analysis of this traditional mechanism. This paper gives the first such analysis. We first demonstrate that the ''long-run truthfulness'' folklore is false: even for arbitrary numbers of events, the best forecaster can have an incentive to hedge, reporting more moderate beliefs to increase their win probability. On the positive side, however, we show that two contestants will be approximately truthful when they have sufficient uncertainty over the relative quality of their opponent and the outcomes of the events, a case which may arise in practice.

Forecasting Competitions with Correlated Events

Beginning with Witkowski et al. [2022], recent work on forecasting competitions has addressed incentive problems with the common winner-take-all mechanism. Frongillo et al. [2021] propose a competition mechanism based on follow-the-regularized-leader (FTRL), an online learning framework. They show that their mechanism selects an $\epsilon$-optimal forecaster with high probability using only $O(\log(n)/\epsilon^2)$ events. These works, together with all prior work on this problem thus far, assume that events are independent. We initiate the study of forecasting competitions for correlated events. To quantify correlation, we introduce a notion of block correlation, which allows each event to be strongly correlated with up to $b$ others. We show that under distributions with this correlation, the FTRL mechanism retains its $\epsilon$-optimal guarantee using $O(b^2 \log(n)/\epsilon^2)$ events. Our proof involves a novel concentration bound for correlated random variables which may be of broader interest.

Consistent Polyhedral Surrogates for Top-$k$ Classification and Variants

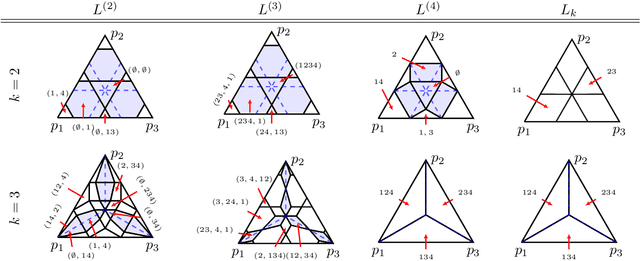
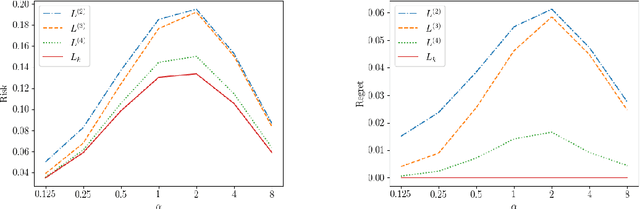
Top-$k$ classification is a generalization of multiclass classification used widely in information retrieval, image classification, and other extreme classification settings. Several hinge-like (piecewise-linear) surrogates have been proposed for the problem, yet all are either non-convex or inconsistent. For the proposed hinge-like surrogates that are convex (i.e., polyhedral), we apply the recent embedding framework of Finocchiaro et al. (2019; 2022) to determine the prediction problem for which the surrogate is consistent. These problems can all be interpreted as variants of top-$k$ classification, which may be better aligned with some applications. We leverage this analysis to derive constraints on the conditional label distributions under which these proposed surrogates become consistent for top-$k$. It has been further suggested that every convex hinge-like surrogate must be inconsistent for top-$k$. Yet, we use the same embedding framework to give the first consistent polyhedral surrogate for this problem.

Efficient Competitions and Online Learning with Strategic Forecasters

Winner-take-all competitions in forecasting and machine-learning suffer from distorted incentives. Witkowskiet al. identified this problem and proposed ELF, a truthful mechanism to select a winner. We show that, from a pool of $n$ forecasters, ELF requires $\Theta(n\log n)$ events or test data points to select a near-optimal forecaster with high probability. We then show that standard online learning algorithms select an $\epsilon$-optimal forecaster using only $O(\log(n) / \epsilon^2)$ events, by way of a strong approximate-truthfulness guarantee. This bound matches the best possible even in the nonstrategic setting. We then apply these mechanisms to obtain the first no-regret guarantee for non-myopic strategic experts.