Evolutionary Multi-Objective Diversity Optimization

Creating diverse sets of high quality solutions has become an important problem in recent years. Previous works on diverse solutions problems consider solutions' objective quality and diversity where one is regarded as the optimization goal and the other as the constraint. In this paper, we treat this problem as a bi-objective optimization problem, which is to obtain a range of quality-diversity trade-offs. To address this problem, we frame the evolutionary process as evolving a population of populations, and present a suitable general implementation scheme that is compatible with existing evolutionary multi-objective search methods. We realize the scheme in NSGA-II and SPEA2, and test the methods on various instances of maximum coverage, maximum cut and minimum vertex cover problems. The resulting non-dominated populations exhibit rich qualitative features, giving insights into the optimization instances and the quality-diversity trade-offs they induce.

Optimizing Chance-Constrained Submodular Problems with Variable Uncertainties

Chance constraints are frequently used to limit the probability of constraint violations in real-world optimization problems where the constraints involve stochastic components. We study chance-constrained submodular optimization problems, which capture a wide range of optimization problems with stochastic constraints. Previous studies considered submodular problems with stochastic knapsack constraints in the case where uncertainties are the same for each item that can be selected. However, uncertainty levels are usually variable with respect to the different stochastic components in real-world scenarios, and rigorous analysis for this setting is missing in the context of submodular optimization. This paper provides the first such analysis for this case, where the weights of items have the same expectation but different dispersion. We present greedy algorithms that can obtain a high-quality solution, i.e., a constant approximation ratio to the given optimal solution from the deterministic setting. In the experiments, we demonstrate that the algorithms perform effectively on several chance-constrained instances of the maximum coverage problem and the influence maximization problem.

Rigorous Runtime Analysis of MOEA/D for Solving Multi-Objective Minimum Weight Base Problems

We study the multi-objective minimum weight base problem, an abstraction of classical NP-hard combinatorial problems such as the multi-objective minimum spanning tree problem. We prove some important properties of the convex hull of the non-dominated front, such as its approximation quality and an upper bound on the number of extreme points. Using these properties, we give the first run-time analysis of the MOEA/D algorithm for this problem, an evolutionary algorithm that effectively optimizes by decomposing the objectives into single-objective components. We show that the MOEA/D, given an appropriate decomposition setting, finds all extreme points within expected fixed-parameter polynomial time in the oracle model, the parameter being the number of objectives. Experiments are conducted on random bi-objective minimum spanning tree instances, and the results agree with our theoretical findings. Furthermore, compared with a previously studied evolutionary algorithm for the problem GSEMO, MOEA/D finds all extreme points much faster across all instances.

Analysis of Quality Diversity Algorithms for the Knapsack Problem

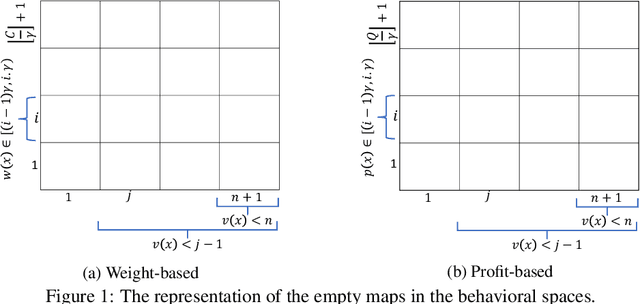
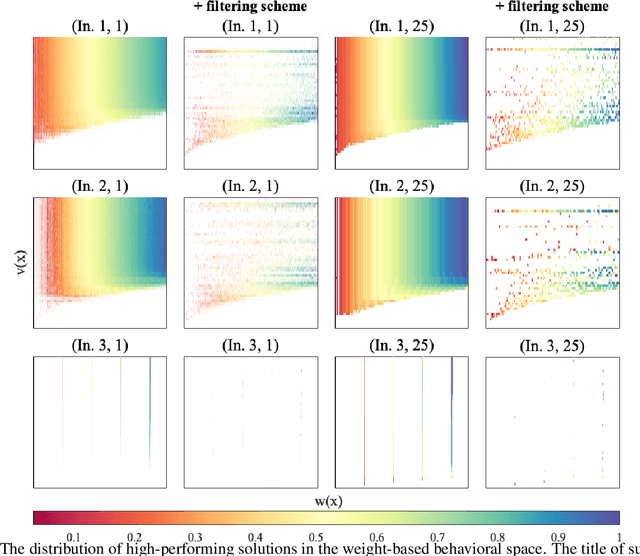
Quality diversity (QD) algorithms have been shown to be very successful when dealing with problems in areas such as robotics, games and combinatorial optimization. They aim to maximize the quality of solutions for different regions of the so-called behavioural space of the underlying problem. In this paper, we apply the QD paradigm to simulate dynamic programming behaviours on knapsack problem, and provide a first runtime analysis of QD algorithms. We show that they are able to compute an optimal solution within expected pseudo-polynomial time, and reveal parameter settings that lead to a fully polynomial randomised approximation scheme (FPRAS). Our experimental investigations evaluate the different approaches on classical benchmark sets in terms of solutions constructed in the behavioural space as well as the runtime needed to obtain an optimal solution.

Niching-based Evolutionary Diversity Optimization for the Traveling Salesperson Problem

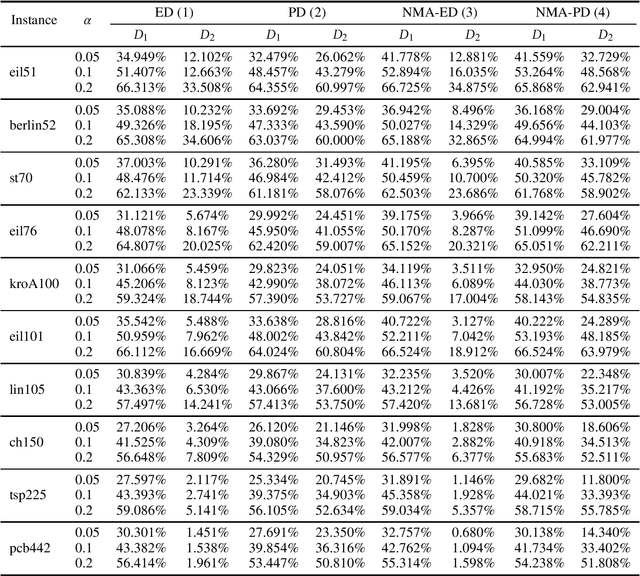
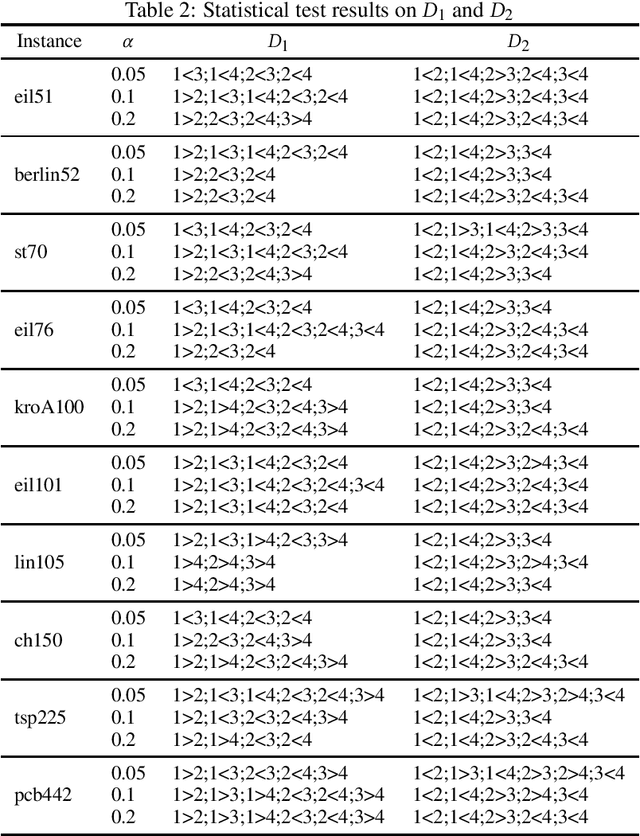
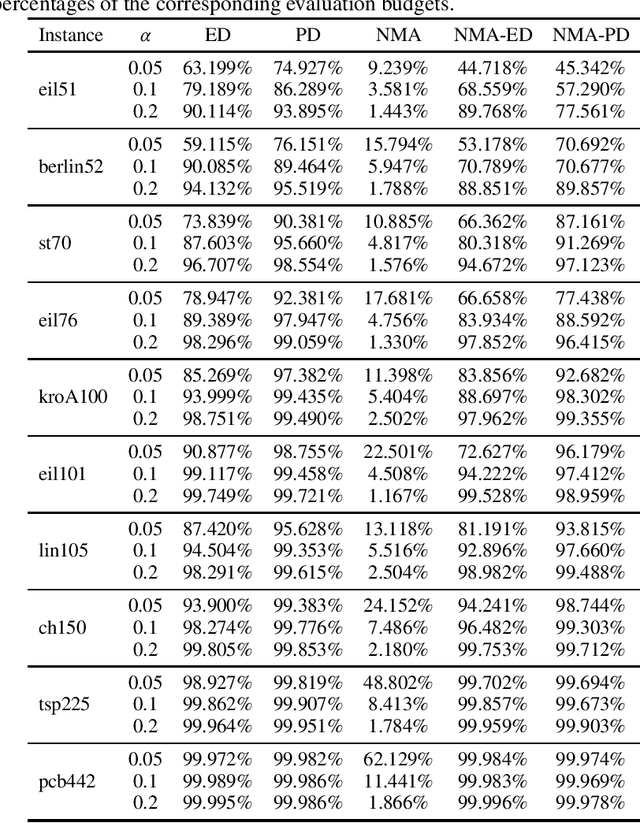
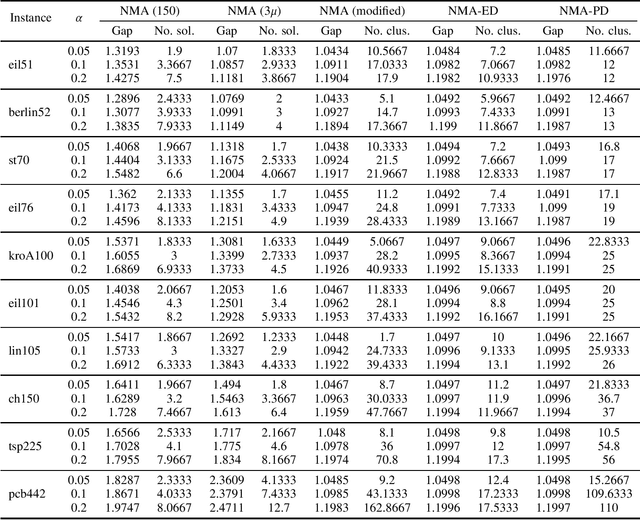
In this work, we consider the problem of finding a set of tours to a traveling salesperson problem (TSP) instance maximizing diversity, while satisfying a given cost constraint. This study aims to investigate the effectiveness of applying niching to maximize diversity rather than simply maintaining it. To this end, we introduce a 2-stage approach where a simple niching memetic algorithm (NMA), derived from a state-of-the-art for multi-solution TSP, is combined with a baseline diversifying algorithm. The most notable feature of the proposed NMA is the use of randomized improvement-first local search instead of 2-opt. Our experiment on TSPLIB instances shows that while the populations evolved by our NMA tend to contain clusters at tight quality constraints, they frequently occupy distant basins of attraction rather than close-by regions, improving on the baseline diversification in terms of sum-sum diversity. Compared to the original NMA, ours, despite its simplicity, finds more distant solutions of higher quality within less running time, by a large margin.

Analysis of Evolutionary Diversity Optimisation for Permutation Problems

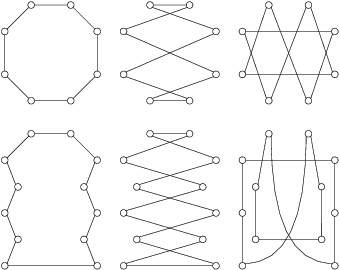
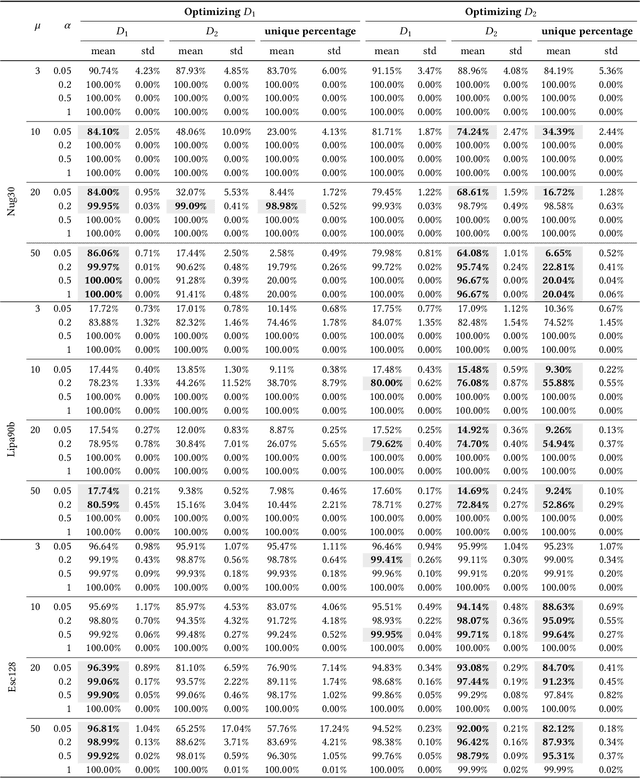
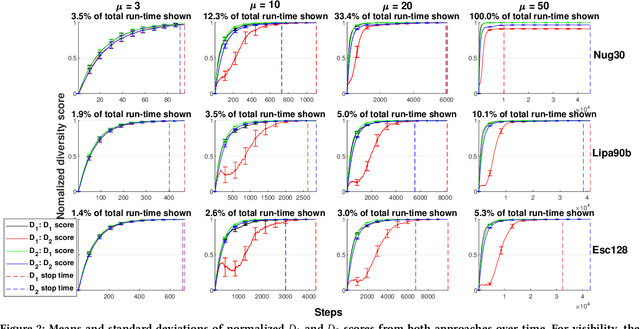
Generating diverse populations of high quality solutions has gained interest as a promising extension to the traditional optimization tasks. We contribute to this line of research by studying evolutionary diversity optimization for two of the most prominent permutation problems, namely the Traveling Salesperson Problem (TSP) and Quadratic Assignment Problem (QAP). We explore the worst-case performance of a simple mutation-only evolutionary algorithm with different mutation operators, using an established diversity measure. Theoretical results show most mutation operators for both problems ensure production of maximally diverse populations of sufficiently small size within cubic expected run-time. We perform experiments on QAPLIB instances in unconstrained and constrained settings, and reveal much more optimistic practical performances. Our results should serve as a baseline for future studies.

Pareto Optimization for Subset Selection with Dynamic Partition Matroid Constraints

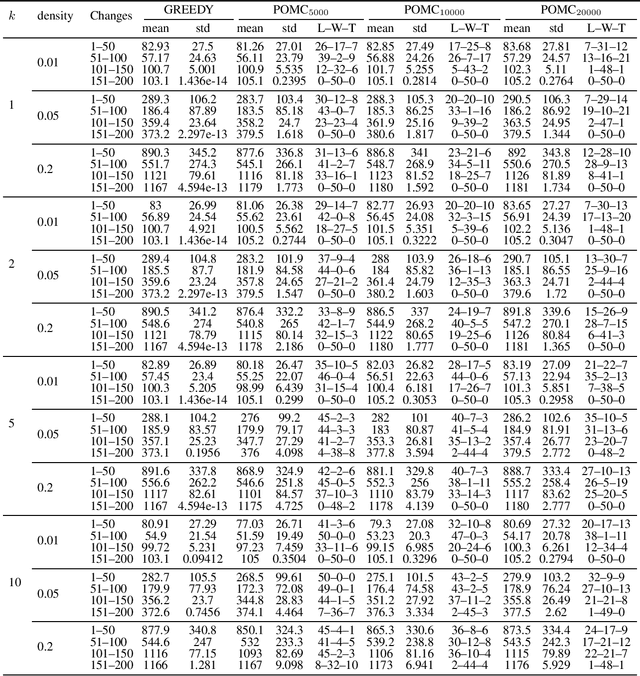
In this study, we consider the subset selection problems with submodular or monotone discrete objective functions under partition matroid constraints where the thresholds are dynamic. We focus on POMC, a simple Pareto optimization approach that has been shown to be effective on such problems. Our analysis departs from singular constraint problems and extends to problems of multiple constraints. We show that previous results of POMC's performance also hold for multiple constraints. Our experimental investigations on random undirected maxcut problems demonstrate POMC's competitiveness against the classical GREEDY algorithm with restart strategy.

Maximizing Submodular or Monotone Functions under Partition Matroid Constraints by Multi-objective Evolutionary Algorithms

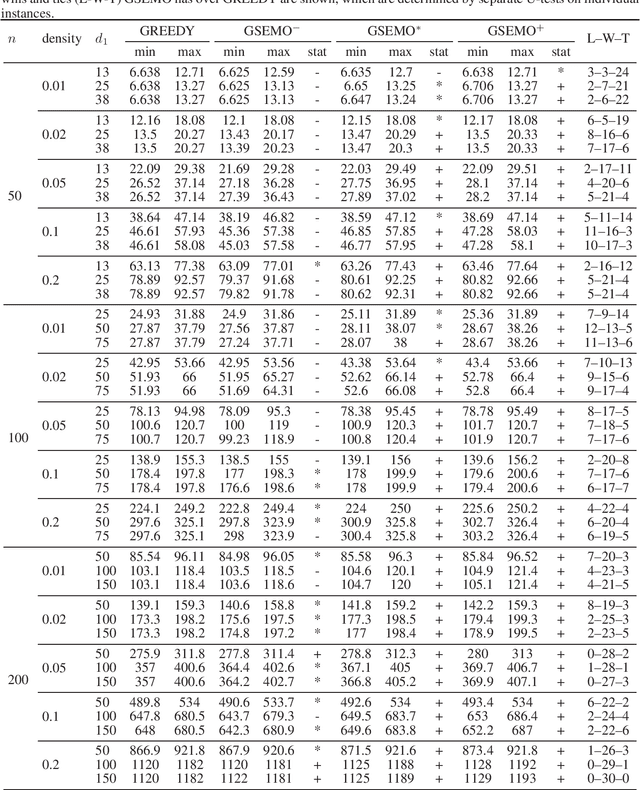
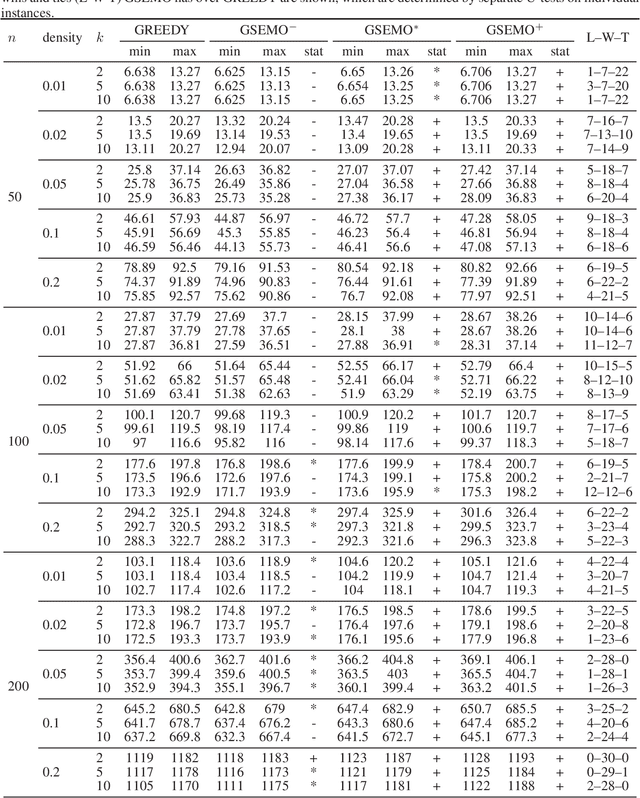
Many important problems can be regarded as maximizing submodular functions under some constraints. A simple multi-objective evolutionary algorithm called GSEMO has been shown to achieve good approximation for submodular functions efficiently. While there have been many studies on the subject, most of existing run-time analyses for GSEMO assume a single cardinality constraint. In this work, we extend the theoretical results to partition matroid constraints which generalize cardinality constraints, and show that GSEMO can generally guarantee good approximation performance within polynomial expected run time. Furthermore, we conducted experimental comparison against a baseline GREEDY algorithm in maximizing undirected graph cuts on random graphs, under various partition matroid constraints. The results show GSEMO tends to outperform GREEDY in quadratic run time.

Evolving Diverse Sets of Tours for the Travelling Salesperson Problem

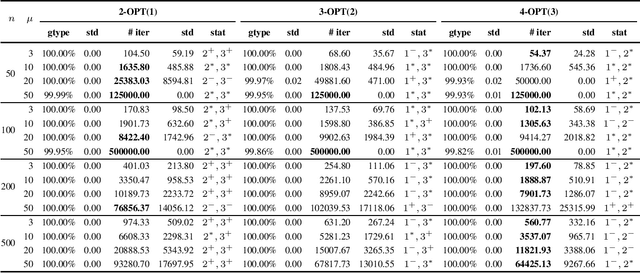
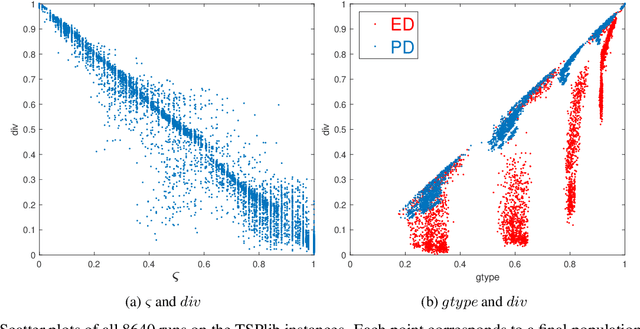
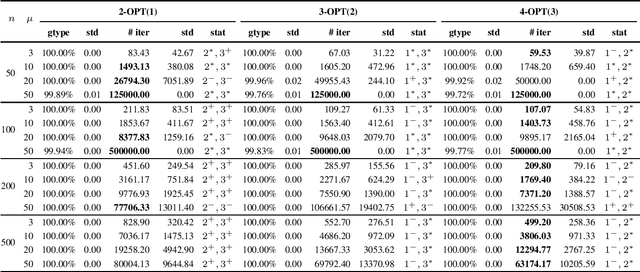
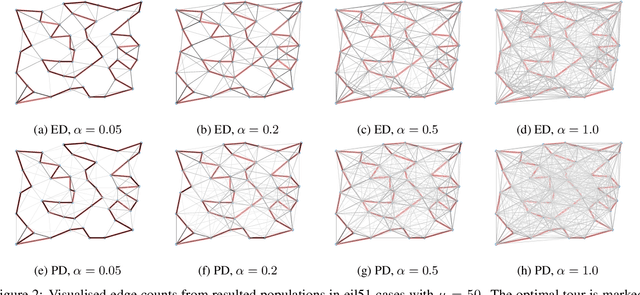
Evolving diverse sets of high quality solutions has gained increasing interest in the evolutionary computation literature in recent years. With this paper, we contribute to this area of research by examining evolutionary diversity optimisation approaches for the classical Traveling Salesperson Problem (TSP). We study the impact of using different diversity measures for a given set of tours and the ability of evolutionary algorithms to obtain a diverse set of high quality solutions when adopting these measures. Our studies show that a large variety of diverse high quality tours can be achieved by using our approaches. Furthermore, we compare our approaches in terms of theoretical properties and the final set of tours obtained by the evolutionary diversity optimisation algorithm.