On Single-Objective Sub-Graph-Based Mutation for Solving the Bi-Objective Minimum Spanning Tree Problem

We contribute to the efficient approximation of the Pareto-set for the classical $\mathcal{NP}$-hard multi-objective minimum spanning tree problem (moMST) adopting evolutionary computation. More precisely, by building upon preliminary work, we analyse the neighborhood structure of Pareto-optimal spanning trees and design several highly biased sub-graph-based mutation operators founded on the gained insights. In a nutshell, these operators replace (un)connected sub-trees of candidate solutions with locally optimal sub-trees. The latter (biased) step is realized by applying Kruskal's single-objective MST algorithm to a weighted sum scalarization of a sub-graph. We prove runtime complexity results for the introduced operators and investigate the desirable Pareto-beneficial property. This property states that mutants cannot be dominated by their parent. Moreover, we perform an extensive experimental benchmark study to showcase the operator's practical suitability. Our results confirm that the sub-graph based operators beat baseline algorithms from the literature even with severely restricted computational budget in terms of function evaluations on four different classes of complete graphs with different shapes of the Pareto-front.

Runtime Analysis of Quality Diversity Algorithms

Quality diversity~(QD) is a branch of evolutionary computation that gained increasing interest in recent years. The Map-Elites QD approach defines a feature space, i.e., a partition of the search space, and stores the best solution for each cell of this space. We study a simple QD algorithm in the context of pseudo-Boolean optimisation on the ``number of ones'' feature space, where the $i$th cell stores the best solution amongst those with a number of ones in $[(i-1)k, ik-1]$. Here $k$ is a granularity parameter $1 \leq k \leq n+1$. We give a tight bound on the expected time until all cells are covered for arbitrary fitness functions and for all $k$ and analyse the expected optimisation time of QD on \textsc{OneMax} and other problems whose structure aligns favourably with the feature space. On combinatorial problems we show that QD finds a ${(1-1/e)}$-approximation when maximising any monotone sub-modular function with a single uniform cardinality constraint efficiently. Defining the feature space as the number of connected components of a connected graph, we show that QD finds a minimum spanning tree in expected polynomial time.

On the Impact of Operators and Populations within Evolutionary Algorithms for the Dynamic Weighted Traveling Salesperson Problem

Evolutionary algorithms have been shown to obtain good solutions for complex optimization problems in static and dynamic environments. It is important to understand the behaviour of evolutionary algorithms for complex optimization problems that also involve dynamic and/or stochastic components in a systematic way in order to further increase their applicability to real-world problems. We investigate the node weighted traveling salesperson problem (W-TSP), which provides an abstraction of a wide range of weighted TSP problems, in dynamic settings. In the dynamic setting of the problem, items that have to be collected as part of a TSP tour change over time. We first present a dynamic setup for the dynamic W-TSP parameterized by different types of changes that are applied to the set of items to be collected when traversing the tour. Our first experimental investigations study the impact of such changes on resulting optimized tours in order to provide structural insights of optimization solutions. Afterwards, we investigate simple mutation-based evolutionary algorithms and study the impact of the mutation operators and the use of populations with dealing with the dynamic changes to the node weights of the problem.

Co-Evolutionary Diversity Optimisation for the Traveling Thief Problem

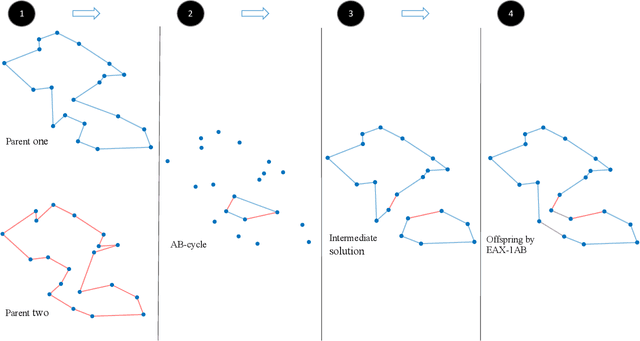
Recently different evolutionary computation approaches have been developed that generate sets of high quality diverse solutions for a given optimisation problem. Many studies have considered diversity 1) as a mean to explore niches in behavioural space (quality diversity) or 2) to increase the structural differences of solutions (evolutionary diversity optimisation). In this study, we introduce a co-evolutionary algorithm to simultaneously explore the two spaces for the multi-component traveling thief problem. The results show the capability of the co-evolutionary algorithm to achieve significantly higher diversity compared to the baseline evolutionary diversity algorithms from the the literature.

Exploring the Feature Space of TSP Instances Using Quality Diversity

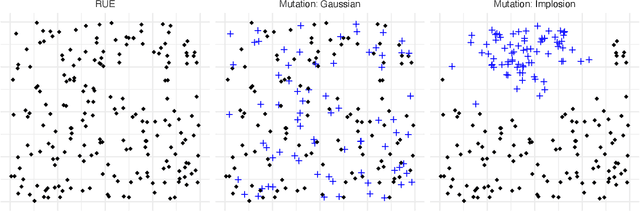
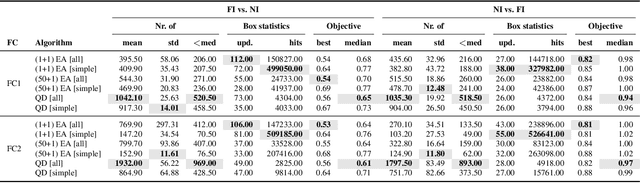
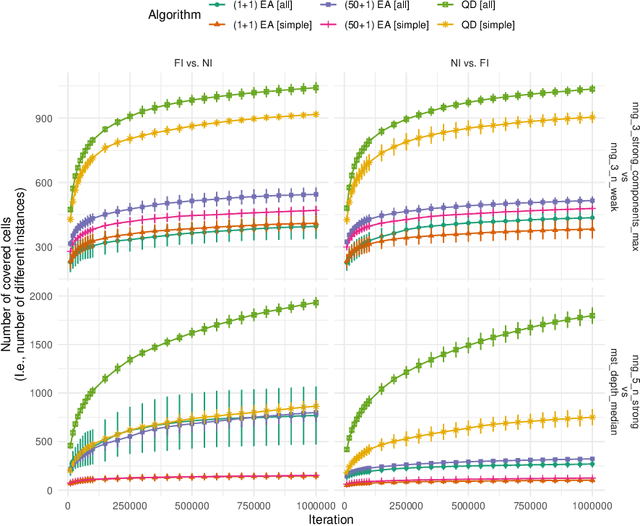
Generating instances of different properties is key to algorithm selection methods that differentiate between the performance of different solvers for a given combinatorial optimization problem. A wide range of methods using evolutionary computation techniques has been introduced in recent years. With this paper, we contribute to this area of research by providing a new approach based on quality diversity (QD) that is able to explore the whole feature space. QD algorithms allow to create solutions of high quality within a given feature space by splitting it up into boxes and improving solution quality within each box. We use our QD approach for the generation of TSP instances to visualize and analyze the variety of instances differentiating various TSP solvers and compare it to instances generated by a $(\mu+1)$-EA for TSP instance generation.

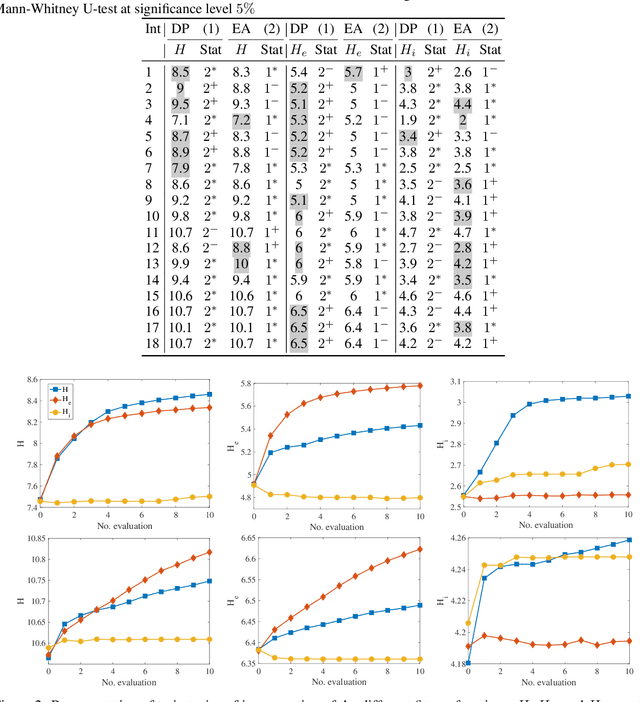
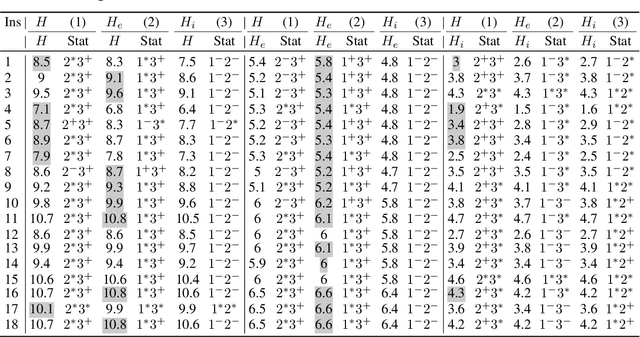
Computing Diverse Sets of High Quality TSP Tours by EAX-Based Evolutionary Diversity Optimisation

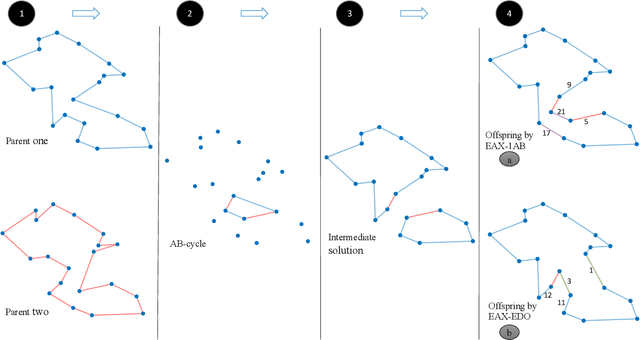
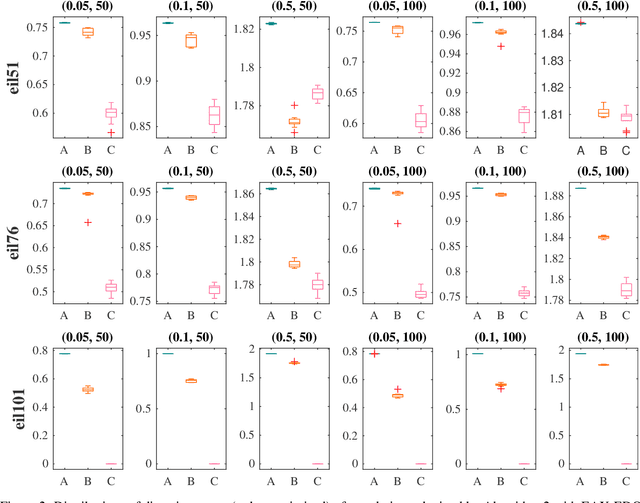
Evolutionary algorithms based on edge assembly crossover (EAX) constitute some of the best performing incomplete solvers for the well-known traveling salesperson problem (TSP). Often, it is desirable to compute not just a single solution for a given problem, but a diverse set of high quality solutions from which a decision maker can choose one for implementation. Currently, there are only a few approaches for computing a diverse solution set for the TSP. Furthermore, almost all of them assume that the optimal solution is known. In this paper, we introduce evolutionary diversity optimisation (EDO) approaches for the TSP that find a diverse set of tours when the optimal tour is known or unknown. We show how to adopt EAX to not only find a high-quality solution but also to maximise the diversity of the population. The resulting EAX-based EDO approach, termed EAX-EDO is capable of obtaining diverse high-quality tours when the optimal solution for the TSP is known or unknown. A comparison to existing approaches shows that they are clearly outperformed by EAX-EDO.

Time Complexity Analysis of Randomized Search Heuristics for the Dynamic Graph Coloring Problem

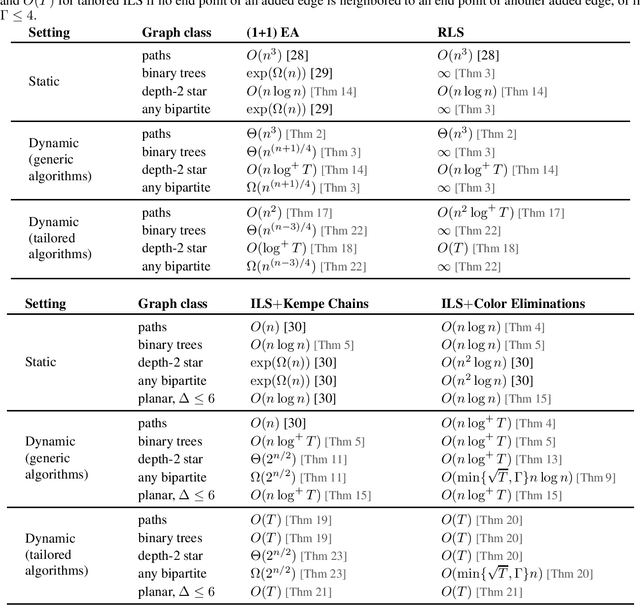
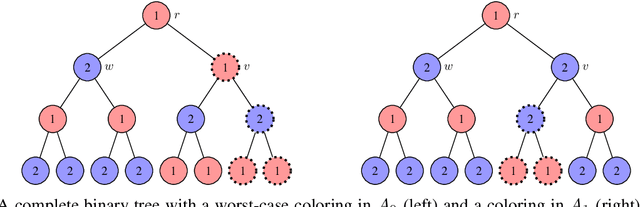
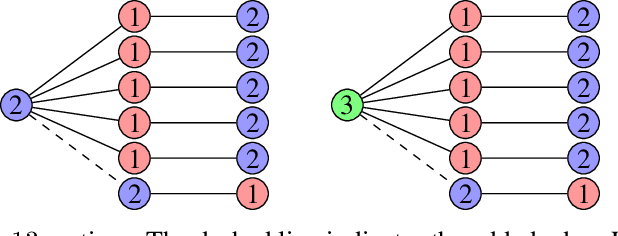
We contribute to the theoretical understanding of randomized search heuristics for dynamic problems. We consider the classical vertex coloring problem on graphs and investigate the dynamic setting where edges are added to the current graph. We then analyze the expected time for randomized search heuristics to recompute high quality solutions. The (1+1)~Evolutionary Algorithm and RLS operate in a setting where the number of colors is bounded and we are minimizing the number of conflicts. Iterated local search algorithms use an unbounded color palette and aim to use the smallest colors and, consequently, the smallest number of colors. We identify classes of bipartite graphs where reoptimization is as hard as or even harder than optimization from scratch, i.e., starting with a random initialization. Even adding a single edge can lead to hard symmetry problems. However, graph classes that are hard for one algorithm turn out to be easy for others. In most cases our bounds show that reoptimization is faster than optimizing from scratch. We further show that tailoring mutation operators to parts of the graph where changes have occurred can significantly reduce the expected reoptimization time. In most settings the expected reoptimization time for such tailored algorithms is linear in the number of added edges. However, tailored algorithms cannot prevent exponential times in settings where the original algorithm is inefficient.

Generating Instances with Performance Differences for More Than Just Two Algorithms

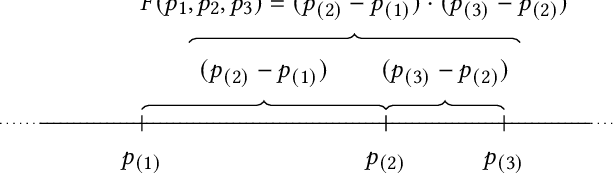
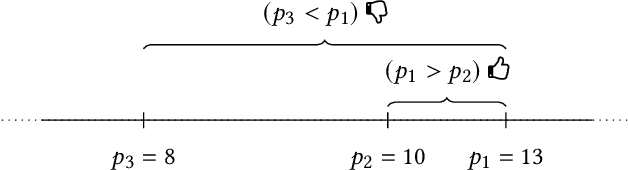
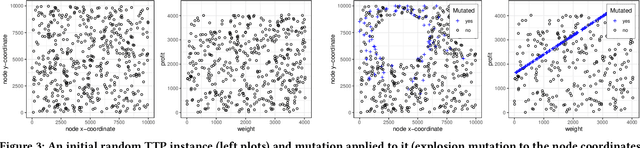
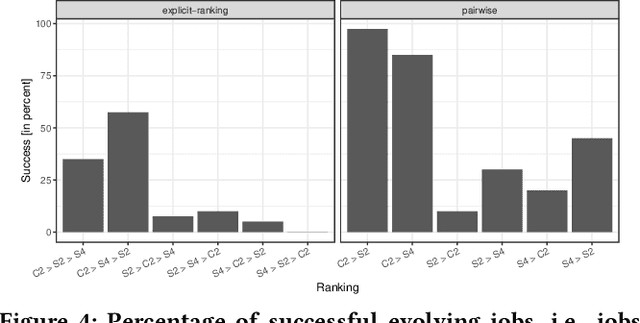
In recent years, Evolutionary Algorithms (EAs) have frequently been adopted to evolve instances for optimization problems that pose difficulties for one algorithm while being rather easy for a competitor and vice versa. Typically, this is achieved by either minimizing or maximizing the performance difference or ratio which serves as the fitness function. Repeating this process is useful to gain insights into strengths/weaknesses of certain algorithms or to build a set of instances with strong performance differences as a foundation for automatic per-instance algorithm selection or configuration. We contribute to this branch of research by proposing fitness-functions to evolve instances that show large performance differences for more than just two algorithms simultaneously. As a proof-of-principle, we evolve instances of the multi-component Traveling Thief Problem~(TTP) for three incomplete TTP-solvers. Our results point out that our strategies are promising, but unsurprisingly their success strongly relies on the algorithms' performance complementarity.

Entropy-Based Evolutionary Diversity Optimisation for the Traveling Salesperson Problem

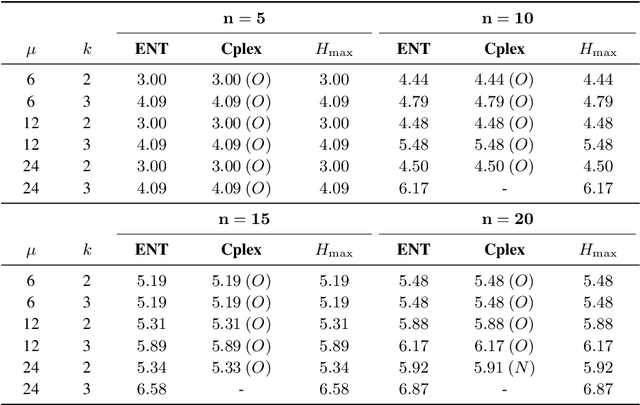
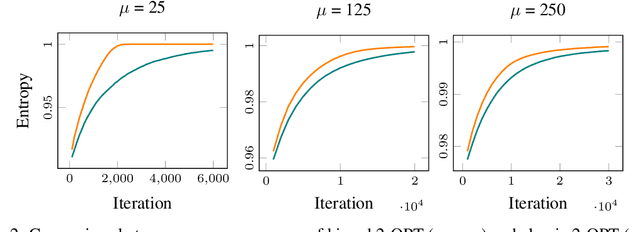
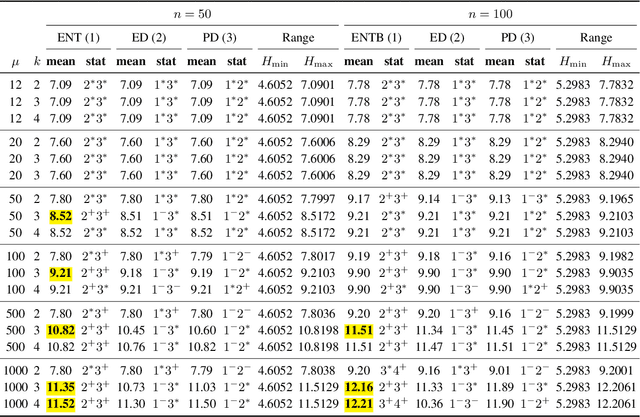
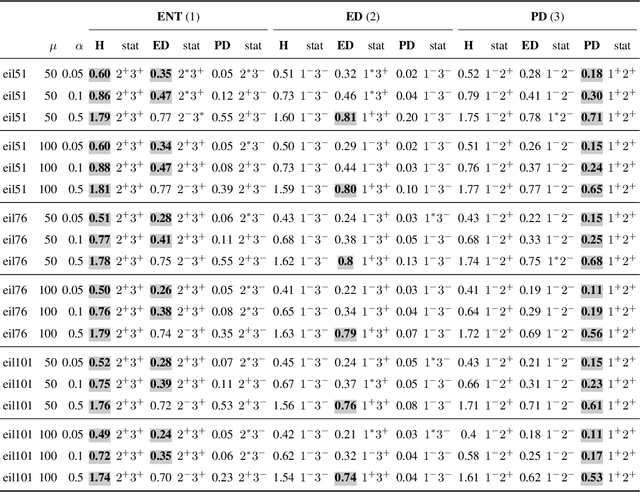
Computing diverse sets of high-quality solutions has gained increasing attention among the evolutionary computation community in recent years. It allows practitioners to choose from a set of high-quality alternatives. In this paper, we employ a population diversity measure, called the high-order entropy measure, in an evolutionary algorithm to compute a diverse set of high-quality solutions for the Traveling Salesperson Problem. In contrast to previous studies, our approach allows diversifying segments of tours containing several edges based on the entropy measure. We examine the resulting evolutionary diversity optimisation approach precisely in terms of the final set of solutions and theoretical properties. Experimental results show significant improvements compared to a recently proposed edge-based diversity optimisation approach when working with a large population of solutions or long segments.

Breeding Diverse Packings for the Knapsack Problem by Means of Diversity-Tailored Evolutionary Algorithms

In practise, it is often desirable to provide the decision-maker with a rich set of diverse solutions of decent quality instead of just a single solution. In this paper we study evolutionary diversity optimization for the knapsack problem (KP). Our goal is to evolve a population of solutions that all have a profit of at least $(1-\varepsilon)\cdot OPT$, where OPT is the value of an optimal solution. Furthermore, they should differ in structure with respect to an entropy-based diversity measure. To this end we propose a simple $(\mu+1)$-EA with initial approximate solutions calculated by a well-known FPTAS for the KP. We investigate the effect of different standard mutation operators and introduce biased mutation and crossover which puts strong probability on flipping bits of low and/or high frequency within the population. An experimental study on different instances and settings shows that the proposed mutation operators in most cases perform slightly inferior in the long term, but show strong benefits if the number of function evaluations is severely limited.