Fixed-Parameter Tractability of the (1+1) Evolutionary Algorithm on Random Planted Vertex Covers

We present the first parameterized analysis of a standard (1+1) Evolutionary Algorithm on a distribution of vertex cover problems. We show that if the planted cover is at most logarithmic, restarting the (1+1) EA every $O(n \log n)$ steps will find a cover at least as small as the planted cover in polynomial time for sufficiently dense random graphs $p > 0.71$. For superlogarithmic planted covers, we prove that the (1+1) EA finds a solution in fixed-parameter tractable time in expectation. We complement these theoretical investigations with a number of computational experiments that highlight the interplay between planted cover size, graph density and runtime.

Runtime Analysis of Evolutionary Diversity Optimization on the Multi-objective (LeadingOnes, TrailingZeros) Problem

The diversity optimization is the class of optimization problems, in which we aim at finding a diverse set of good solutions. One of the frequently used approaches to solve such problems is to use evolutionary algorithms which evolve a desired diverse population. This approach is called evolutionary diversity optimization (EDO). In this paper, we analyse EDO on a 3-objective function LOTZ$_k$, which is a modification of the 2-objective benchmark function (LeadingOnes, TrailingZeros). We prove that the GSEMO computes a set of all Pareto-optimal solutions in $O(kn^3)$ expected iterations. We also analyze the runtime of the GSEMO$_D$ (a modification of the GSEMO for diversity optimization) until it finds a population with the best possible diversity for two different diversity measures, the total imbalance and the sorted imbalances vector. For the first measure we show that the GSEMO$_D$ optimizes it asymptotically faster than it finds a Pareto-optimal population, in $O(kn^2\log(n))$ expected iterations, and for the second measure we show an upper bound of $O(k^2n^3\log(n))$ expected iterations. We complement our theoretical analysis with an empirical study, which shows a very similar behavior for both diversity measures that is close to the theory predictions.

Rigorous Runtime Analysis of MOEA/D for Solving Multi-Objective Minimum Weight Base Problems

We study the multi-objective minimum weight base problem, an abstraction of classical NP-hard combinatorial problems such as the multi-objective minimum spanning tree problem. We prove some important properties of the convex hull of the non-dominated front, such as its approximation quality and an upper bound on the number of extreme points. Using these properties, we give the first run-time analysis of the MOEA/D algorithm for this problem, an evolutionary algorithm that effectively optimizes by decomposing the objectives into single-objective components. We show that the MOEA/D, given an appropriate decomposition setting, finds all extreme points within expected fixed-parameter polynomial time in the oracle model, the parameter being the number of objectives. Experiments are conducted on random bi-objective minimum spanning tree instances, and the results agree with our theoretical findings. Furthermore, compared with a previously studied evolutionary algorithm for the problem GSEMO, MOEA/D finds all extreme points much faster across all instances.

Focused Jump-and-Repair Constraint Handling for Fixed-Parameter Tractable Graph Problems

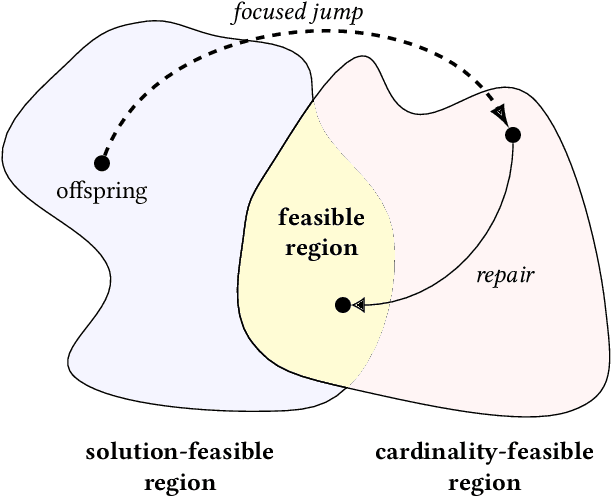
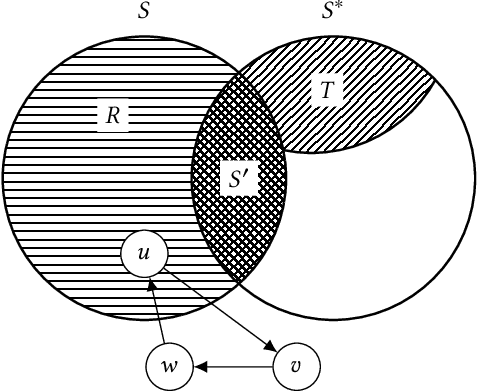
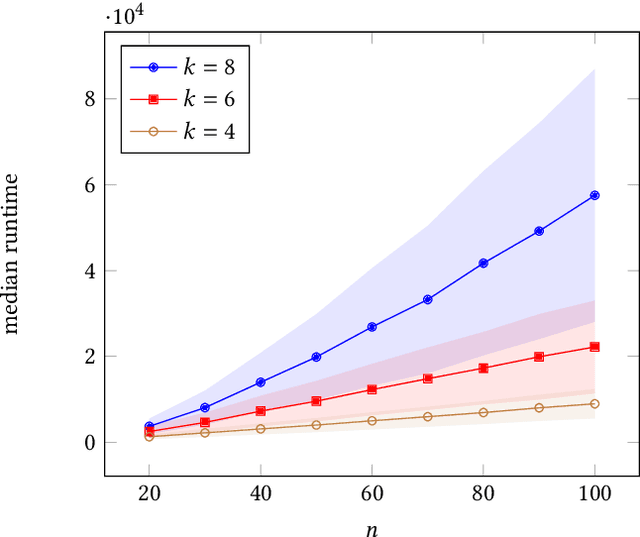
Repair operators are often used for constraint handling in constrained combinatorial optimization. We investigate the (1+1) EA equipped with a tailored jump-and-repair operation that can be used to probabilistically repair infeasible offspring in graph problems. Instead of evolving candidate solutions to the entire graph, we expand the genotype to allow the (1+1) EA to develop in parallel a feasible solution together with a growing subset of the instance (an induced subgraph). With this approach, we prove that the EA is able to probabilistically simulate an iterative compression process used in classical fixed-parameter algorithmics to obtain a randomized FPT performance guarantee on three NP-hard graph problems. For $k$-VertexCover, we prove that the (1+1) EA using focused jump-and-repair can find a $k$-cover (if one exists) in $O(2^k n^2\log n)$ iterations in expectation. This leads to an exponential (in $k$) improvement over the best-known parameterized bound for evolutionary algorithms on VertexCover. For the $k$-FeedbackVertexSet problem in tournaments, we prove that the EA finds a feasible feedback set in $O(2^kk!n^2\log n)$ iterations in expectation, and for OddCycleTransversal, we prove the optimization time for the EA is $O(3^k k m n^2\log n)$. For the latter two problems, this constitutes the first parameterized result for any evolutionary algorithm. We discuss how to generalize the framework to other parameterized graph problems closed under induced subgraphs and report experimental results that illustrate the behavior of the algorithm on a concrete instance class.

Runtime Analysis of RLS and the EA for the Chance-constrained Knapsack Problem with Correlated Uniform Weights

Addressing a complex real-world optimization problem is a challenging task. The chance-constrained knapsack problem with correlated uniform weights plays an important role in the case where dependent stochastic components are considered. We perform runtime analysis of a randomized search algorithm (RSA) and a basic evolutionary algorithm (EA) for the chance-constrained knapsack problem with correlated uniform weights. We prove bounds for both algorithms for producing a feasible solution. Furthermore, we investigate the behavior of the algorithms and carry out analyses on two settings: uniform profit value and the setting in which every group shares an arbitrary profit profile. We provide insight into the structure of these problems and show how the weight correlations and the different types of profit profiles influence the runtime behavior of both algorithms in the chance-constrained setting.

Parameterized Complexity Analysis of Randomized Search Heuristics

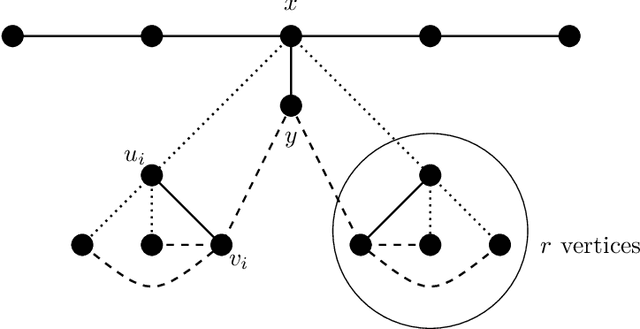
This chapter compiles a number of results that apply the theory of parameterized algorithmics to the running-time analysis of randomized search heuristics such as evolutionary algorithms. The parameterized approach articulates the running time of algorithms solving combinatorial problems in finer detail than traditional approaches from classical complexity theory. We outline the main results and proof techniques for a collection of randomized search heuristics tasked to solve NP-hard combinatorial optimization problems such as finding a minimum vertex cover in a graph, finding a maximum leaf spanning tree in a graph, and the traveling salesperson problem.

Optimization of Chance-Constrained Submodular Functions

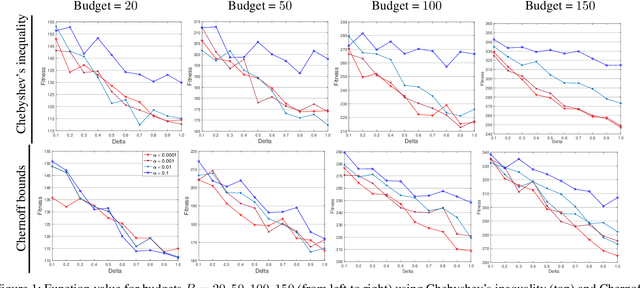
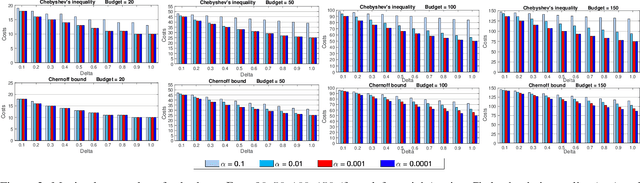
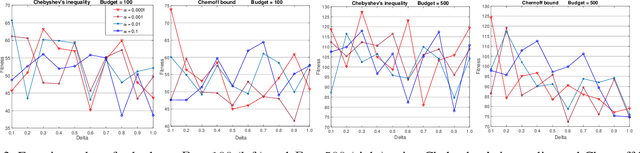
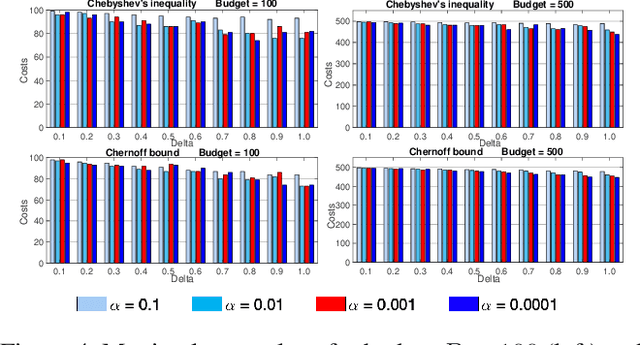
Submodular optimization plays a key role in many real-world problems. In many real-world scenarios, it is also necessary to handle uncertainty, and potentially disruptive events that violate constraints in stochastic settings need to be avoided. In this paper, we investigate submodular optimization problems with chance constraints. We provide a first analysis on the approximation behavior of popular greedy algorithms for submodular problems with chance constraints. Our results show that these algorithms are highly effective when using surrogate functions that estimate constraint violations based on Chernoff bounds. Furthermore, we investigate the behavior of the algorithms on popular social network problems and show that high quality solutions can still be obtained even if there are strong restrictions imposed by the chance constraint.

Escaping Local Optima using Crossover with Emergent or Reinforced Diversity

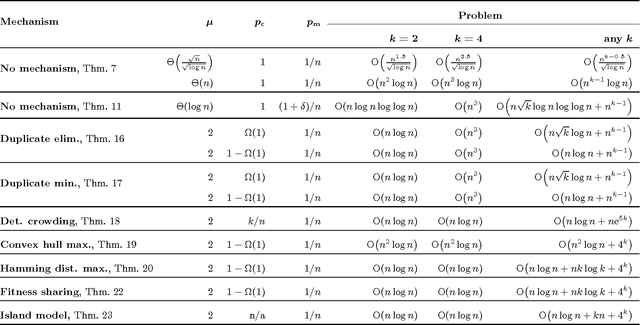
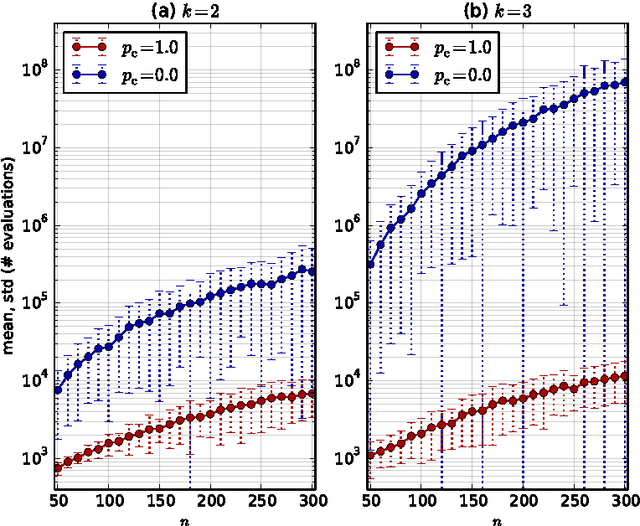
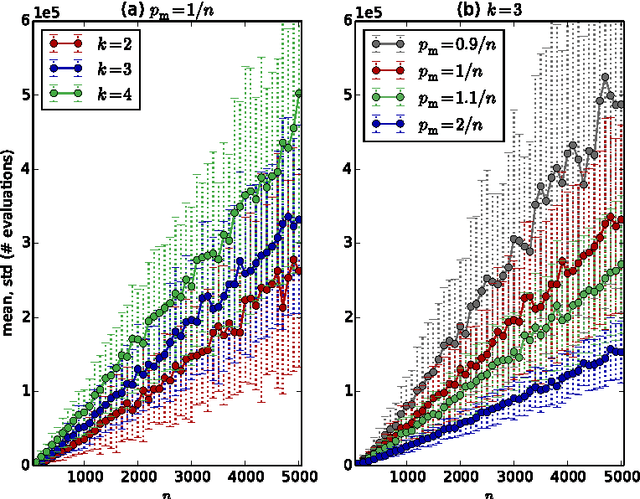
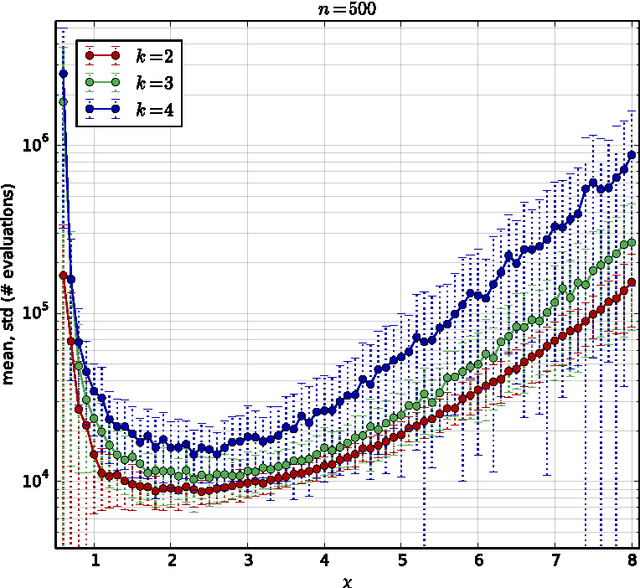
Population diversity is essential for avoiding premature convergence in Genetic Algorithms (GAs) and for the effective use of crossover. Yet the dynamics of how diversity emerges in populations are not well understood. We use rigorous runtime analysis to gain insight into population dynamics and GA performance for the ($\mu$+1) GA and the $\text{Jump}_k$ test function. We show that the interplay of crossover and mutation may serve as a catalyst leading to a sudden burst of diversity. This leads to improvements of the expected optimisation time of order $\Omega(n/\log n)$ compared to mutation-only algorithms like (1+1) EA. Moreover, increasing the mutation rate by an arbitrarily small constant factor can facilitate the generation of diversity, leading to speedups of order $\Omega(n)$. We also compare seven commonly used diversity mechanisms and evaluate their impact on runtime bounds for the ($\mu$+1) GA. All previous results in this context only hold for unrealistically low crossover probability $p_c=O(k/n)$, while we give analyses for the setting of constant $p_c < 1$ in all but one case. For the typical case of constant $k > 2$ and constant $p_c$, we can compare the resulting expected runtimes for different diversity mechanisms assuming an optimal choice of $\mu$: $O(n^{k-1})$ for duplicate elimination/minim., $O(n^2\log n)$ for maximising the convex hull, $O(n\log n)$ for deterministic crowding (assuming $p_c = k/n$), $O(n\log n)$ for maximising Hamming distance, $O(n\log n)$ for fitness sharing, $O(n\log n)$ for single-receiver island model. This proves a sizeable advantage of all variants of the ($\mu$+1) GA compared to (1+1) EA, which requires time $\Theta(n^k)$. Experiments complement our theoretical findings and further highlight the benefits of crossover and diversity on $\text{Jump}_k$.

The Benefit of Sex in Noisy Evolutionary Search

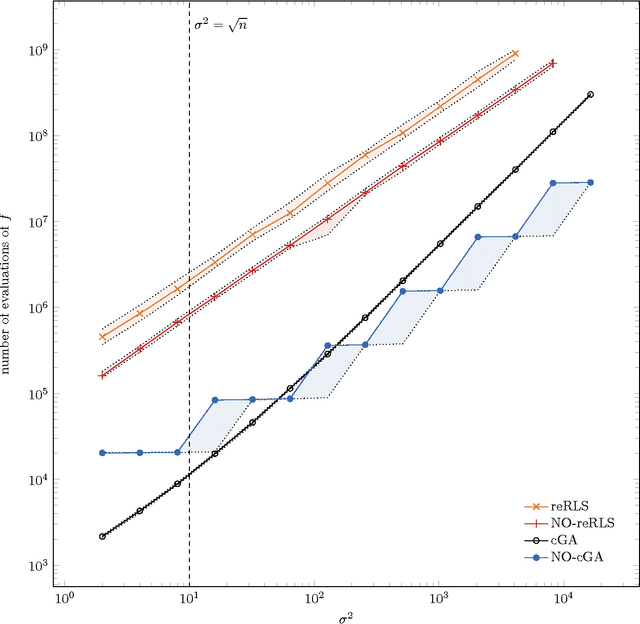
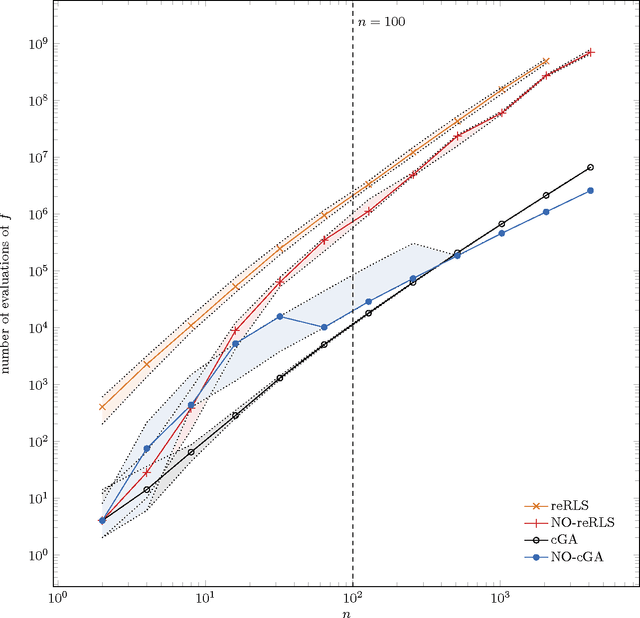
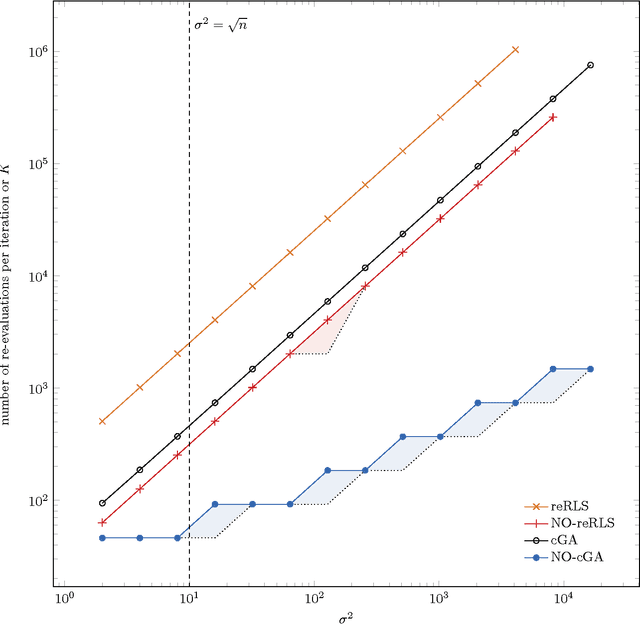
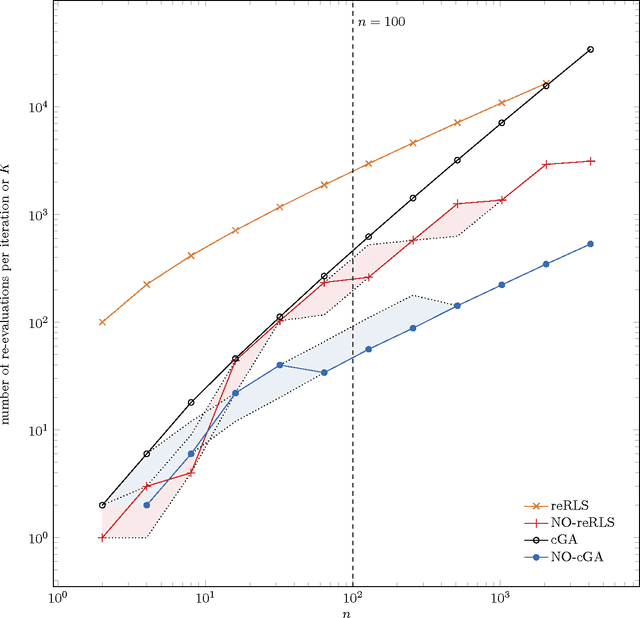
The benefit of sexual recombination is one of the most fundamental questions both in population genetics and evolutionary computation. It is widely believed that recombination helps solving difficult optimization problems. We present the first result, which rigorously proves that it is beneficial to use sexual recombination in an uncertain environment with a noisy fitness function. For this, we model sexual recombination with a simple estimation of distribution algorithm called the Compact Genetic Algorithm (cGA), which we compare with the classical $\mu+1$ EA. For a simple noisy fitness function with additive Gaussian posterior noise $\mathcal{N}(0,\sigma^2)$, we prove that the mutation-only $\mu+1$ EA typically cannot handle noise in polynomial time for $\sigma^2$ large enough while the cGA runs in polynomial time as long as the population size is not too small. This shows that in this uncertain environment sexual recombination is provably beneficial. We observe the same behavior in a small empirical study.

Parameterized Runtime Analyses of Evolutionary Algorithms for the Euclidean Traveling Salesperson Problem

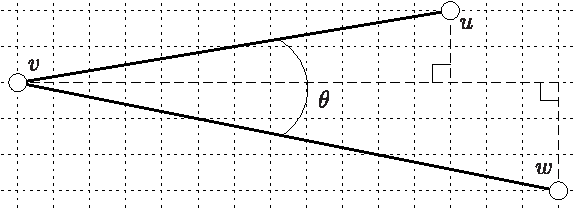
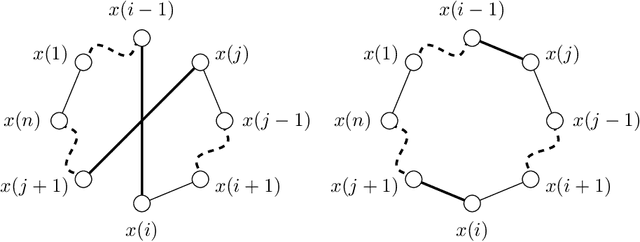
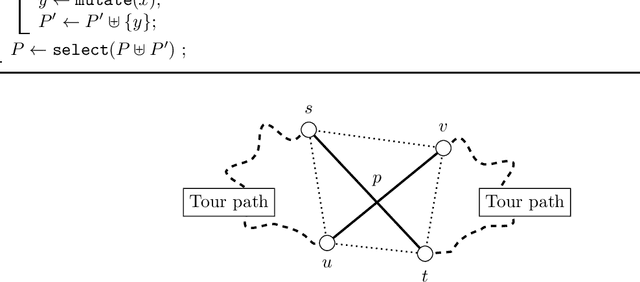
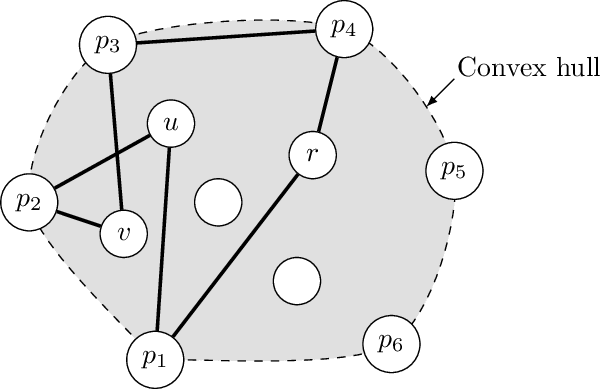
Parameterized runtime analysis seeks to understand the influence of problem structure on algorithmic runtime. In this paper, we contribute to the theoretical understanding of evolutionary algorithms and carry out a parameterized analysis of evolutionary algorithms for the Euclidean traveling salesperson problem (Euclidean TSP). We investigate the structural properties in TSP instances that influence the optimization process of evolutionary algorithms and use this information to bound the runtime of simple evolutionary algorithms. Our analysis studies the runtime in dependence of the number of inner points $k$ and shows that $(\mu + \lambda)$ evolutionary algorithms solve the Euclidean TSP in expected time $O((\mu/\lambda) \cdot n^3\gamma(\epsilon) + n\gamma(\epsilon) + (\mu/\lambda) \cdot n^{4k}(2k-1)!)$ where $\gamma$ is a function of the minimum angle $\epsilon$ between any three points. Finally, our analysis provides insights into designing a mutation operator that improves the upper bound on expected runtime. We show that a mixed mutation strategy that incorporates both 2-opt moves and permutation jumps results in an upper bound of $O((\mu/\lambda) \cdot n^3\gamma(\epsilon) + n\gamma(\epsilon) + (\mu/\lambda) \cdot n^{2k}(k-1)!)$ for the $(\mu+\lambda)$ EA.