Tight Runtime Guarantees From Understanding the Population Dynamics of the GSEMO Multi-Objective Evolutionary Algorithm

The global simple evolutionary multi-objective optimizer (GSEMO) is a simple, yet often effective multi-objective evolutionary algorithm (MOEA). By only maintaining non-dominated solutions, it has a variable population size that automatically adjusts to the needs of the optimization process. The downside of the dynamic population size is that the population dynamics of this algorithm are harder to understand, resulting, e.g., in the fact that only sporadic tight runtime analyses exist. In this work, we significantly enhance our understanding of the dynamics of the GSEMO, in particular, for the classic CountingOnesCountingZeros (COCZ) benchmark. From this, we prove a lower bound of order $\Omega(n^2 \log n)$, for the first time matching the seminal upper bounds known for over twenty years. We also show that the GSEMO finds any constant fraction of the Pareto front in time $O(n^2)$, improving over the previous estimate of $O(n^2 \log n)$ for the time to find the first Pareto optimum. Our methods extend to other classic benchmarks and yield, e.g., the first $\Omega(n^{k+1})$ lower bound for the OJZJ benchmark in the case that the gap parameter is $k \in \{2,3\}$. We are therefore optimistic that our new methods will be useful in future mathematical analyses of MOEAs.

A Simplified Run Time Analysis of the Univariate Marginal Distribution Algorithm on LeadingOnes

With elementary means, we prove a stronger run time guarantee for the univariate marginal distribution algorithm (UMDA) optimizing the LeadingOnes benchmark function in the desirable regime with low genetic drift. If the population size is at least quasilinear, then, with high probability, the UMDA samples the optimum within a number of iterations that is linear in the problem size divided by the logarithm of the UMDA's selection rate. This improves over the previous guarantee, obtained by Dang and Lehre (2015) via the deep level-based population method, both in terms of the run time and by demonstrating further run time gains from small selection rates. With similar arguments as in our upper-bound analysis, we also obtain the first lower bound for this problem. Under similar assumptions, we prove that a bound that matches our upper bound up to constant factors holds with high probability.

Significance-based Estimation-of-Distribution Algorithms

Estimation-of-distribution algorithms (EDAs) are randomized search heuristics that maintain a probabilistic model of the solution space. This model is updated from iteration to iteration, based on the quality of the solutions sampled according to the model. As previous works show, this short-term perspective can lead to erratic updates of the model, in particular, to bit-frequencies approaching a random boundary value. Such frequencies take long to be moved back to the middle range, leading to significant performance losses. In order to overcome this problem, we propose a new EDA based on the classic compact genetic algorithm (cGA) that takes into account a longer history of samples and updates its model only with respect to information which it classifies as statistically significant. We prove that this significance-based compact genetic algorithm (sig-cGA) optimizes the commonly regarded benchmark functions OneMax, LeadingOnes, and BinVal all in $O(n\log n)$ time, a result shown for no other EDA or evolutionary algorithm so far. For the recently proposed scGA -- an EDA that tries to prevent erratic model updates by imposing a bias to the uniformly distributed model -- we prove that it optimizes OneMax only in a time exponential in the hypothetical population size $1/\rho$. Similarly, we show that the convex search algorithm cannot optimize OneMax in polynomial time.

The Benefit of Sex in Noisy Evolutionary Search

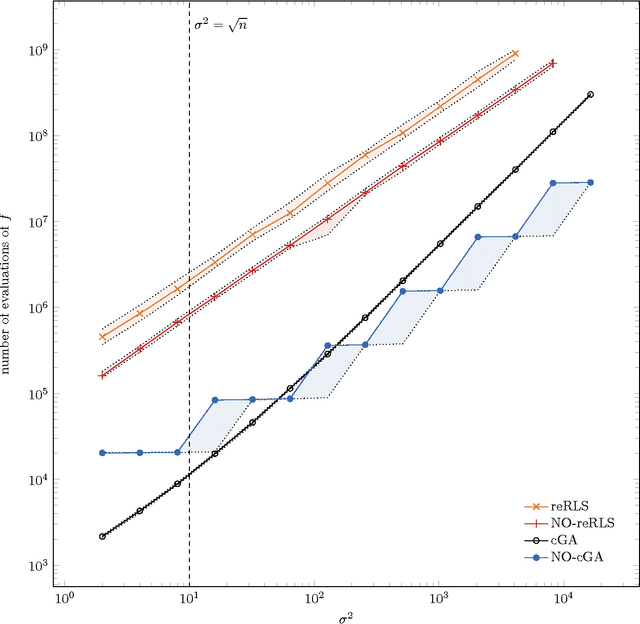
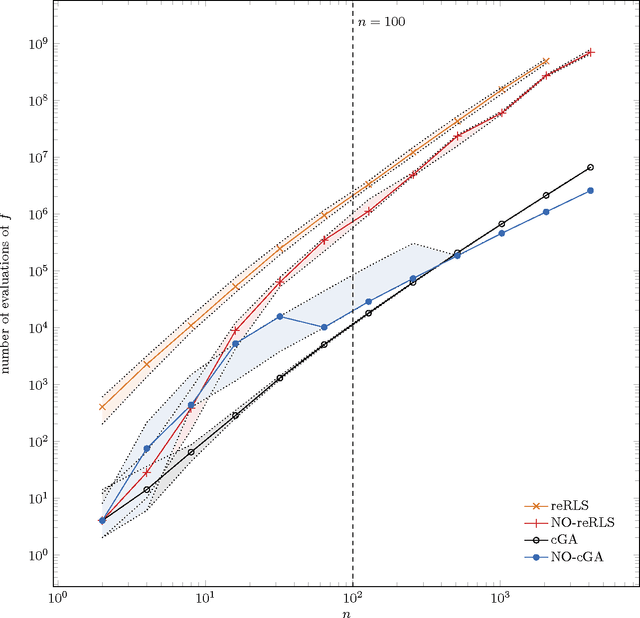
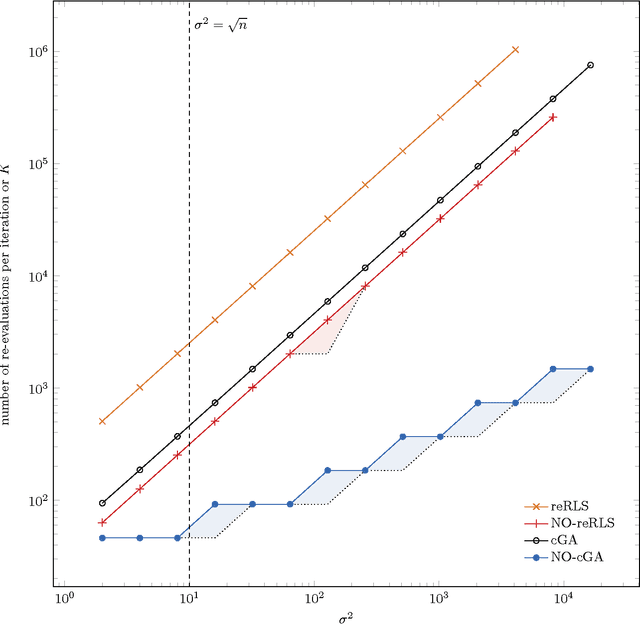
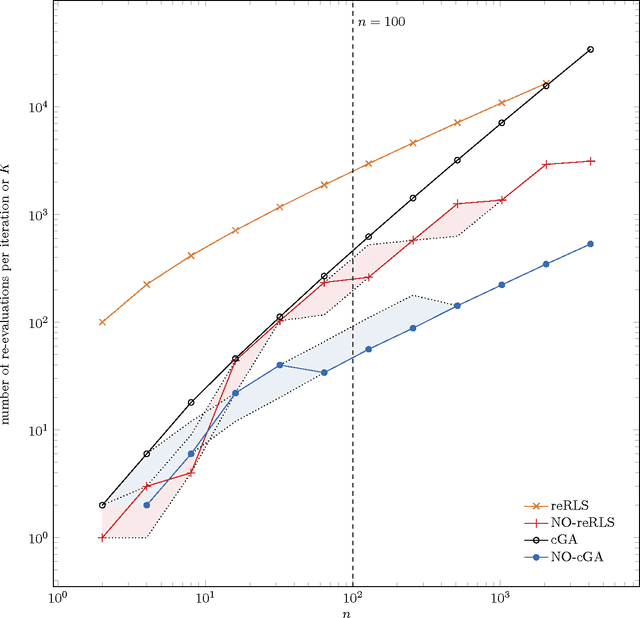
The benefit of sexual recombination is one of the most fundamental questions both in population genetics and evolutionary computation. It is widely believed that recombination helps solving difficult optimization problems. We present the first result, which rigorously proves that it is beneficial to use sexual recombination in an uncertain environment with a noisy fitness function. For this, we model sexual recombination with a simple estimation of distribution algorithm called the Compact Genetic Algorithm (cGA), which we compare with the classical $\mu+1$ EA. For a simple noisy fitness function with additive Gaussian posterior noise $\mathcal{N}(0,\sigma^2)$, we prove that the mutation-only $\mu+1$ EA typically cannot handle noise in polynomial time for $\sigma^2$ large enough while the cGA runs in polynomial time as long as the population size is not too small. This shows that in this uncertain environment sexual recombination is provably beneficial. We observe the same behavior in a small empirical study.