Evolutionary Algorithms Are Significantly More Robust to Noise When They Ignore It

Randomized search heuristics (RHSs) are generally believed to be robust to noise. However, almost all mathematical analyses on how RSHs cope with a noisy access to the objective function assume that each solution is re-evaluated whenever it is compared to others. This is unfortunate, both because it wastes computational resources and because it requires the user to foresee that noise is present (as in a noise-free setting, one would never re-evaluate solutions). In this work, we show the need for re-evaluations could be overestimated, and in fact, detrimental. For the classic benchmark problem of how the $(1+1)$ evolutionary algorithm optimizes the LeadingOnes benchmark, we show that without re-evaluations up to constant noise rates can be tolerated, much more than the $O(n^{-2} \log n)$ noise rates that can be tolerated when re-evaluating solutions. This first runtime analysis of an evolutionary algorithm solving a single-objective noisy problem without re-evaluations could indicate that such algorithms cope with noise much better than previously thought, and without the need to foresee the presence of noise.

Local Optima in Diversity Optimization: Non-trivial Offspring Population is Essential

The main goal of diversity optimization is to find a diverse set of solutions which satisfy some lower bound on their fitness. Evolutionary algorithms (EAs) are often used for such tasks, since they are naturally designed to optimize populations of solutions. This approach to diversity optimization, called EDO, has been previously studied from theoretical perspective, but most studies considered only EAs with a trivial offspring population such as the $(\mu + 1)$ EA. In this paper we give an example instance of a $k$-vertex cover problem, which highlights a critical difference of the diversity optimization from the regular single-objective optimization, namely that there might be a locally optimal population from which we can escape only by replacing at least two individuals at once, which the $(\mu + 1)$ algorithms cannot do. We also show that the $(\mu + \lambda)$ EA with $\lambda \ge \mu$ can effectively find a diverse population on $k$-vertex cover, if using a mutation operator inspired by Branson and Sutton (TCS 2023). To avoid the problem of subset selection which arises in the $(\mu + \lambda)$ EA when it optimizes diversity, we also propose the $(1_\mu + 1_\mu)$ EA$_D$, which is an analogue of the $(1 + 1)$ EA for populations, and which is also efficient at optimizing diversity on the $k$-vertex cover problem.

Runtime Analysis of Evolutionary Diversity Optimization on the Multi-objective (LeadingOnes, TrailingZeros) Problem

The diversity optimization is the class of optimization problems, in which we aim at finding a diverse set of good solutions. One of the frequently used approaches to solve such problems is to use evolutionary algorithms which evolve a desired diverse population. This approach is called evolutionary diversity optimization (EDO). In this paper, we analyse EDO on a 3-objective function LOTZ$_k$, which is a modification of the 2-objective benchmark function (LeadingOnes, TrailingZeros). We prove that the GSEMO computes a set of all Pareto-optimal solutions in $O(kn^3)$ expected iterations. We also analyze the runtime of the GSEMO$_D$ (a modification of the GSEMO for diversity optimization) until it finds a population with the best possible diversity for two different diversity measures, the total imbalance and the sorted imbalances vector. For the first measure we show that the GSEMO$_D$ optimizes it asymptotically faster than it finds a Pareto-optimal population, in $O(kn^2\log(n))$ expected iterations, and for the second measure we show an upper bound of $O(k^2n^3\log(n))$ expected iterations. We complement our theoretical analysis with an empirical study, which shows a very similar behavior for both diversity measures that is close to the theory predictions.

Using 3-Objective Evolutionary Algorithms for the Dynamic Chance Constrained Knapsack Problem

Real-world optimization problems often involve stochastic and dynamic components. Evolutionary algorithms are particularly effective in these scenarios, as they can easily adapt to uncertain and changing environments but often uncertainty and dynamic changes are studied in isolation. In this paper, we explore the use of 3-objective evolutionary algorithms for the chance constrained knapsack problem with dynamic constraints. In our setting, the weights of the items are stochastic and the knapsack's capacity changes over time. We introduce a 3-objective formulation that is able to deal with the stochastic and dynamic components at the same time and is independent of the confidence level required for the constraint. This new approach is then compared to the 2-objective formulation which is limited to a single confidence level. We evaluate the approach using two different multi-objective evolutionary algorithms (MOEAs), namely the global simple evolutionary multi-objective optimizer (GSEMO) and the multi-objective evolutionary algorithm based on decomposition (MOEA/D), across various benchmark scenarios. Our analysis highlights the advantages of the 3-objective formulation over the 2-objective formulation in addressing the dynamic chance constrained knapsack problem.

Already Moderate Population Sizes Provably Yield Strong Robustness to Noise

Experience shows that typical evolutionary algorithms can cope well with stochastic disturbances such as noisy function evaluations. In this first mathematical runtime analysis of the $(1+\lambda)$ and $(1,\lambda)$ evolutionary algorithms in the presence of prior bit-wise noise, we show that both algorithms can tolerate constant noise probabilities without increasing the asymptotic runtime on the OneMax benchmark. For this, a population size $\lambda$ suffices that is at least logarithmic in the problem size $n$. The only previous result in this direction regarded the less realistic one-bit noise model, required a population size super-linear in the problem size, and proved a runtime guarantee roughly cubic in the noiseless runtime for the OneMax benchmark. Our significantly stronger results are based on the novel proof argument that the noiseless offspring can be seen as a biased uniform crossover between the parent and the noisy offspring. We are optimistic that the technical lemmas resulting from this insight will find applications also in future mathematical runtime analyses of evolutionary algorithms.

Rigorous Runtime Analysis of Diversity Optimization with GSEMO on OneMinMax

The evolutionary diversity optimization aims at finding a diverse set of solutions which satisfy some constraint on their fitness. In the context of multi-objective optimization this constraint can require solutions to be Pareto-optimal. In this paper we study how the GSEMO algorithm with additional diversity-enhancing heuristic optimizes a diversity of its population on a bi-objective benchmark problem OneMinMax, for which all solutions are Pareto-optimal. We provide a rigorous runtime analysis of the last step of the optimization, when the algorithm starts with a population with a second-best diversity, and prove that it finds a population with optimal diversity in expected time $O(n^2)$, when the problem size $n$ is odd. For reaching our goal, we analyse the random walk of the population, which reflects the frequency of changes in the population and their outcomes.

Larger Offspring Populations Help the $(1 + (λ, λ))$ Genetic Algorithm to Overcome the Noise

Evolutionary algorithms are known to be robust to noise in the evaluation of the fitness. In particular, larger offspring population sizes often lead to strong robustness. We analyze to what extent the $(1+(\lambda,\lambda))$ genetic algorithm is robust to noise. This algorithm also works with larger offspring population sizes, but an intermediate selection step and a non-standard use of crossover as repair mechanism could render this algorithm less robust than, e.g., the simple $(1+\lambda)$ evolutionary algorithm. Our experimental analysis on several classic benchmark problems shows that this difficulty does not arise. Surprisingly, in many situations this algorithm is even more robust to noise than the $(1+\lambda)$~EA.

Coevolutionary Pareto Diversity Optimization

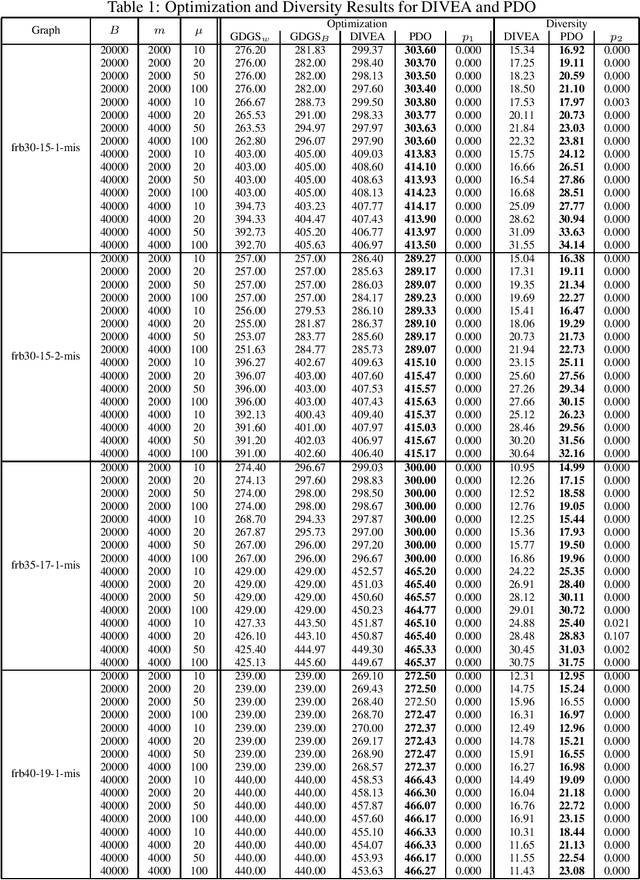
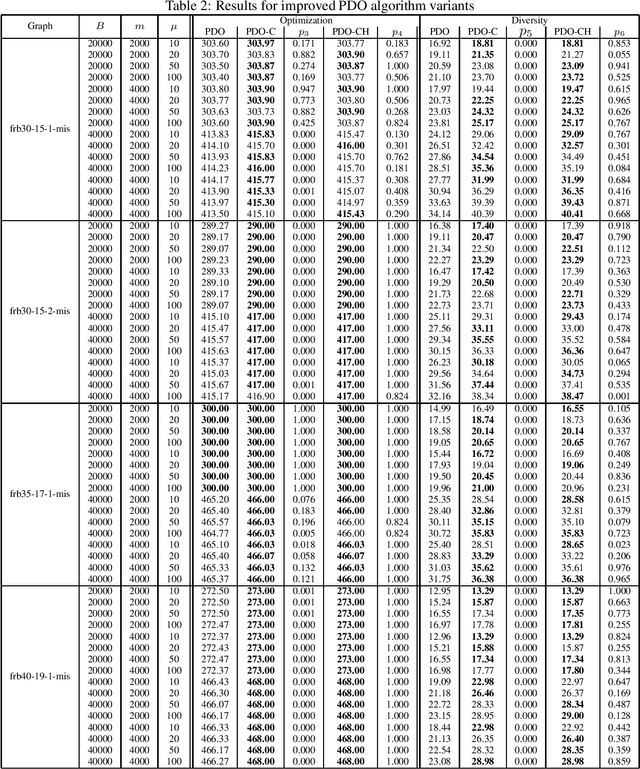
Computing diverse sets of high quality solutions for a given optimization problem has become an important topic in recent years. In this paper, we introduce a coevolutionary Pareto Diversity Optimization approach which builds on the success of reformulating a constrained single-objective optimization problem as a bi-objective problem by turning the constraint into an additional objective. Our new Pareto Diversity optimization approach uses this bi-objective formulation to optimize the problem while also maintaining an additional population of high quality solutions for which diversity is optimized with respect to a given diversity measure. We show that our standard co-evolutionary Pareto Diversity Optimization approach outperforms the recently introduced DIVEA algorithm which obtains its initial population by generalized diversifying greedy sampling and improving the diversity of the set of solutions afterwards. Furthermore, we study possible improvements of the Pareto Diversity Optimization approach. In particular, we show that the use of inter-population crossover further improves the diversity of the set of solutions.

Lazy Parameter Tuning and Control: Choosing All Parameters Randomly From a Power-Law Distribution

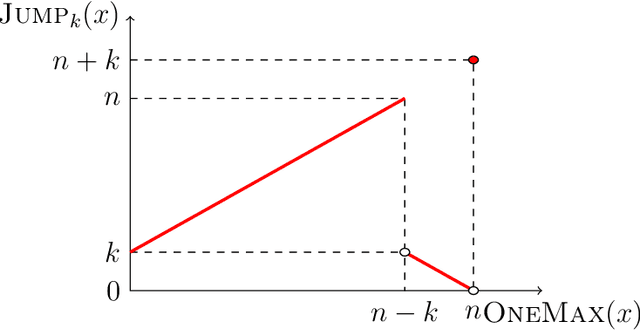
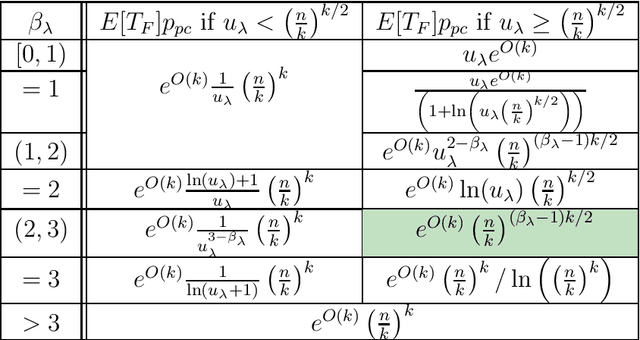
Most evolutionary algorithms have multiple parameters and their values drastically affect the performance. Due to the often complicated interplay of the parameters, setting these values right for a particular problem (parameter tuning) is a challenging task . This task becomes even more complicated when the optimal parameter values change significantly during the run of the algorithm since then a dynamic parameter choice (parameter control) is necessary. In this work, we propose a lazy but effective solution, namely choosing all parameter values (where this makes sense) in each iteration randomly from a suitably scaled power-law distribution. To demonstrate the effectiveness of this approach, we perform runtime analyses of the $(1+(\lambda,\lambda))$ genetic algorithm with all three parameters chosen in this manner. We show this algorithm on the one hand can imitate simple hill-climbers like the $(1+1)$ EA, giving the same asymptotic runtime on problems like OneMax, LeadingOnes, or Minimum Spanning Tree. On the other hand, this algorithm is also very efficient on jump functions, where the best static parameters are very different from those necessary to optimize simple problems. We prove a performance guarantee that is comparable, sometimes even better, than the best performance known for static parameters. We complement our theoretical results with a rigorous empirical study confirming what the asymptotic runtime results suggest.

First Steps Towards a Runtime Analysis When Starting With a Good Solution

The mathematical runtime analysis of evolutionary algorithms traditionally regards the time an algorithm needs to find a solution of a certain quality when initialized with a random population. In practical applications it may be possible to guess solutions that are better than random ones. We start a mathematical runtime analysis for such situations. We observe that different algorithms profit to a very different degree from a better initialization. We also show that the optimal parameterization of the algorithm can depend strongly on the quality of the initial solutions. To overcome this difficulty, self-adjusting and randomized heavy-tailed parameter choices can be profitable. Finally, we observe a larger gap between the performance of the best evolutionary algorithm we found and the corresponding black-box complexity. This could suggest that evolutionary algorithms better exploiting good initial solutions are still to be found. These first findings stem from analyzing the performance of the $(1+1)$ evolutionary algorithm and the static, self-adjusting, and heavy-tailed $(1 + (\lambda,\lambda))$ GA on the OneMax benchmark, but we are optimistic that the question how to profit from good initial solutions is interesting beyond these first examples.