Run Time Bounds for Integer-Valued OneMax Functions

While most theoretical run time analyses of discrete randomized search heuristics focused on finite search spaces, we consider the search space $\mathbb{Z}^n$. This is a further generalization of the search space of multi-valued decision variables $\{0,\ldots,r-1\}^n$. We consider as fitness functions the distance to the (unique) non-zero optimum $a$ (based on the $L_1$-metric) and the \ooea which mutates by applying a step-operator on each component that is determined to be varied. For changing by $\pm 1$, we show that the expected optimization time is $\Theta(n \cdot (|a|_{\infty} + \log(|a|_H)))$. In particular, the time is linear in the maximum value of the optimum $a$. Employing a different step operator which chooses a step size from a distribution so heavy-tailed that the expectation is infinite, we get an optimization time of $O(n \cdot \log^2 (|a|_1) \cdot \left(\log (\log (|a|_1))\right)^{1 + \epsilon})$. Furthermore, we show that RLS with step size adaptation achieves an optimization time of $\Theta(n \cdot \log(|a|_1))$. We conclude with an empirical analysis, comparing the above algorithms also with a variant of CMA-ES for discrete search spaces.

Analysis of the EA on LeadingOnes with Constraints

Understanding how evolutionary algorithms perform on constrained problems has gained increasing attention in recent years. In this paper, we study how evolutionary algorithms optimize constrained versions of the classical LeadingOnes problem. We first provide a run time analysis for the classical (1+1) EA on the LeadingOnes problem with a deterministic cardinality constraint, giving $\Theta(n (n-B)\log(B) + n^2)$ as the tight bound. Our results show that the behaviour of the algorithm is highly dependent on the constraint bound of the uniform constraint. Afterwards, we consider the problem in the context of stochastic constraints and provide insights using experimental studies on how the ($\mu$+1) EA is able to deal with these constraints in a sampling-based setting.

ELEA -- Build your own Evolutionary Algorithm in your Browser

We provide an open source framework to experiment with evolutionary algorithms which we call "Experimenting and Learning toolkit for Evolutionary Algorithms (ELEA)". ELEA is browser-based and allows to assemble evolutionary algorithms using drag-and-drop, starting from a number of simple pre-designed examples, making the startup costs for employing the toolkit minimal. The designed examples can be executed and collected data can be displayed graphically. Further features include export of algorithm designs and experimental results as well as multi-threading. With the very intuitive user interface and the short time to get initial experiments going, this tool is especially suitable for explorative analyses of algorithms as well as for the use in classrooms.

Theoretical Study of Optimizing Rugged Landscapes with the cGA

Estimation of distribution algorithms (EDAs) provide a distribution - based approach for optimization which adapts its probability distribution during the run of the algorithm. We contribute to the theoretical understanding of EDAs and point out that their distribution approach makes them more suitable to deal with rugged fitness landscapes than classical local search algorithms. Concretely, we make the OneMax function rugged by adding noise to each fitness value. The cGA can nevertheless find solutions with n(1 - \epsilon) many 1s, even for high variance of noise. In contrast to this, RLS and the (1+1) EA, with high probability, only find solutions with n(1/2+o(1)) many 1s, even for noise with small variance.

Lower Bounds from Fitness Levels Made Easy

One of the first and easy to use techniques for proving run time bounds for evolutionary algorithms is the so-called method of fitness levels by Wegener. It uses a partition of the search space into a sequence of levels which are traversed by the algorithm in increasing order, possibly skipping levels. An easy, but often strong upper bound for the run time can then be derived by adding the reciprocals of the probabilities to leave the levels (or upper bounds for these). Unfortunately, a similarly effective method for proving lower bounds has not yet been established. The strongest such method, proposed by Sudholt (2013), requires a careful choice of the viscosity parameters $\gamma_{i,j}$, $0 \le i < j \le n$. In this paper we present two new variants of the method, one for upper and one for lower bounds. Besides the level leaving probabilities, they only rely on the probabilities that levels are visited at all. We show that these can be computed or estimated without greater difficulties and apply our method to reprove the following known results in an easy and natural way. (i) The precise run time of the (1+1) EA on \textsc{LeadingOnes}. (ii) A lower bound for the run time of the (1+1) EA on \textsc{OneMax}, tight apart from an $O(n)$ term. (iii) A lower bound for the run time of the (1+1) EA on long $k$-paths. We also prove a tighter lower bound for the run time of the (1+1) EA on jump functions by showing that, regardless of the jump size, only with probability $O(2^{-n})$ the algorithm can avoid to jump over the valley of low fitness.

Maps for Learning Indexable Classes

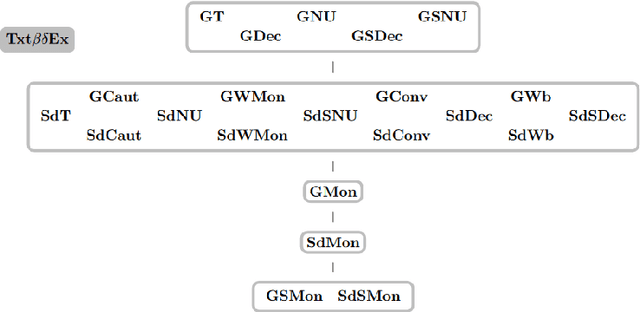
We study learning of indexed families from positive data where a learner can freely choose a hypothesis space (with uniformly decidable membership) comprising at least the languages to be learned. This abstracts a very universal learning task which can be found in many areas, for example learning of (subsets of) regular languages or learning of natural languages. We are interested in various restrictions on learning, such as consistency, conservativeness or set-drivenness, exemplifying various natural learning restrictions. Building on previous results from the literature, we provide several maps (depictions of all pairwise relations) of various groups of learning criteria, including a map for monotonicity restrictions and similar criteria and a map for restrictions on data presentation. Furthermore, we consider, for various learning criteria, whether learners can be assumed consistent.

Normal Forms for Witness-Based Learners in Inductive Inference

We study learners (computable devices) inferring formal languages, a setting referred to as language learning in the limit or inductive inference. In particular, we require the learners we investigate to be witness-based, that is, to justify each of their mind changes. Besides being a natural requirement for a learning task, this restriction deserves special attention as it is a specialization of various important learning paradigms. In particular, with the help of witness-based learning, explanatory learners are shown to be equally powerful under these seemingly incomparable paradigms. Nonetheless, until now, witness-based learners have only been studied sparsely. In this work, we conduct a thorough study of these learners both when requiring syntactic and semantic convergence and obtain normal forms thereof. In the former setting, we extend known results such that they include witness-based learning and generalize these to hold for a variety of learners. Transitioning to behaviourally correct learning, we also provide normal forms for semantically witness-based learners. Most notably, we show that set-driven globally semantically witness-based learners are equally powerful as their Gold-style semantically conservative counterpart. Such results are key to understanding the, yet undiscovered, mutual relation between various important learning paradigms when learning behaviourally correctly.

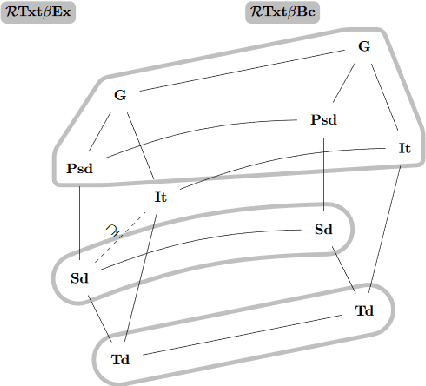
Mapping Monotonic Restrictions in Inductive Inference

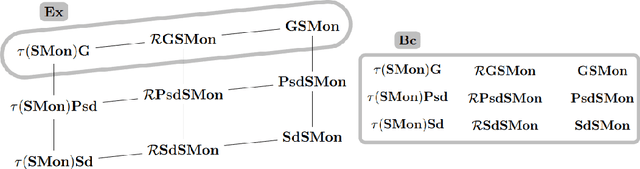
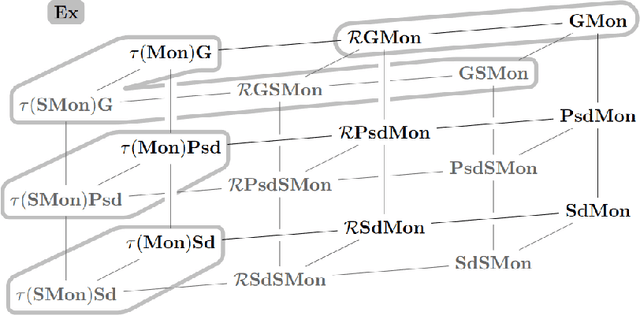
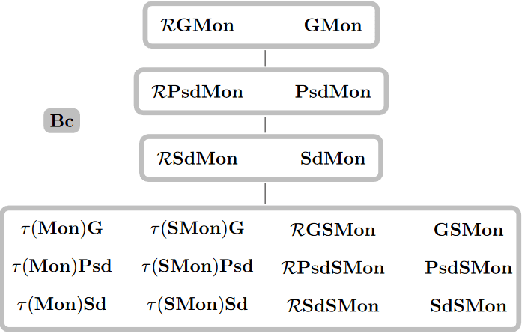
In language learning in the limit we investigate computable devices (learners) learning formal languages. Through the years, many natural restrictions have been imposed on the studied learners. As such, monotonic restrictions always enjoyed particular attention as, although being a natural requirement, monotonic learners show significantly diverse behaviour when studied in different settings. A recent study thoroughly analysed the learning capabilities of strongly monotone learners imposed with memory restrictions and various additional requirements. The unveiled differences between explanatory and behaviourally correct such learners motivate our studies of monotone learners dealing with the same restrictions. We reveal differences and similarities between monotone learners and their strongly monotone counterpart when studied with various additional restrictions. In particular, we show that explanatory monotone learners, although known to be strictly stronger, do (almost) preserve the pairwise relation as seen in strongly monotone learning. Contrasting this similarity, we find substantial differences when studying behaviourally correct monotone learners. Most notably, we show that monotone learners, as opposed to their strongly monotone counterpart, do heavily rely on the order the information is given in, an unusual result for behaviourally correct learners.

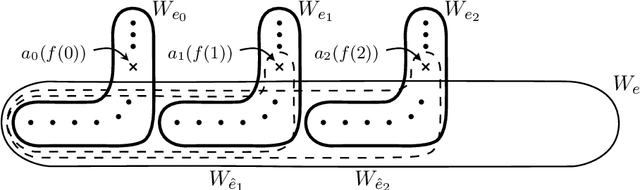
Learning Languages in the Limit from Positive Information with Finitely Many Memory Changes

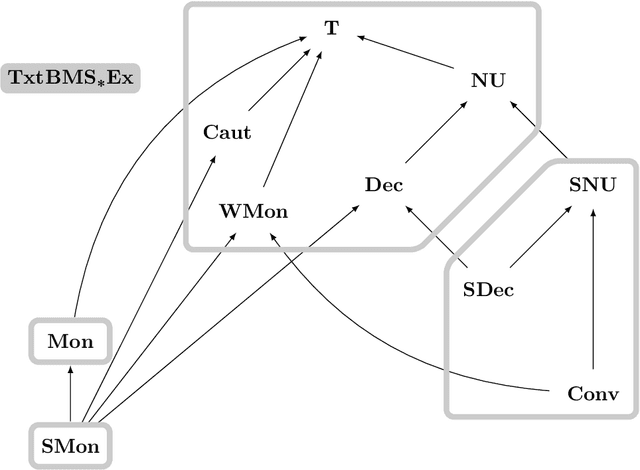
We investigate learning collections of languages from texts by an inductive inference machine with access to the current datum and its memory in form of states. The bounded memory states (BMS) learner is considered successful in case it eventually settles on a correct hypothesis while exploiting only finitely many different states. We give the complete map of all pairwise relations for an established collection of learning success restrictions. Most prominently, we show that non-U-shapedness is not restrictive, while conservativeness and (strong) monotonicity are. Some results carry over from iterative learning by a general lemma showing that, for a wealth of restrictions (the \emph{semantic} restrictions), iterative and bounded memory states learning are equivalent. We also give an example of a non-semantic restriction (strongly non-U-shapedness) where the two settings differ.

Learning Half-Spaces and other Concept Classes in the Limit with Iterative Learners

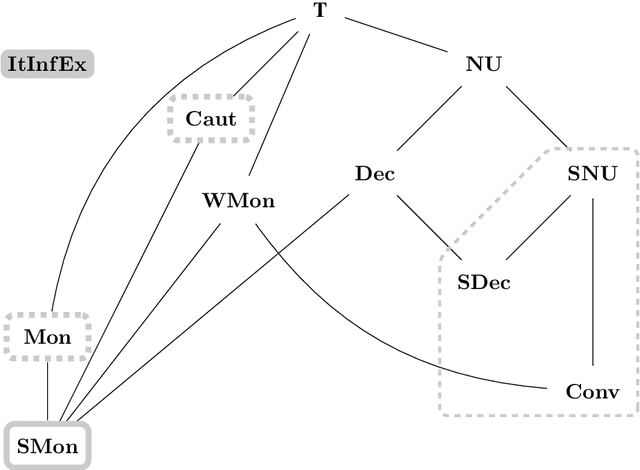
In order to model an efficient learning paradigm, iterative learning algorithms access data one by one, updating the current hypothesis without regress to past data. Past research on iterative learning analyzed for example many important additional requirements and their impact on iterative learners. In this paper, our results are twofold. First, we analyze the relative learning power of various settings of iterative learning, including learning from text and from informant, as well as various further restrictions, for example we show that strongly non-U-shaped learning is restrictive for iterative learning from informant. Second, we investigate the learnability of the concept class of half-spaces and provide a constructive iterative algorithm to learn the set of half-spaces from informant.