Andrew Anderson
From Verification Burden to Trusted Collaboration: Design Goals for LLM-Assisted Literature Reviews
Dec 12, 2025


Abstract:Large Language Models (LLMs) are increasingly embedded in academic writing practices. Although numerous studies have explored how researchers employ these tools for scientific writing, their concrete implementation, limitations, and design challenges within the literature review process remain underexplored. In this paper, we report a user study with researchers across multiple disciplines to characterize current practices, benefits, and \textit{pain points} in using LLMs to investigate related work. We identified three recurring gaps: (i) lack of trust in outputs, (ii) persistent verification burden, and (iii) requiring multiple tools. This motivates our proposal of six design goals and a high-level framework that operationalizes them through improved related papers visualization, verification at every step, and human-feedback alignment with generation-guided explanations. Overall, by grounding our work in the practical, day-to-day needs of researchers, we designed a framework that addresses these limitations and models real-world LLM-assisted writing, advancing trust through verifiable actions and fostering practical collaboration between researchers and AI systems.
"Over-the-Hood" AI Inclusivity Bugs and How 3 AI Product Teams Found and Fixed Them
Oct 21, 2025Abstract:While much research has shown the presence of AI's "under-the-hood" biases (e.g., algorithmic, training data, etc.), what about "over-the-hood" inclusivity biases: barriers in user-facing AI products that disproportionately exclude users with certain problem-solving approaches? Recent research has begun to report the existence of such biases -- but what do they look like, how prevalent are they, and how can developers find and fix them? To find out, we conducted a field study with 3 AI product teams, to investigate what kinds of AI inclusivity bugs exist uniquely in user-facing AI products, and whether/how AI product teams might harness an existing (non-AI-oriented) inclusive design method to find and fix them. The teams' work resulted in identifying 6 types of AI inclusivity bugs arising 83 times, fixes covering 47 of these bug instances, and a new variation of the GenderMag inclusive design method, GenderMag-for-AI, that is especially effective at detecting certain kinds of AI inclusivity bugs.
Domino Saliency Metrics: Improving Existing Channel Saliency Metrics with Structural Information
May 04, 2022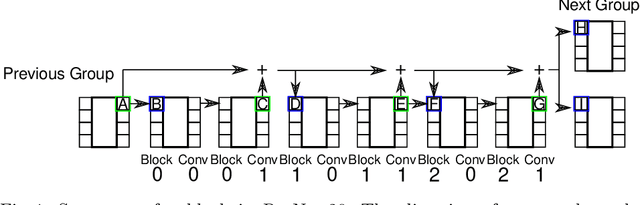
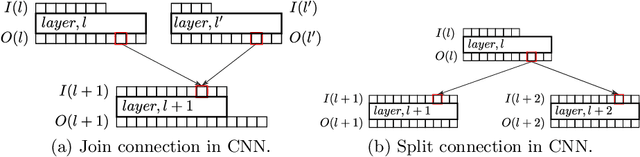
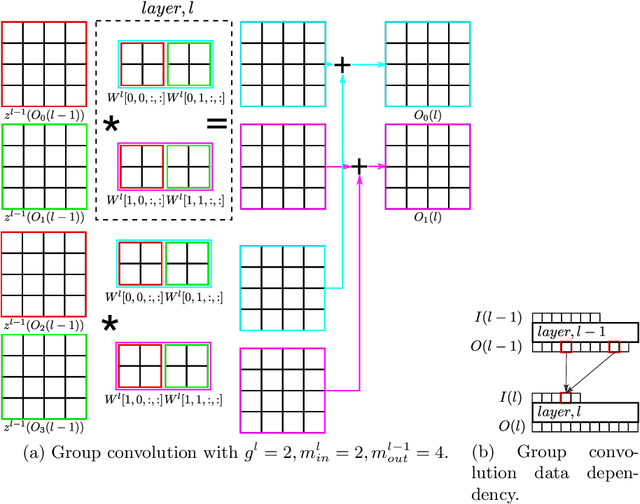
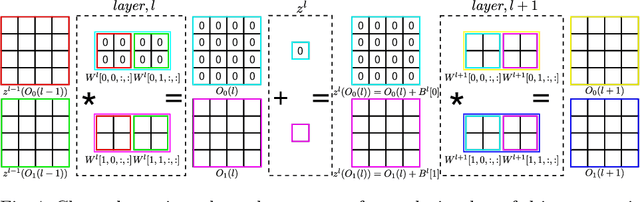
Abstract:Channel pruning is used to reduce the number of weights in a Convolutional Neural Network (CNN). Channel pruning removes slices of the weight tensor so that the convolution layer remains dense. The removal of these weight slices from a single layer causes mismatching number of feature maps between layers of the network. A simple solution is to force the number of feature map between layers to match through the removal of weight slices from subsequent layers. This additional constraint becomes more apparent in DNNs with branches where multiple channels need to be pruned together to keep the network dense. Popular pruning saliency metrics do not factor in the structural dependencies that arise in DNNs with branches. We propose Domino metrics (built on existing channel saliency metrics) to reflect these structural constraints. We test Domino saliency metrics against the baseline channel saliency metrics on multiple networks with branches. Domino saliency metrics improved pruning rates in most tested networks and up to 25% in AlexNet on CIFAR-10.
Winograd Convolution for Deep Neural Networks: Efficient Point Selection
Jan 25, 2022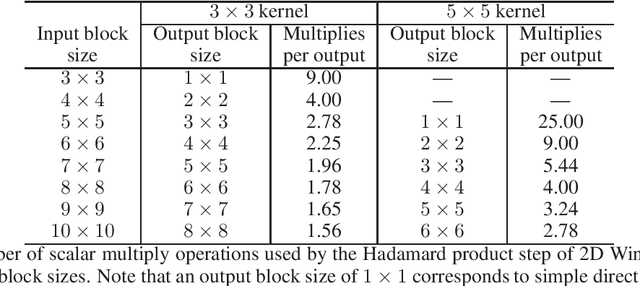
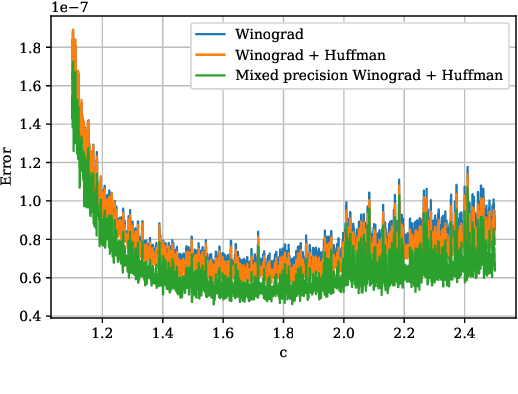
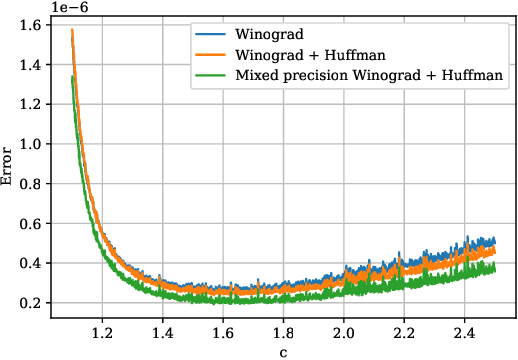

Abstract:Convolutional neural networks (CNNs) have dramatically improved the accuracy of tasks such as object recognition, image segmentation and interactive speech systems. CNNs require large amounts of computing resources because ofcomputationally intensive convolution layers. Fast convolution algorithms such as Winograd convolution can greatly reduce the computational cost of these layers at a cost of poor numeric properties, such that greater savings in computation exponentially increase floating point errors. A defining feature of each Winograd convolution algorithm is a set of real-value points where polynomials are sampled. The choice of points impacts the numeric accuracy of the algorithm, but the optimal set of points for small convolutions remains unknown. Existing work considers only small integers and simple fractions as candidate points. In this work, we propose a novel approach to point selection using points of the form {-1/c , -c, c, 1/c } using the full range of real-valued numbers for c. We show that groups of this form cause cancellations in the Winograd transform matrices that reduce numeric error. We find empirically that the error for different values of c forms a rough curve across the range of real-value numbers helping to localize the values of c that reduce error and that lower errors can be achieved with non-obvious real-valued evaluation points instead of integers or simple fractions. We study a range of sizes for small convolutions and achieve reduction in error ranging from 2% to around 59% for both 1D and 2D convolution. Furthermore, we identify patterns in cases when we select a subset of our proposed points which will always lead to a lower error. Finally we implement a complete Winograd convolution layer and use it to run deep convolution neural networks on real datasets and show that our proposed points reduce error, ranging from 22% to 63%.
TASO: Time and Space Optimization for Memory-Constrained DNN Inference
May 21, 2020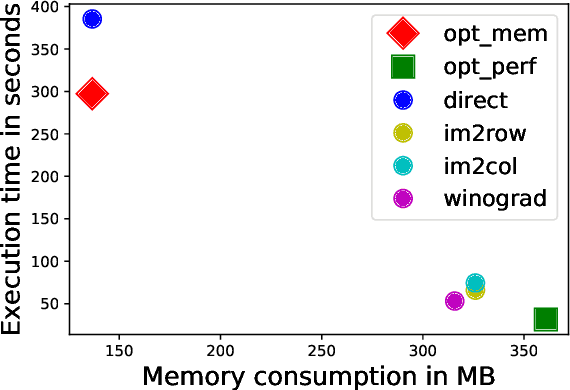
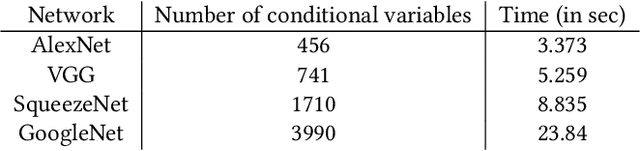

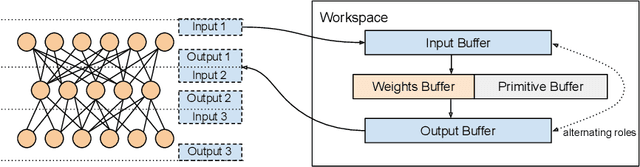
Abstract:Convolutional neural networks (CNNs) are used in many embedded applications, from industrial robotics and automation systems to biometric identification on mobile devices. State-of-the-art classification is typically achieved by large networks, which are prohibitively expensive to run on mobile and embedded devices with tightly constrained memory and energy budgets. We propose an approach for ahead-of-time domain specific optimization of CNN models, based on an integer linear programming (ILP) for selecting primitive operations to implement convolutional layers. We optimize the trade-off between execution time and memory consumption by: 1) attempting to minimize execution time across the whole network by selecting data layouts and primitive operations to implement each layer; and 2) allocating an appropriate workspace that reflects the upper bound of memory footprint per layer. These two optimization strategies can be used to run any CNN on any platform with a C compiler. Our evaluation with a range of popular ImageNet neural architectures (GoogleNet, AlexNet, VGG, ResNet and SqueezeNet) on the ARM Cortex-A15 yields speedups of 8x compared to a greedy algorithm based primitive selection, reduces memory requirement by 2.2x while sacrificing only 15% of inference time compared to a solver that considers inference time only. In addition, our optimization approach exposes a range of optimal points for different configurations across the Pareto frontier of memory and latency trade-off, which can be used under arbitrary system constraints.
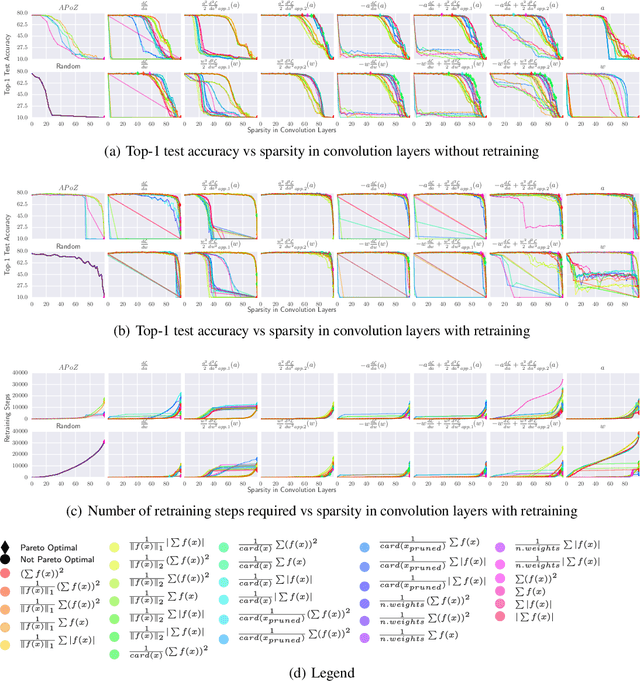
Composition of Saliency Metrics for Channel Pruning with a Myopic Oracle
Apr 03, 2020

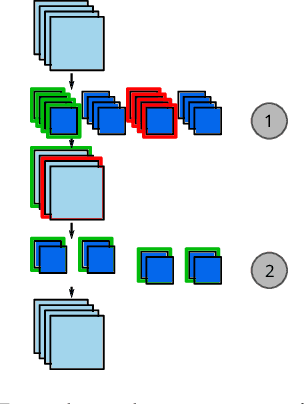
Abstract:The computation and memory needed for Convolutional Neural Network (CNN) inference can be reduced by pruning weights from the trained network. Pruning is guided by a pruning saliency, which heuristically approximates the change in the loss function associated with the removal of specific weights. Many pruning signals have been proposed, but the performance of each heuristic depends on the particular trained network. This leaves the data scientist with a difficult choice. When using any one saliency metric for the entire pruning process, we run the risk of the metric assumptions being invalidated, leading to poor decisions being made by the metric. Ideally we could combine the best aspects of different saliency metrics. However, despite an extensive literature review, we are unable to find any prior work on composing different saliency metrics. The chief difficulty lies in combining the numerical output of different saliency metrics, which are not directly comparable. We propose a method to compose several primitive pruning saliencies, to exploit the cases where each saliency measure does well. Our experiments show that the composition of saliencies avoids many poor pruning choices identified by individual saliencies. In most cases our method finds better selections than even the best individual pruning saliency.
Performance-Oriented Neural Architecture Search
Jan 09, 2020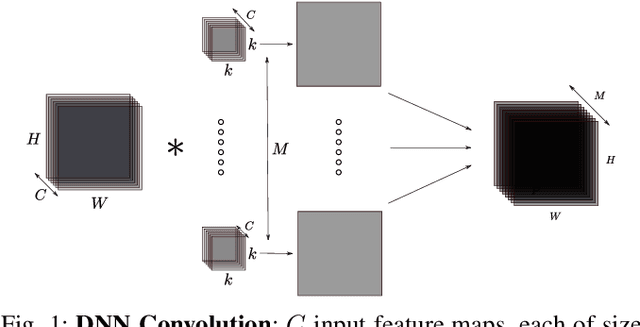
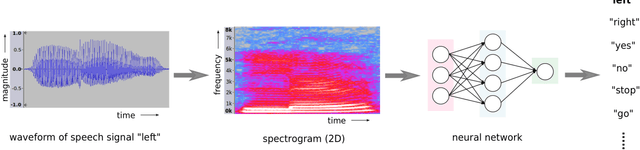

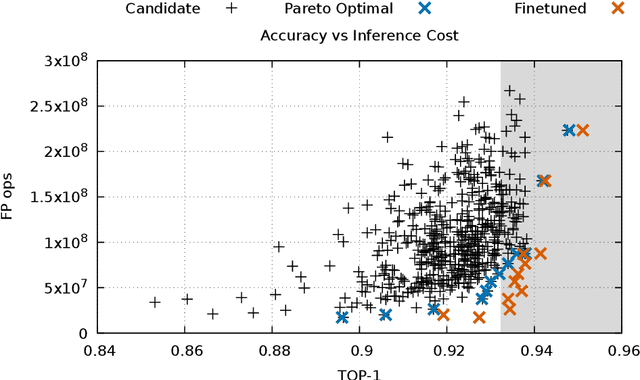
Abstract:Hardware-Software Co-Design is a highly successful strategy for improving performance of domain-specific computing systems. We argue for the application of the same methodology to deep learning; specifically, we propose to extend neural architecture search with information about the hardware to ensure that the model designs produced are highly efficient in addition to the typical criteria around accuracy. Using the task of keyword spotting in audio on edge computing devices, we demonstrate that our approach results in neural architecture that is not only highly accurate, but also efficiently mapped to the computing platform which will perform the inference. Using our modified neural architecture search, we demonstrate $0.88\%$ increase in TOP-1 accuracy with $1.85\times$ reduction in latency for keyword spotting in audio on an embedded SoC, and $1.59\times$ on a high-end GPU.
A Taxonomy of Channel Pruning Signals in CNNs
Jun 11, 2019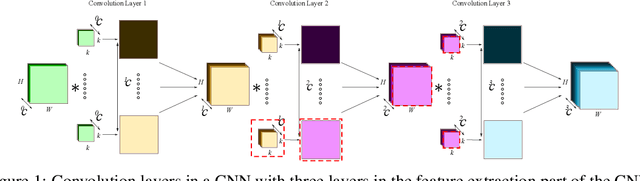


Abstract:Convolutional neural networks (CNNs) are widely used for classification problems. However, they often require large amounts of computation and memory which are not readily available in resource constrained systems. Pruning unimportant parameters from CNNs to reduce these requirements has been a subject of intensive research in recent years. However, novel approaches in pruning signals are sometimes difficult to compare against each other. We propose a taxonomy that classifies pruning signals based on four mostly-orthogonal components of the signal. We also empirically evaluate 396 pruning signals including existing ones, and new signals constructed from the components of existing signals. We find that some of our newly constructed signals outperform the best existing pruning signals.
Explaining Reinforcement Learning to Mere Mortals: An Empirical Study
Mar 22, 2019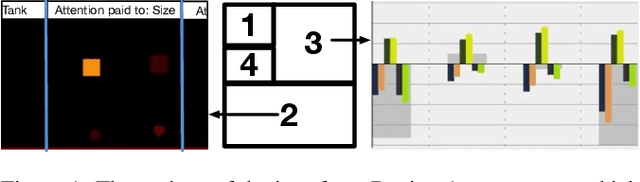
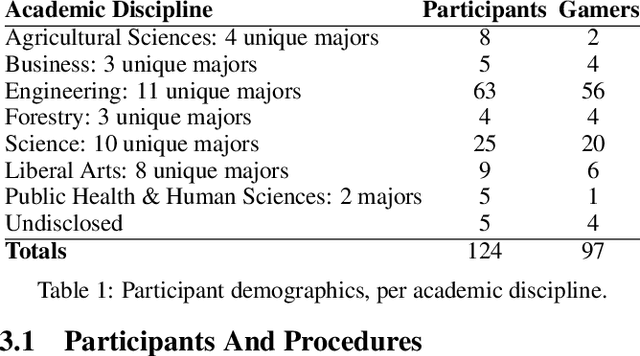
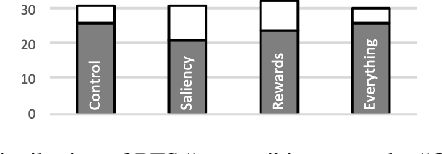
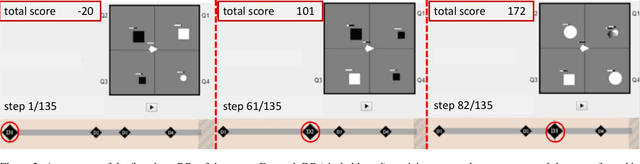
Abstract:We present a user study to investigate the impact of explanations on non-experts' understanding of reinforcement learning (RL) agents. We investigate both a common RL visualization, saliency maps (the focus of attention), and a more recent explanation type, reward-decomposition bars (predictions of future types of rewards). We designed a 124 participant, four-treatment experiment to compare participants' mental models of an RL agent in a simple Real-Time Strategy (RTS) game. Our results show that the combination of both saliency and reward bars were needed to achieve a statistically significant improvement in mental model score over the control. In addition, our qualitative analysis of the data reveals a number of effects for further study.
Optimal DNN Primitive Selection with Partitioned Boolean Quadratic Programming
Nov 02, 2018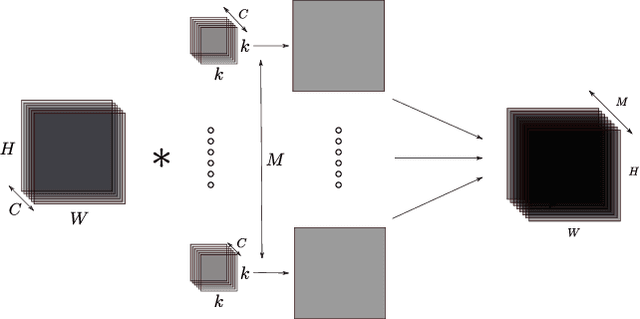
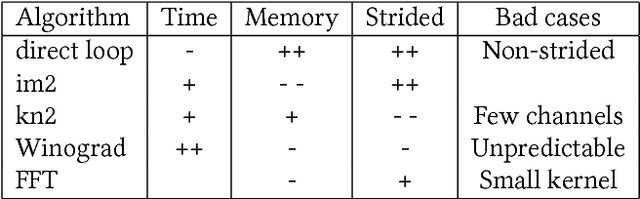
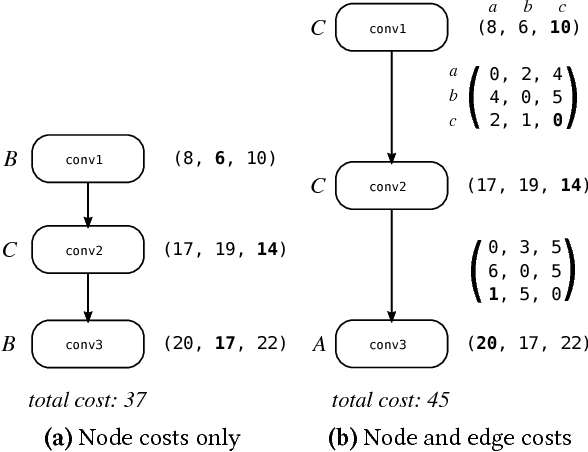
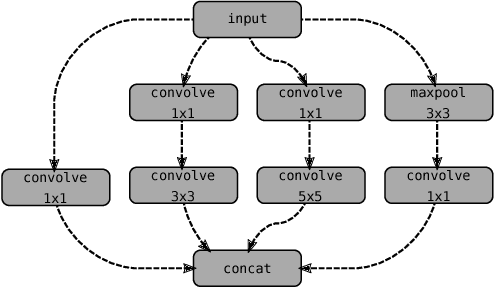
Abstract:Deep Neural Networks (DNNs) require very large amounts of computation both for training and for inference when deployed in the field. Many different algorithms have been proposed to implement the most computationally expensive layers of DNNs. Further, each of these algorithms has a large number of variants, which offer different trade-offs of parallelism, data locality, memory footprint, and execution time. In addition, specific algorithms operate much more efficiently on specialized data layouts and formats. We state the problem of optimal primitive selection in the presence of data format transformations, and show that it is NP-hard by demonstrating an embedding in the Partitioned Boolean Quadratic Assignment problem (PBQP). We propose an analytic solution via a PBQP solver, and evaluate our approach experimentally by optimizing several popular DNNs using a library of more than 70 DNN primitives, on an embedded platform and a general purpose platform. We show experimentally that significant gains are possible versus the state of the art vendor libraries by using a principled analytic solution to the problem of layout selection in the presence of data format transformations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge