Barbara Barabasz
Winograd Convolution for Deep Neural Networks: Efficient Point Selection
Jan 25, 2022

Abstract:Convolutional neural networks (CNNs) have dramatically improved the accuracy of tasks such as object recognition, image segmentation and interactive speech systems. CNNs require large amounts of computing resources because ofcomputationally intensive convolution layers. Fast convolution algorithms such as Winograd convolution can greatly reduce the computational cost of these layers at a cost of poor numeric properties, such that greater savings in computation exponentially increase floating point errors. A defining feature of each Winograd convolution algorithm is a set of real-value points where polynomials are sampled. The choice of points impacts the numeric accuracy of the algorithm, but the optimal set of points for small convolutions remains unknown. Existing work considers only small integers and simple fractions as candidate points. In this work, we propose a novel approach to point selection using points of the form {-1/c , -c, c, 1/c } using the full range of real-valued numbers for c. We show that groups of this form cause cancellations in the Winograd transform matrices that reduce numeric error. We find empirically that the error for different values of c forms a rough curve across the range of real-value numbers helping to localize the values of c that reduce error and that lower errors can be achieved with non-obvious real-valued evaluation points instead of integers or simple fractions. We study a range of sizes for small convolutions and achieve reduction in error ranging from 2% to around 59% for both 1D and 2D convolution. Furthermore, we identify patterns in cases when we select a subset of our proposed points which will always lead to a lower error. Finally we implement a complete Winograd convolution layer and use it to run deep convolution neural networks on real datasets and show that our proposed points reduce error, ranging from 22% to 63%.
Quantaized Winograd/Toom-Cook Convolution for DNNs: Beyond Canonical Polynomials Base
Apr 23, 2020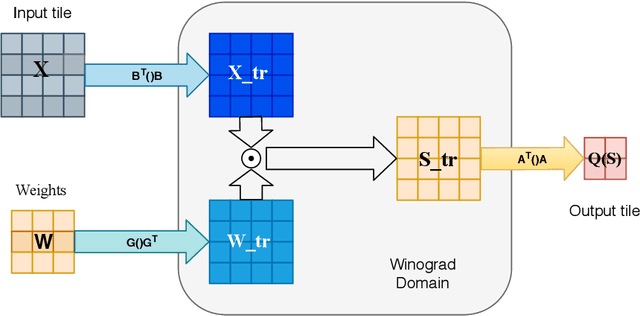

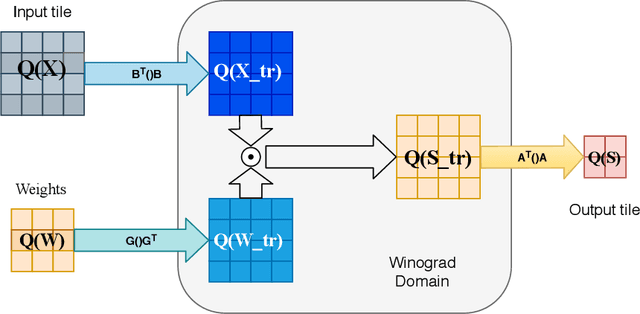

Abstract:The problem how to speed up the convolution computations in Deep Neural Networks is widely investigated in recent years. The Winograd convolution algorithm is a common used method that significantly reduces time consumption. However, it suffers from a problem with numerical accuracy particularly for lower precisions. In this paper we present the application of base change technique for quantized Winograd-aware training model. We show that we can train the $8$ bit quantized network to nearly the same accuracy (up to 0.5% loss) for tested network (Resnet18) and dataset (CIFAR10) as for quantized direct convolution with few additional operations in pre/post transformations. Keeping Hadamard product on $9$ bits allow us to obtain the same accuracy as for direct convolution.
Winograd Convolution for DNNs: Beyond linear polinomials
May 13, 2019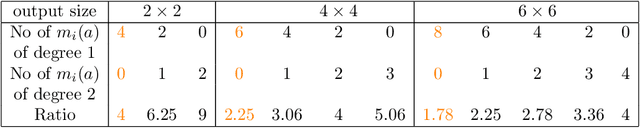
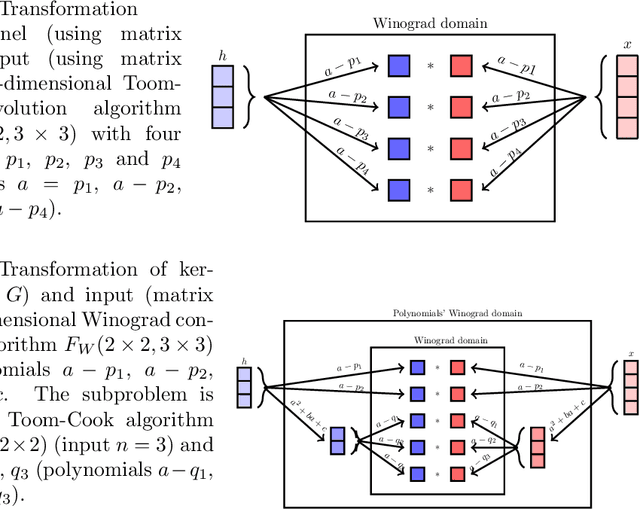
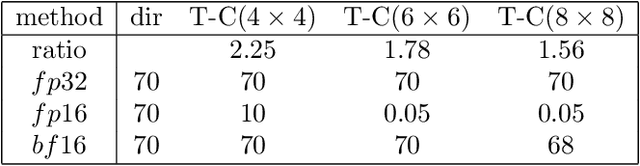
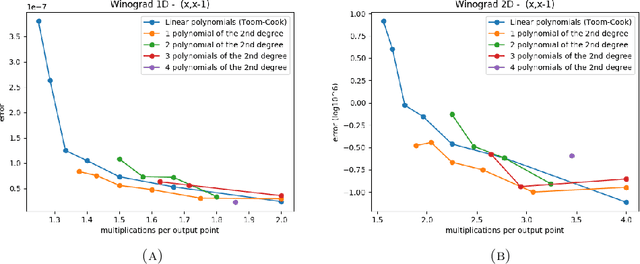
Abstract:We investigated a wider range of Winograd family convolution algorithms for Deep Neural Network. We presented the explicit Winograd convolution algorithm in general case (used the polynomials of the degrees higher than one). It allows us to construct more different versions in the aspect of performance than commonly used Winograd convolution algorithms and improve the accuracy and performance of convolution computations. We found that in $fp16$ this approach gives us better accuracy of image recognition while keeps the same number of general multiplications computed per single output point as the commonly used Winograd algorithm for a kernel of the size $3 \times 3$ and output size equal to $4 \times 4$. We demonstrated that in $bf16$ it is possible to perform the convolution computation faster keeping the accuracy of image recognition the same as for direct convolution method. We tested our approach for a subset of $2000$ images from Imaginet validation set. We present the results for three precision of computations $fp32$, $fp16$ and $bf16$.
Error Analysis and Improving the Accuracy of Winograd Convolution for Deep Neural Networks
Sep 22, 2018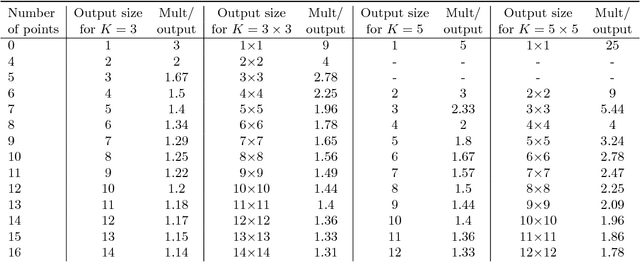
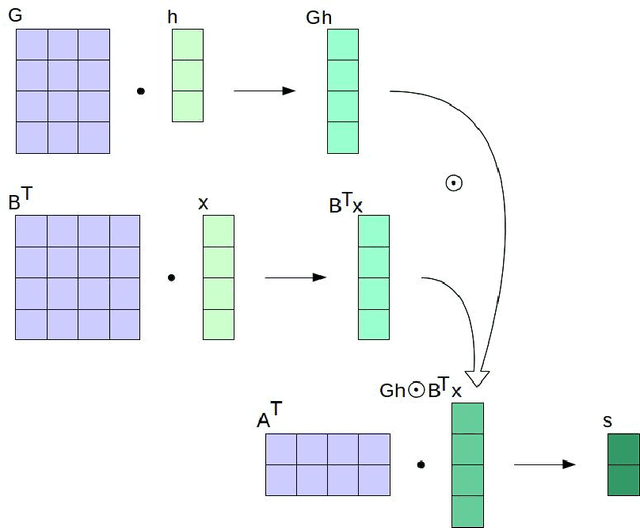
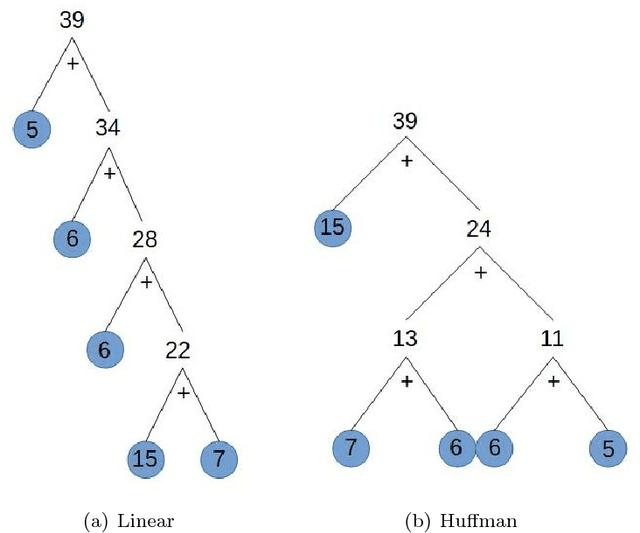
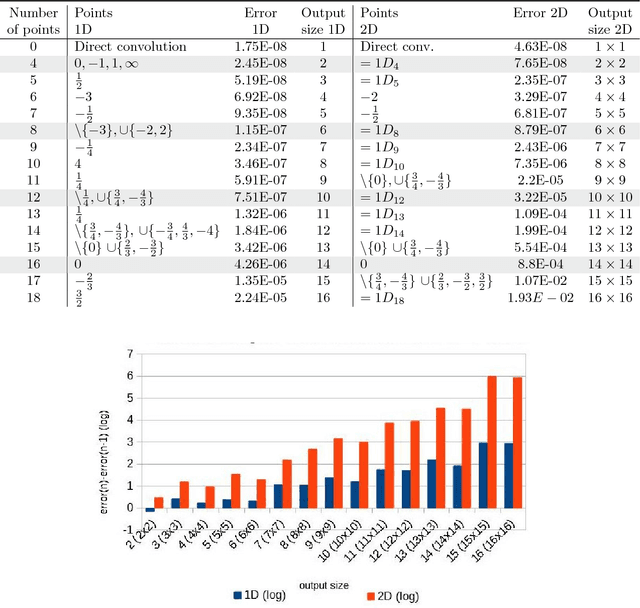
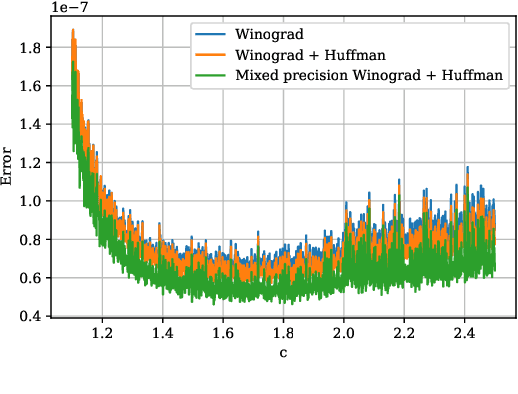
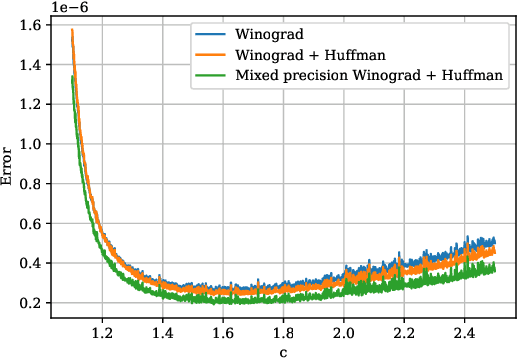
Abstract:Modern deep neural networks (DNNs) spend a large amount of their execution time computing convolutions. Winograd's minimal algorithm for small convolutions can greatly reduce the number of arithmetic operations. However, a large reduction in floating point (FP) operations in these algorithms can result in poor numeric accuracy. In this paper we analyse the FP error and prove boundaries on the error. We show that the "modified" algorithm gives a significantly better accuracy of the result. We propose several methods for reducing FP error of these algorithms. Minimal convolution algorithms depend on the selection of several numeric \textit{points} that have a large impact on the accuracy of the result. We propose a canonical evaluation ordering that both reduces FP error and the size of the search space based on Huffman coding. We study point selection experimentally, and find empirically good points. We also identify the main factors that associated with sets of points that result in a low error. In addition, we explore other methods to reduce FP error, including mixed-precision convolution, and pairwise addition across DNN channels. Using our methods we can significantly reduce FP error for a given block size, which allows larger block sizes and reduced computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge