Winograd Convolution for Deep Neural Networks: Efficient Point Selection

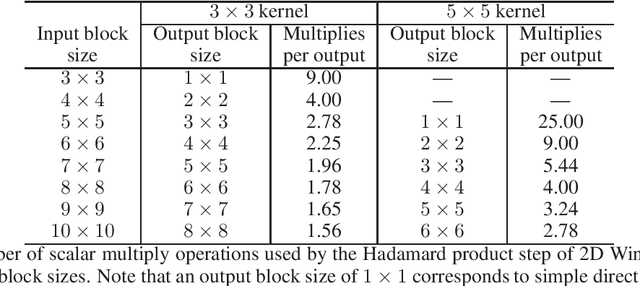
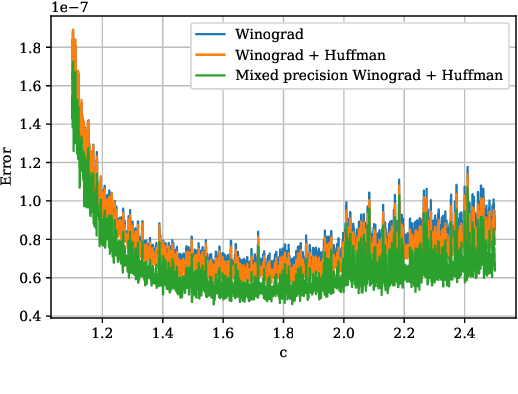
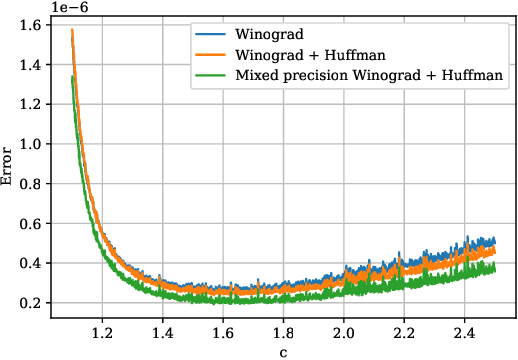
Convolutional neural networks (CNNs) have dramatically improved the accuracy of tasks such as object recognition, image segmentation and interactive speech systems. CNNs require large amounts of computing resources because ofcomputationally intensive convolution layers. Fast convolution algorithms such as Winograd convolution can greatly reduce the computational cost of these layers at a cost of poor numeric properties, such that greater savings in computation exponentially increase floating point errors. A defining feature of each Winograd convolution algorithm is a set of real-value points where polynomials are sampled. The choice of points impacts the numeric accuracy of the algorithm, but the optimal set of points for small convolutions remains unknown. Existing work considers only small integers and simple fractions as candidate points. In this work, we propose a novel approach to point selection using points of the form {-1/c , -c, c, 1/c } using the full range of real-valued numbers for c. We show that groups of this form cause cancellations in the Winograd transform matrices that reduce numeric error. We find empirically that the error for different values of c forms a rough curve across the range of real-value numbers helping to localize the values of c that reduce error and that lower errors can be achieved with non-obvious real-valued evaluation points instead of integers or simple fractions. We study a range of sizes for small convolutions and achieve reduction in error ranging from 2% to around 59% for both 1D and 2D convolution. Furthermore, we identify patterns in cases when we select a subset of our proposed points which will always lead to a lower error. Finally we implement a complete Winograd convolution layer and use it to run deep convolution neural networks on real datasets and show that our proposed points reduce error, ranging from 22% to 63%.

Low precision logarithmic number systems: Beyond base-2

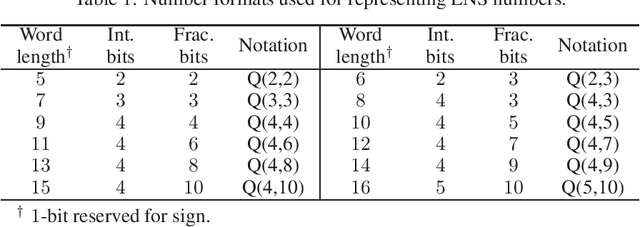
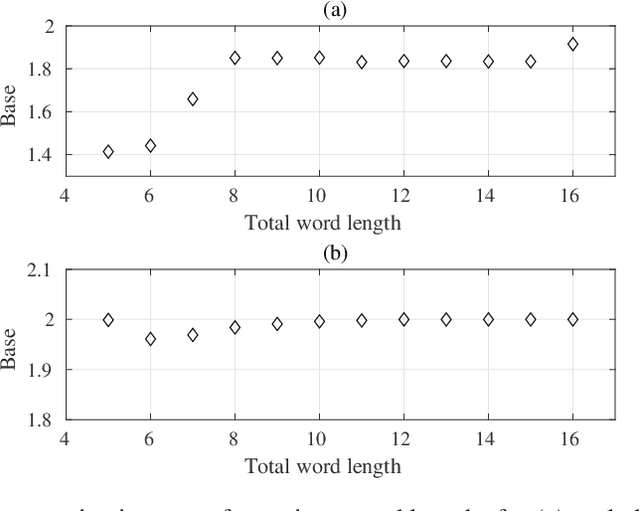
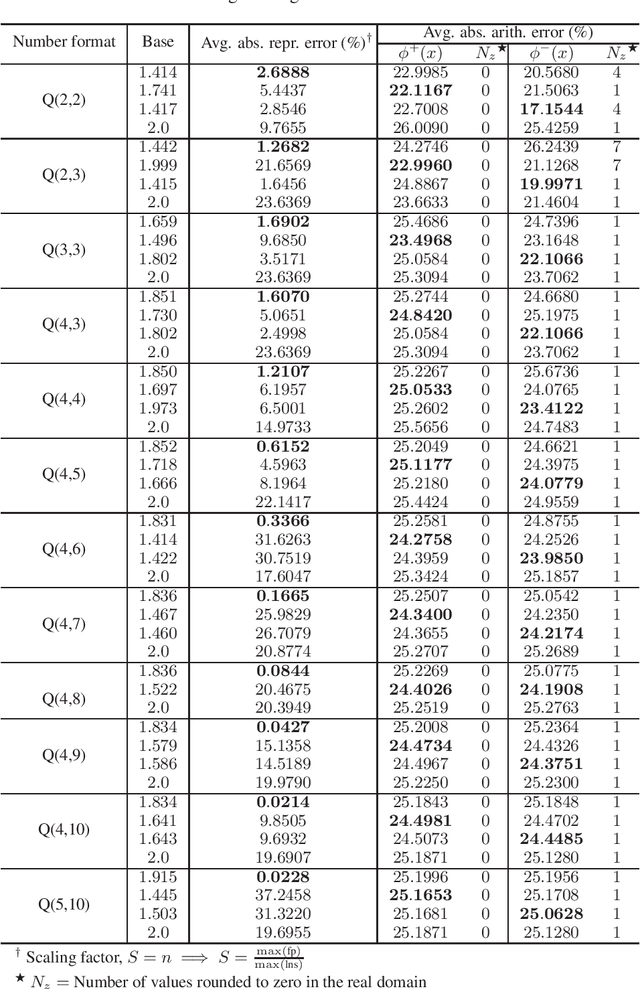
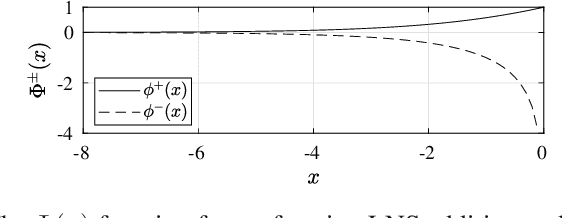
Logarithmic number systems (LNS) are used to represent real numbers in many applications using a constant base raised to a fixed-point exponent making its distribution exponential. This greatly simplifies hardware multiply, divide and square root. LNS with base-2 is most common, but in this paper we show that for low-precision LNS the choice of base has a significant impact. We make four main contributions. First, LNS is not closed under addition and subtraction, so the result is approximate. We show that choosing a suitable base can manipulate the distribution to reduce the average error. Second, we show that low-precision LNS addition and subtraction can be implemented efficiently in logic rather than commonly used ROM lookup tables, the complexity of which can be reduced by an appropriate choice of base. A similar effect is shown where the result of arithmetic has greater precision than the input. Third, where input data from external sources is not expected to be in LNS, we can reduce the conversion error by selecting a LNS base to match the expected distribution of the input. Thus, there is no one base which gives the global optimum, and base selection is a trade-off between different factors. Fourth, we show that circuits realized in LNS require lower area and power consumption for short word lengths.