David Gregg
Bayesian-LoRA: Probabilistic Low-Rank Adaptation of Large Language Models
Jan 28, 2026Abstract:Large Language Models usually put more emphasis on accuracy and therefore, will guess even when not certain about the prediction, which is especially severe when fine-tuned on small datasets due to the inherent tendency toward miscalibration. In this work, we introduce Bayesian-LoRA, which reformulates the deterministic LoRA update as a probabilistic low-rank representation inspired by Sparse Gaussian Processes. We identify a structural isomorphism between LoRA's factorization and Kronecker-factored SGP posteriors, and show that LoRA emerges as a limiting case when posterior uncertainty collapses. We conduct extensive experiments on various LLM architectures across commonsense reasoning benchmarks. With only approximately 0.42M additional parameters and ${\approx}1.2{\times}$ training cost relative to standard LoRA, Bayesian-LoRA significantly improves calibration across models up to 30B, achieving up to 84% ECE reduction and 76% NLL reduction while maintaining competitive accuracy for both in-distribution and out-of-distribution (OoD) evaluations.
Domino Saliency Metrics: Improving Existing Channel Saliency Metrics with Structural Information
May 04, 2022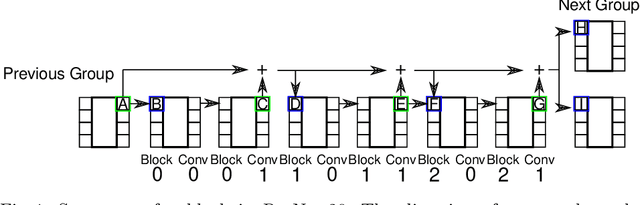
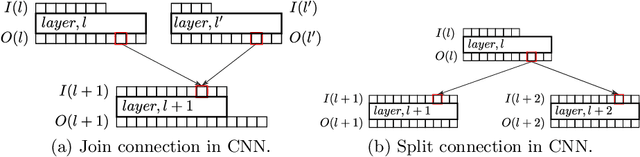
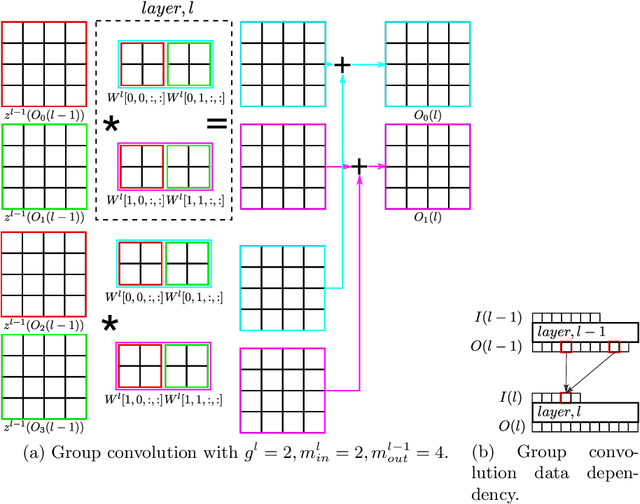
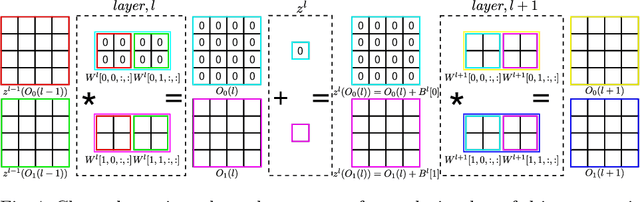
Abstract:Channel pruning is used to reduce the number of weights in a Convolutional Neural Network (CNN). Channel pruning removes slices of the weight tensor so that the convolution layer remains dense. The removal of these weight slices from a single layer causes mismatching number of feature maps between layers of the network. A simple solution is to force the number of feature map between layers to match through the removal of weight slices from subsequent layers. This additional constraint becomes more apparent in DNNs with branches where multiple channels need to be pruned together to keep the network dense. Popular pruning saliency metrics do not factor in the structural dependencies that arise in DNNs with branches. We propose Domino metrics (built on existing channel saliency metrics) to reflect these structural constraints. We test Domino saliency metrics against the baseline channel saliency metrics on multiple networks with branches. Domino saliency metrics improved pruning rates in most tested networks and up to 25% in AlexNet on CIFAR-10.
Winograd Convolution for Deep Neural Networks: Efficient Point Selection
Jan 25, 2022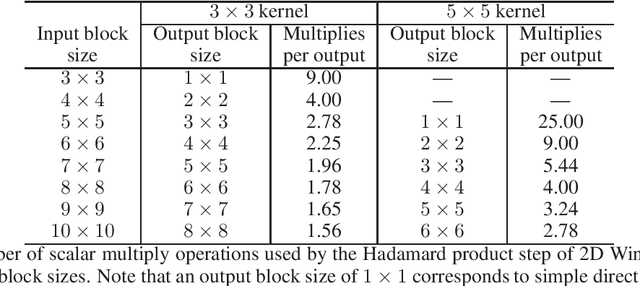
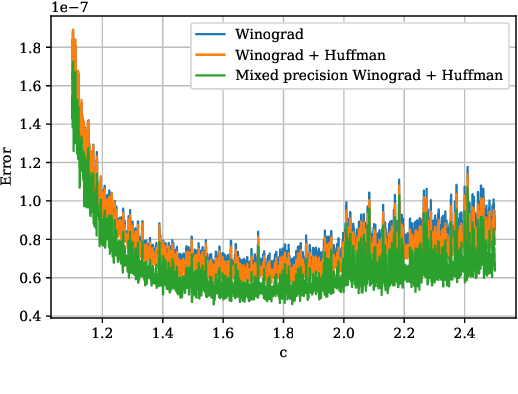
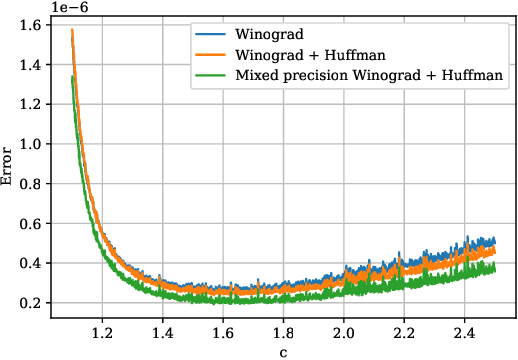

Abstract:Convolutional neural networks (CNNs) have dramatically improved the accuracy of tasks such as object recognition, image segmentation and interactive speech systems. CNNs require large amounts of computing resources because ofcomputationally intensive convolution layers. Fast convolution algorithms such as Winograd convolution can greatly reduce the computational cost of these layers at a cost of poor numeric properties, such that greater savings in computation exponentially increase floating point errors. A defining feature of each Winograd convolution algorithm is a set of real-value points where polynomials are sampled. The choice of points impacts the numeric accuracy of the algorithm, but the optimal set of points for small convolutions remains unknown. Existing work considers only small integers and simple fractions as candidate points. In this work, we propose a novel approach to point selection using points of the form {-1/c , -c, c, 1/c } using the full range of real-valued numbers for c. We show that groups of this form cause cancellations in the Winograd transform matrices that reduce numeric error. We find empirically that the error for different values of c forms a rough curve across the range of real-value numbers helping to localize the values of c that reduce error and that lower errors can be achieved with non-obvious real-valued evaluation points instead of integers or simple fractions. We study a range of sizes for small convolutions and achieve reduction in error ranging from 2% to around 59% for both 1D and 2D convolution. Furthermore, we identify patterns in cases when we select a subset of our proposed points which will always lead to a lower error. Finally we implement a complete Winograd convolution layer and use it to run deep convolution neural networks on real datasets and show that our proposed points reduce error, ranging from 22% to 63%.
Low precision logarithmic number systems: Beyond base-2
Feb 12, 2021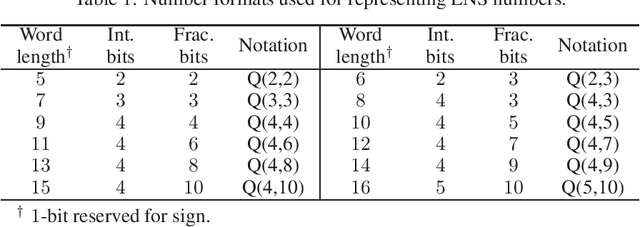
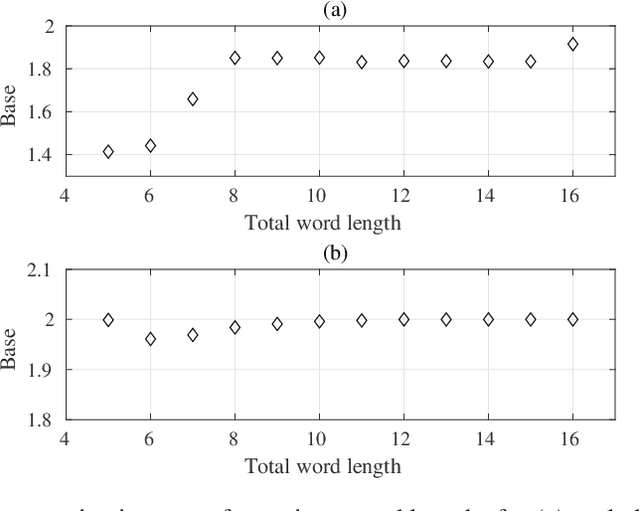
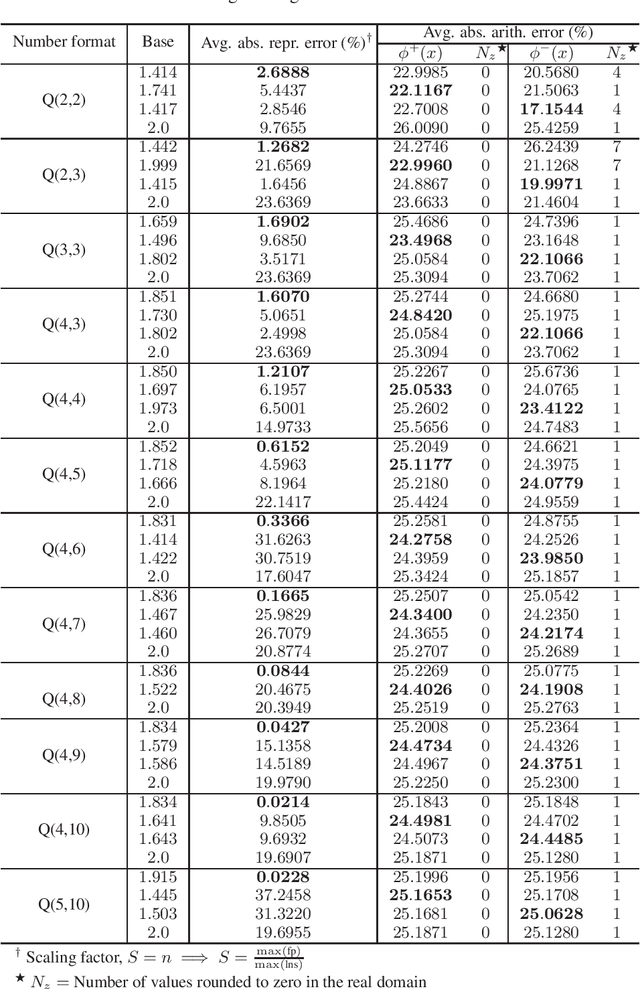
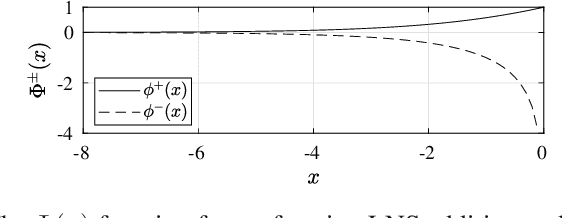
Abstract:Logarithmic number systems (LNS) are used to represent real numbers in many applications using a constant base raised to a fixed-point exponent making its distribution exponential. This greatly simplifies hardware multiply, divide and square root. LNS with base-2 is most common, but in this paper we show that for low-precision LNS the choice of base has a significant impact. We make four main contributions. First, LNS is not closed under addition and subtraction, so the result is approximate. We show that choosing a suitable base can manipulate the distribution to reduce the average error. Second, we show that low-precision LNS addition and subtraction can be implemented efficiently in logic rather than commonly used ROM lookup tables, the complexity of which can be reduced by an appropriate choice of base. A similar effect is shown where the result of arithmetic has greater precision than the input. Third, where input data from external sources is not expected to be in LNS, we can reduce the conversion error by selecting a LNS base to match the expected distribution of the input. Thus, there is no one base which gives the global optimum, and base selection is a trade-off between different factors. Fourth, we show that circuits realized in LNS require lower area and power consumption for short word lengths.
HOBFLOPS CNNs: Hardware Optimized Bitsliced Floating-Point Operations Convolutional Neural Networks
Jul 11, 2020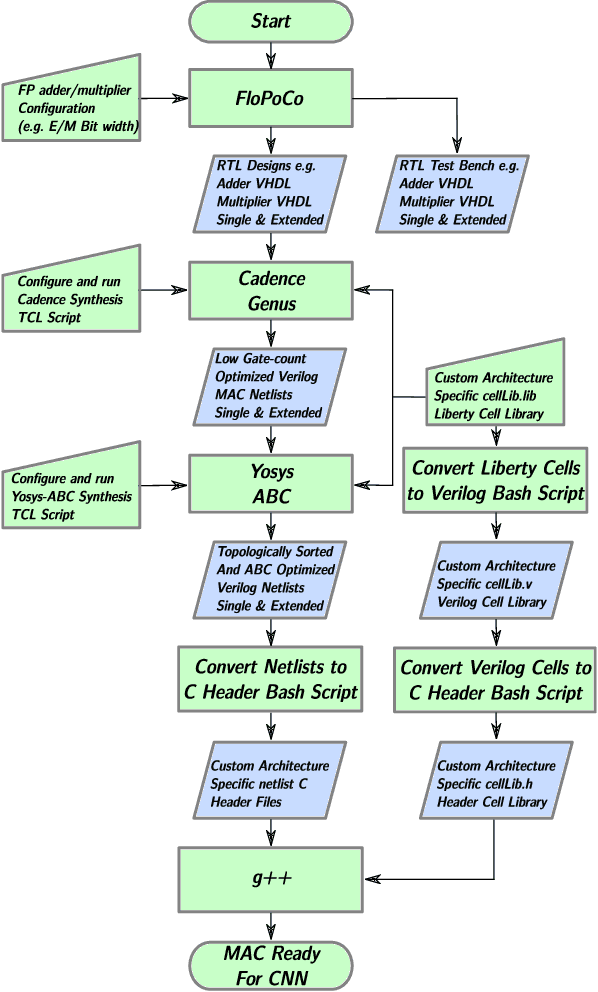

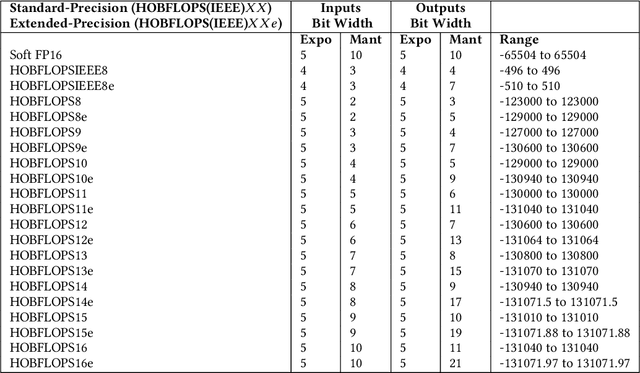
Abstract:Convolutional neural network (CNN) inference is commonly performed with 8-bit integer values. However, higher precision floating-point inference is required. Existing processors support 16- or 32 bit FP but do not typically support custom precision FP. We propose hardware optimized bit-sliced floating-point operators (HOBFLOPS), a method of generating efficient custom-precision emulated bitsliced software FP arithmetic, for CNNs. We compare HOBFLOPS8-HOBFLOPS16 performance against SoftFP16 on Arm Neon and Intel architectures. HOBFLOPS allows researchers to prototype arbitrary-levels of FP arithmetic precision for CNN accelerators. Furthermore, HOBFLOPS fast custom-precision FP CNNs in software may be valuable in cases where memory bandwidth is limited.
Exploiting Weight Redundancy in CNNs: Beyond Pruning and Quantization
Jun 22, 2020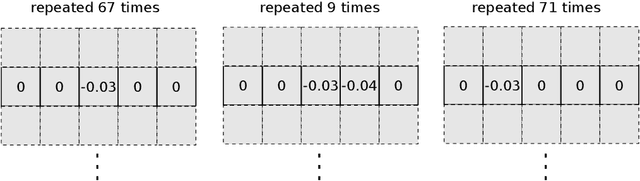
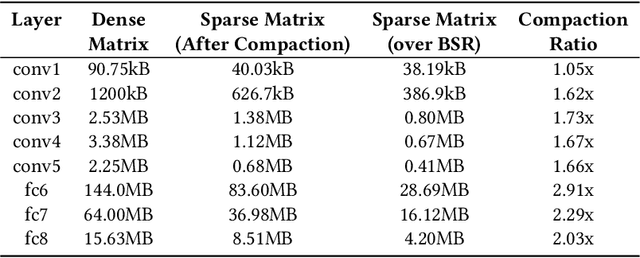
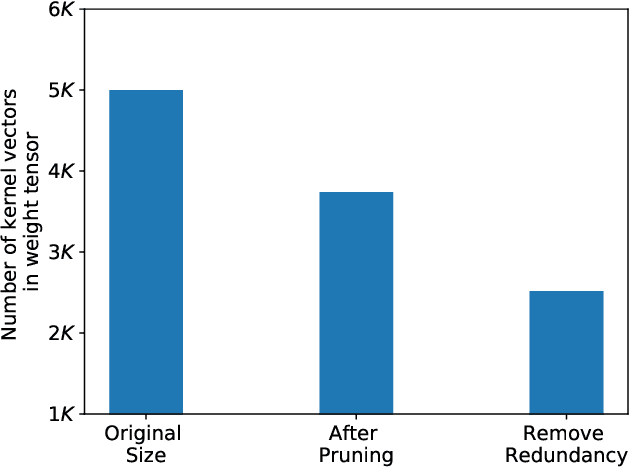
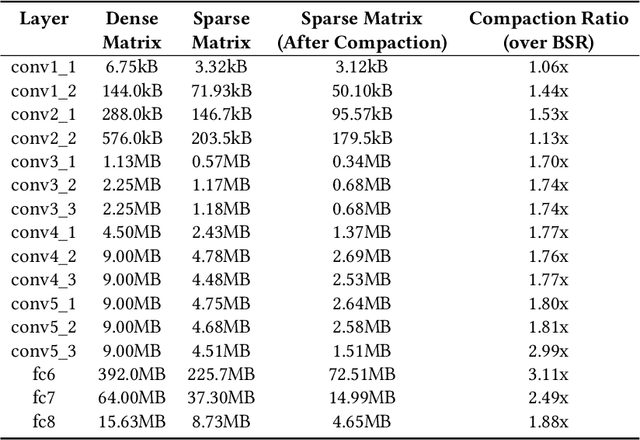
Abstract:Pruning and quantization are proven methods for improving the performance and storage efficiency of convolutional neural networks (CNNs). Pruning removes near-zero weights in tensors and masks weak connections between neurons in neighbouring layers. Quantization reduces the precision of weights by replacing them with numerically similar values that require less storage. In this paper, we identify another form of redundancy in CNN weight tensors, in the form of repeated patterns of similar values. We observe that pruning and quantization both tend to drastically increase the number of repeated patterns in the weight tensors. We investigate several compression schemes to take advantage of this structure in CNN weight data, including multiple forms of Huffman coding, and other approaches inspired by block sparse matrix formats. We evaluate our approach on several well-known CNNs and find that we can achieve compaction ratios of 1.4x to 3.1x in addition to the saving from pruning and quantization.
TASO: Time and Space Optimization for Memory-Constrained DNN Inference
May 21, 2020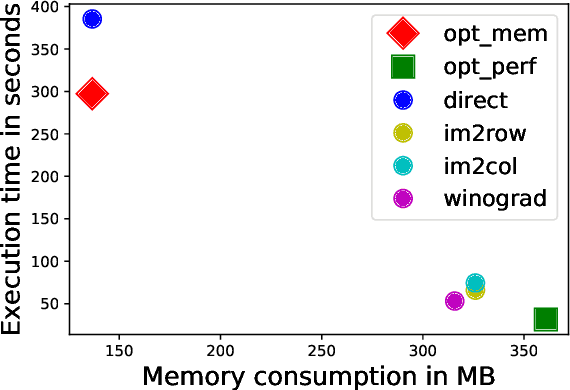
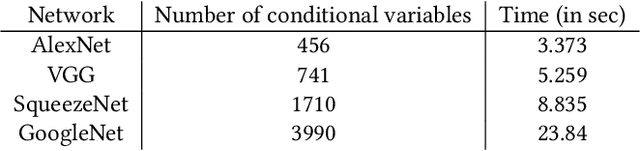

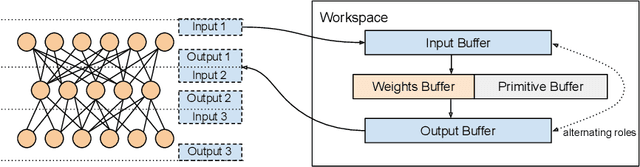
Abstract:Convolutional neural networks (CNNs) are used in many embedded applications, from industrial robotics and automation systems to biometric identification on mobile devices. State-of-the-art classification is typically achieved by large networks, which are prohibitively expensive to run on mobile and embedded devices with tightly constrained memory and energy budgets. We propose an approach for ahead-of-time domain specific optimization of CNN models, based on an integer linear programming (ILP) for selecting primitive operations to implement convolutional layers. We optimize the trade-off between execution time and memory consumption by: 1) attempting to minimize execution time across the whole network by selecting data layouts and primitive operations to implement each layer; and 2) allocating an appropriate workspace that reflects the upper bound of memory footprint per layer. These two optimization strategies can be used to run any CNN on any platform with a C compiler. Our evaluation with a range of popular ImageNet neural architectures (GoogleNet, AlexNet, VGG, ResNet and SqueezeNet) on the ARM Cortex-A15 yields speedups of 8x compared to a greedy algorithm based primitive selection, reduces memory requirement by 2.2x while sacrificing only 15% of inference time compared to a solver that considers inference time only. In addition, our optimization approach exposes a range of optimal points for different configurations across the Pareto frontier of memory and latency trade-off, which can be used under arbitrary system constraints.
Composition of Saliency Metrics for Channel Pruning with a Myopic Oracle
Apr 03, 2020
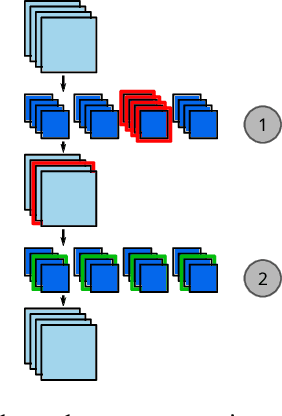

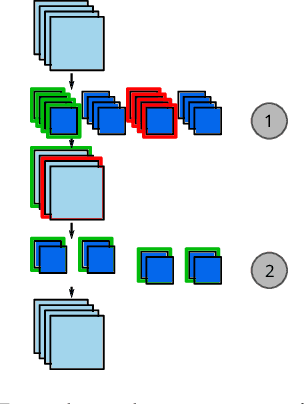
Abstract:The computation and memory needed for Convolutional Neural Network (CNN) inference can be reduced by pruning weights from the trained network. Pruning is guided by a pruning saliency, which heuristically approximates the change in the loss function associated with the removal of specific weights. Many pruning signals have been proposed, but the performance of each heuristic depends on the particular trained network. This leaves the data scientist with a difficult choice. When using any one saliency metric for the entire pruning process, we run the risk of the metric assumptions being invalidated, leading to poor decisions being made by the metric. Ideally we could combine the best aspects of different saliency metrics. However, despite an extensive literature review, we are unable to find any prior work on composing different saliency metrics. The chief difficulty lies in combining the numerical output of different saliency metrics, which are not directly comparable. We propose a method to compose several primitive pruning saliencies, to exploit the cases where each saliency measure does well. Our experiments show that the composition of saliencies avoids many poor pruning choices identified by individual saliencies. In most cases our method finds better selections than even the best individual pruning saliency.
Performance-Oriented Neural Architecture Search
Jan 09, 2020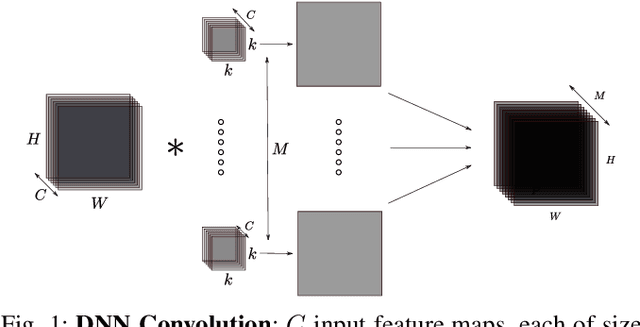
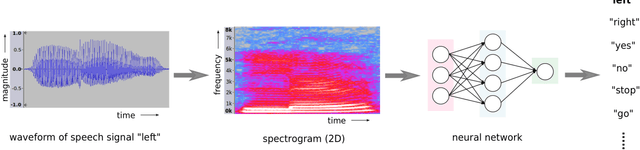

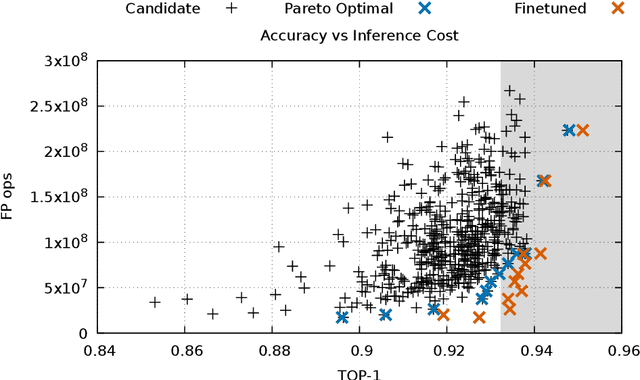
Abstract:Hardware-Software Co-Design is a highly successful strategy for improving performance of domain-specific computing systems. We argue for the application of the same methodology to deep learning; specifically, we propose to extend neural architecture search with information about the hardware to ensure that the model designs produced are highly efficient in addition to the typical criteria around accuracy. Using the task of keyword spotting in audio on edge computing devices, we demonstrate that our approach results in neural architecture that is not only highly accurate, but also efficiently mapped to the computing platform which will perform the inference. Using our modified neural architecture search, we demonstrate $0.88\%$ increase in TOP-1 accuracy with $1.85\times$ reduction in latency for keyword spotting in audio on an embedded SoC, and $1.59\times$ on a high-end GPU.
A Taxonomy of Channel Pruning Signals in CNNs
Jun 11, 2019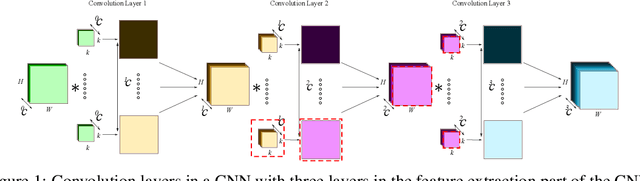


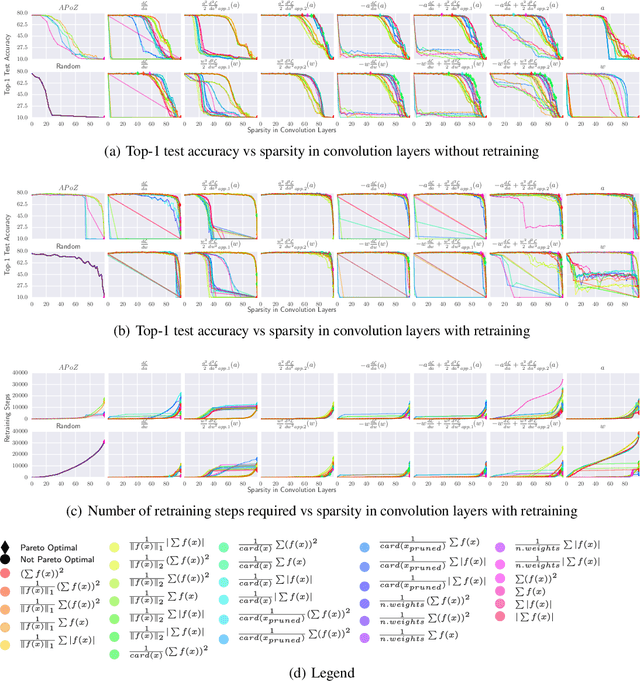
Abstract:Convolutional neural networks (CNNs) are widely used for classification problems. However, they often require large amounts of computation and memory which are not readily available in resource constrained systems. Pruning unimportant parameters from CNNs to reduce these requirements has been a subject of intensive research in recent years. However, novel approaches in pruning signals are sometimes difficult to compare against each other. We propose a taxonomy that classifies pruning signals based on four mostly-orthogonal components of the signal. We also empirically evaluate 396 pruning signals including existing ones, and new signals constructed from the components of existing signals. We find that some of our newly constructed signals outperform the best existing pruning signals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge