An insertable glucose sensor using a compact and cost-effective phosphorescence lifetime imager and machine learning

Optical continuous glucose monitoring (CGM) systems are emerging for personalized glucose management owing to their lower cost and prolonged durability compared to conventional electrochemical CGMs. Here, we report a computational CGM system, which integrates a biocompatible phosphorescence-based insertable biosensor and a custom-designed phosphorescence lifetime imager (PLI). This compact and cost-effective PLI is designed to capture phosphorescence lifetime images of an insertable sensor through the skin, where the lifetime of the emitted phosphorescence signal is modulated by the local concentration of glucose. Because this phosphorescence signal has a very long lifetime compared to tissue autofluorescence or excitation leakage processes, it completely bypasses these noise sources by measuring the sensor emission over several tens of microseconds after the excitation light is turned off. The lifetime images acquired through the skin are processed by neural network-based models for misalignment-tolerant inference of glucose levels, accurately revealing normal, low (hypoglycemia) and high (hyperglycemia) concentration ranges. Using a 1-mm thick skin phantom mimicking the optical properties of human skin, we performed in vitro testing of the PLI using glucose-spiked samples, yielding 88.8% inference accuracy, also showing resilience to random and unknown misalignments within a lateral distance of ~4.7 mm with respect to the position of the insertable sensor underneath the skin phantom. Furthermore, the PLI accurately identified larger lateral misalignments beyond 5 mm, prompting user intervention for re-alignment. The misalignment-resilient glucose concentration inference capability of this compact and cost-effective phosphorescence lifetime imager makes it an appealing wearable diagnostics tool for real-time tracking of glucose and other biomarkers.

The Brain Tumor Segmentation in Pediatrics (BraTS-PEDs) Challenge: Focus on Pediatrics (CBTN-CONNECT-DIPGR-ASNR-MICCAI BraTS-PEDs)

Pediatric tumors of the central nervous system are the most common cause of cancer-related death in children. The five-year survival rate for high-grade gliomas in children is less than 20%. Due to their rarity, the diagnosis of these entities is often delayed, their treatment is mainly based on historic treatment concepts, and clinical trials require multi-institutional collaborations. Here we present the CBTN-CONNECT-DIPGR-ASNR-MICCAI BraTS-PEDs challenge, focused on pediatric brain tumors with data acquired across multiple international consortia dedicated to pediatric neuro-oncology and clinical trials. The CBTN-CONNECT-DIPGR-ASNR-MICCAI BraTS-PEDs challenge brings together clinicians and AI/imaging scientists to lead to faster development of automated segmentation techniques that could benefit clinical trials, and ultimately the care of children with brain tumors.

Microscaling Data Formats for Deep Learning

Narrow bit-width data formats are key to reducing the computational and storage costs of modern deep learning applications. This paper evaluates Microscaling (MX) data formats that combine a per-block scaling factor with narrow floating-point and integer types for individual elements. MX formats balance the competing needs of hardware efficiency, model accuracy, and user friction. Empirical results on over two dozen benchmarks demonstrate practicality of MX data formats as a drop-in replacement for baseline FP32 for AI inference and training with low user friction. We also show the first instance of training generative language models at sub-8-bit weights, activations, and gradients with minimal accuracy loss and no modifications to the training recipe.

Very Efficient Training of Convolutional Neural Networks using Fast Fourier Transform and Overlap-and-Add

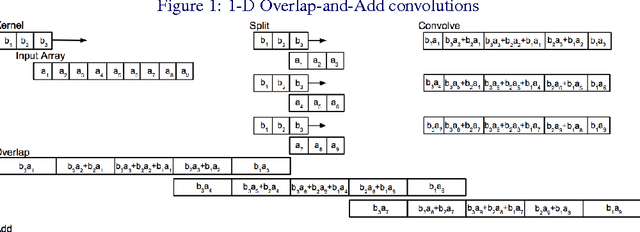
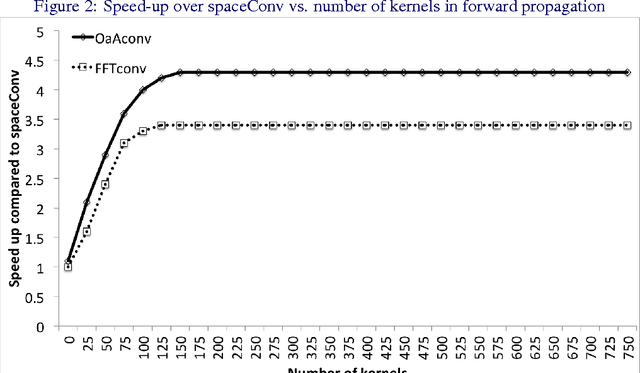
Convolutional neural networks (CNNs) are currently state-of-the-art for various classification tasks, but are computationally expensive. Propagating through the convolutional layers is very slow, as each kernel in each layer must sequentially calculate many dot products for a single forward and backward propagation which equates to $\mathcal{O}(N^{2}n^{2})$ per kernel per layer where the inputs are $N \times N$ arrays and the kernels are $n \times n$ arrays. Convolution can be efficiently performed as a Hadamard product in the frequency domain. The bottleneck is the transformation which has a cost of $\mathcal{O}(N^{2}\log_2 N)$ using the fast Fourier transform (FFT). However, the increase in efficiency is less significant when $N\gg n$ as is the case in CNNs. We mitigate this by using the "overlap-and-add" technique reducing the computational complexity to $\mathcal{O}(N^2\log_2 n)$ per kernel. This method increases the algorithm's efficiency in both the forward and backward propagation, reducing the training and testing time for CNNs. Our empirical results show our method reduces computational time by a factor of up to 16.3 times the traditional convolution implementation for a 8 $\times$ 8 kernel and a 224 $\times$ 224 image.

Zero-Aliasing Correlation Filters for Object Recognition

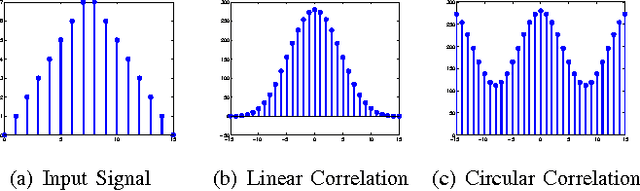
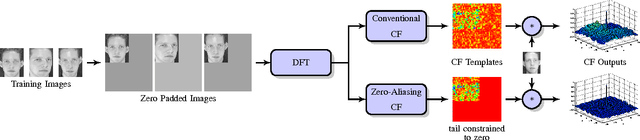
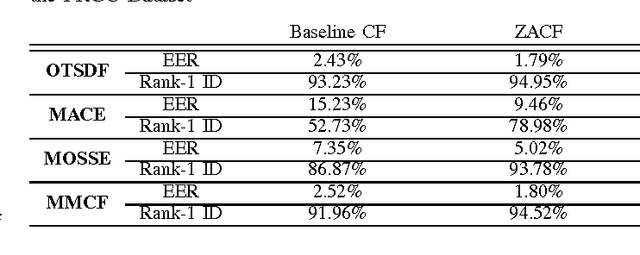
Correlation filters (CFs) are a class of classifiers that are attractive for object localization and tracking applications. Traditionally, CFs have been designed in the frequency domain using the discrete Fourier transform (DFT), where correlation is efficiently implemented. However, existing CF designs do not account for the fact that the multiplication of two DFTs in the frequency domain corresponds to a circular correlation in the time/spatial domain. Because this was previously unaccounted for, prior CF designs are not truly optimal, as their optimization criteria do not accurately quantify their optimization intention. In this paper, we introduce new zero-aliasing constraints that completely eliminate this aliasing problem by ensuring that the optimization criterion for a given CF corresponds to a linear correlation rather than a circular correlation. This means that previous CF designs can be significantly improved by this reformulation. We demonstrate the benefits of this new CF design approach with several important CFs. We present experimental results on diverse data sets and present solutions to the computational challenges associated with computing these CFs. Code for the CFs described in this paper and their respective zero-aliasing versions is available at http://vishnu.boddeti.net/projects/correlation-filters.html