Two-sample Hypothesis Testing for Inhomogeneous Random Graphs

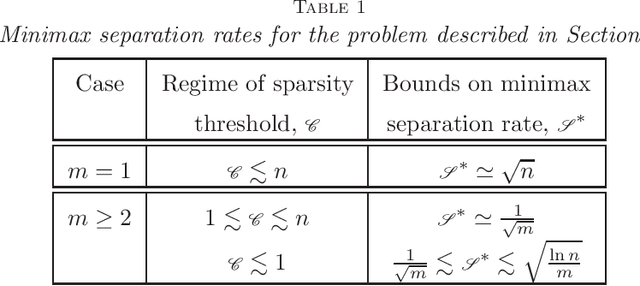
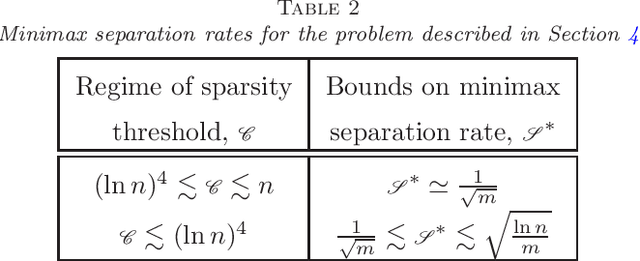
The study of networks leads to a wide range of high dimensional inference problems. In most practical scenarios, one needs to draw inference from a small population of large networks. The present paper studies hypothesis testing of graphs in this high-dimensional regime. We consider the problem of testing between two populations of inhomogeneous random graphs defined on the same set of vertices. We propose tests based on estimates of the Frobenius and operator norms of the difference between the population adjacency matrices. We show that the tests are uniformly consistent in both the "large graph, small sample" and "small graph, large sample" regimes. We further derive lower bounds on the minimax separation rate for the associated testing problems, and show that the constructed tests are near optimal.

Two-Sample Tests for Large Random Graphs Using Network Statistics

We consider a two-sample hypothesis testing problem, where the distributions are defined on the space of undirected graphs, and one has access to only one observation from each model. A motivating example for this problem is comparing the friendship networks on Facebook and LinkedIn. The practical approach to such problems is to compare the networks based on certain network statistics. In this paper, we present a general principle for two-sample hypothesis testing in such scenarios without making any assumption about the network generation process. The main contribution of the paper is a general formulation of the problem based on concentration of network statistics, and consequently, a consistent two-sample test that arises as the natural solution for this problem. We also show that the proposed test is minimax optimal for certain network statistics.

An optimal algorithm for the Thresholding Bandit Problem

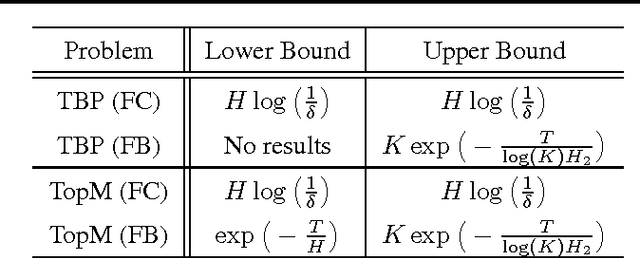
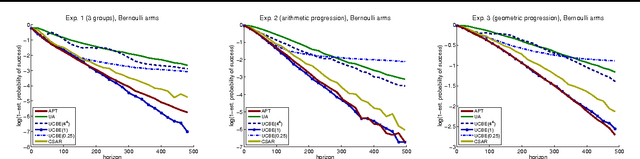
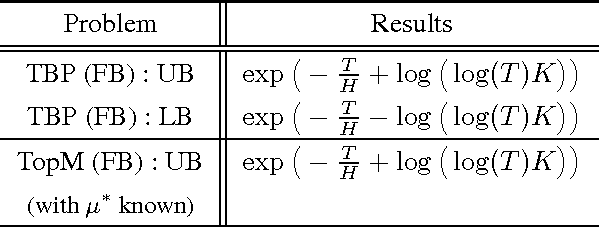
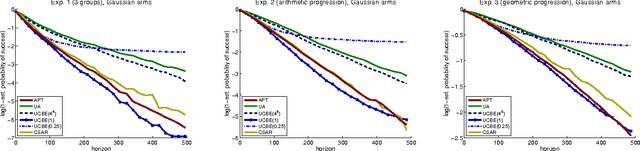
We study a specific \textit{combinatorial pure exploration stochastic bandit problem} where the learner aims at finding the set of arms whose means are above a given threshold, up to a given precision, and \textit{for a fixed time horizon}. We propose a parameter-free algorithm based on an original heuristic, and prove that it is optimal for this problem by deriving matching upper and lower bounds. To the best of our knowledge, this is the first non-trivial pure exploration setting with \textit{fixed budget} for which optimal strategies are constructed.