Multilayer Spectral Graph Clustering via Convex Layer Aggregation: Theory and Algorithms

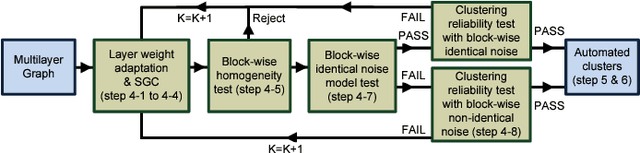
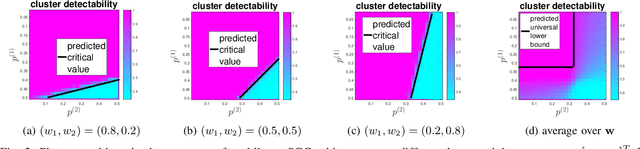
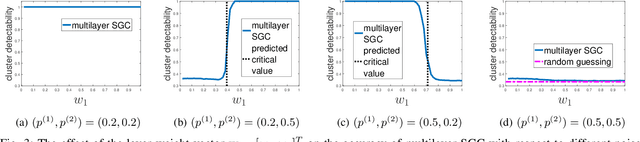
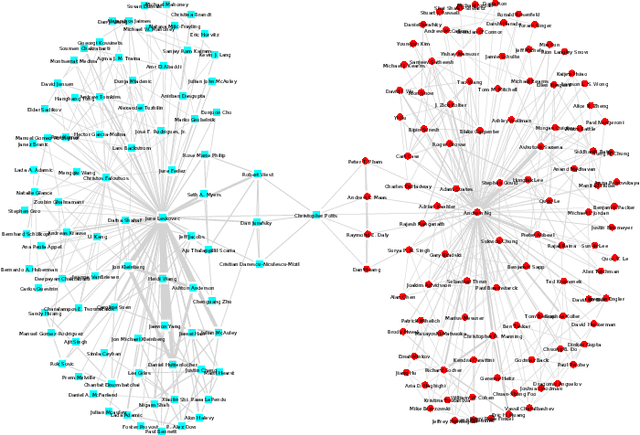
Multilayer graphs are commonly used for representing different relations between entities and handling heterogeneous data processing tasks. Non-standard multilayer graph clustering methods are needed for assigning clusters to a common multilayer node set and for combining information from each layer. This paper presents a multilayer spectral graph clustering (SGC) framework that performs convex layer aggregation. Under a multilayer signal plus noise model, we provide a phase transition analysis of clustering reliability. Moreover, we use the phase transition criterion to propose a multilayer iterative model order selection algorithm (MIMOSA) for multilayer SGC, which features automated cluster assignment and layer weight adaptation, and provides statistical clustering reliability guarantees. Numerical simulations on synthetic multilayer graphs verify the phase transition analysis, and experiments on real-world multilayer graphs show that MIMOSA is competitive or better than other clustering methods.

Robust training on approximated minimal-entropy set

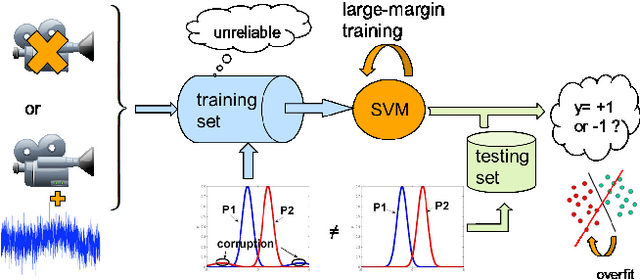
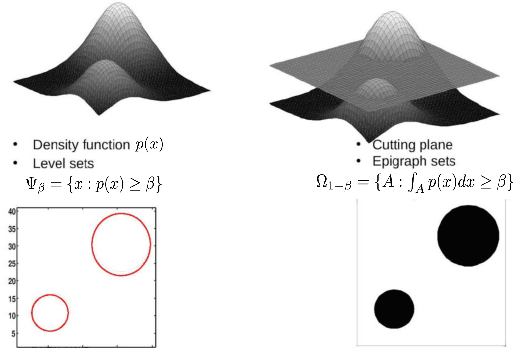
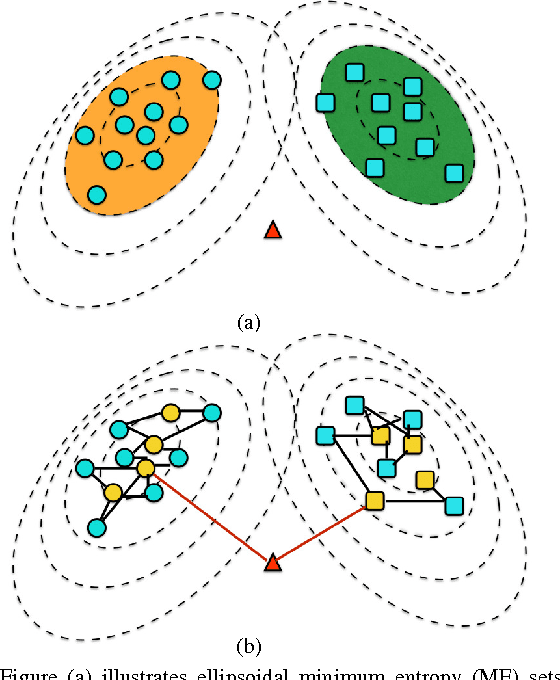
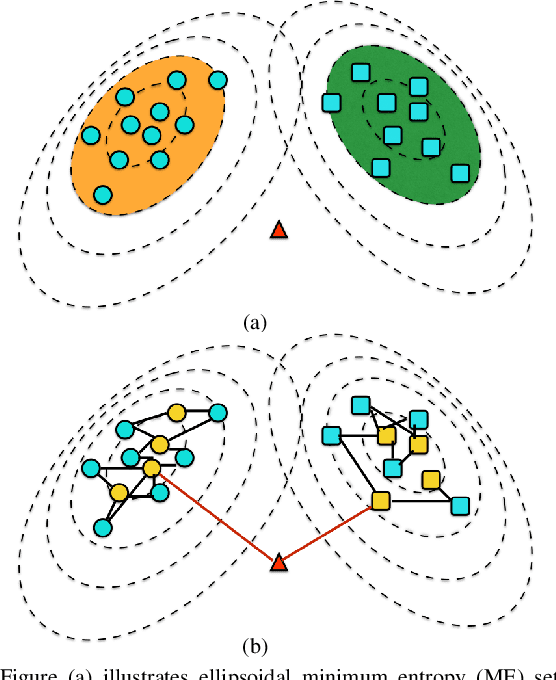
In this paper, we propose a general framework to learn a robust large-margin binary classifier when corrupt measurements, called anomalies, caused by sensor failure might be present in the training set. The goal is to minimize the generalization error of the classifier on non-corrupted measurements while controlling the false alarm rate associated with anomalous samples. By incorporating a non-parametric regularizer based on an empirical entropy estimator, we propose a Geometric-Entropy-Minimization regularized Maximum Entropy Discrimination (GEM-MED) method to learn to classify and detect anomalies in a joint manner. We demonstrate using simulated data and a real multimodal data set. Our GEM-MED method can yield improved performance over previous robust classification methods in terms of both classification accuracy and anomaly detection rate.

Incremental Method for Spectral Clustering of Increasing Orders

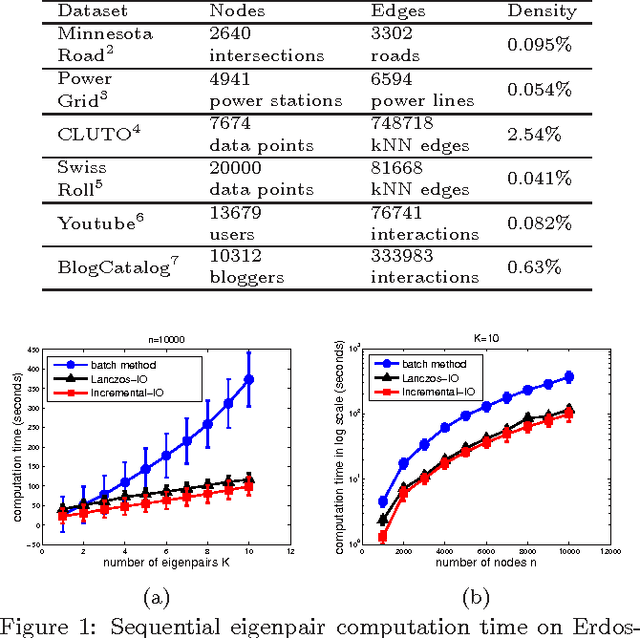
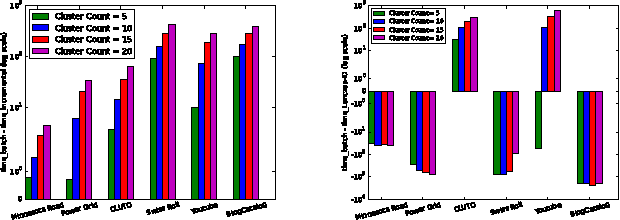
The smallest eigenvalues and the associated eigenvectors (i.e., eigenpairs) of a graph Laplacian matrix have been widely used for spectral clustering and community detection. However, in real-life applications the number of clusters or communities (say, $K$) is generally unknown a-priori. Consequently, the majority of the existing methods either choose $K$ heuristically or they repeat the clustering method with different choices of $K$ and accept the best clustering result. The first option, more often, yields suboptimal result, while the second option is computationally expensive. In this work, we propose an incremental method for constructing the eigenspectrum of the graph Laplacian matrix. This method leverages the eigenstructure of graph Laplacian matrix to obtain the $K$-th eigenpairs of the Laplacian matrix given a collection of all the $K-1$ smallest eigenpairs. Our proposed method adapts the Laplacian matrix such that the batch eigenvalue decomposition problem transforms into an efficient sequential leading eigenpair computation problem. As a practical application, we consider user-guided spectral clustering. Specifically, we demonstrate that users can utilize the proposed incremental method for effective eigenpair computation and determining the desired number of clusters based on multiple clustering metrics.

Multi-centrality Graph Spectral Decompositions and their Application to Cyber Intrusion Detection

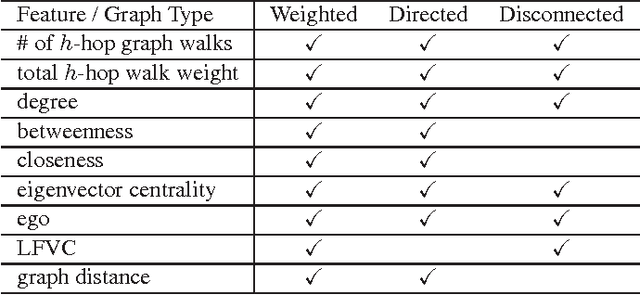
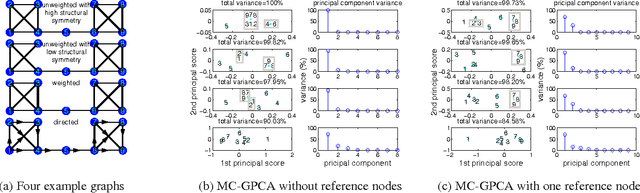
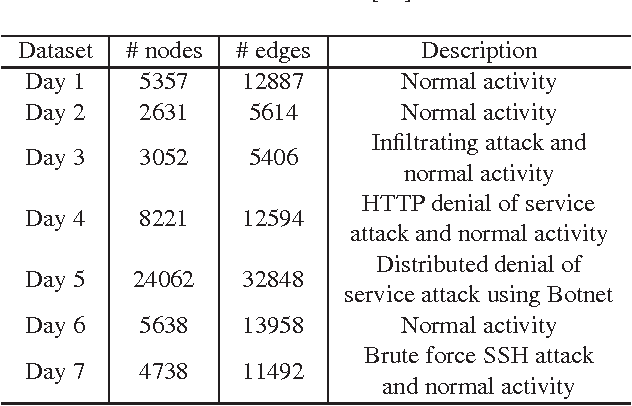
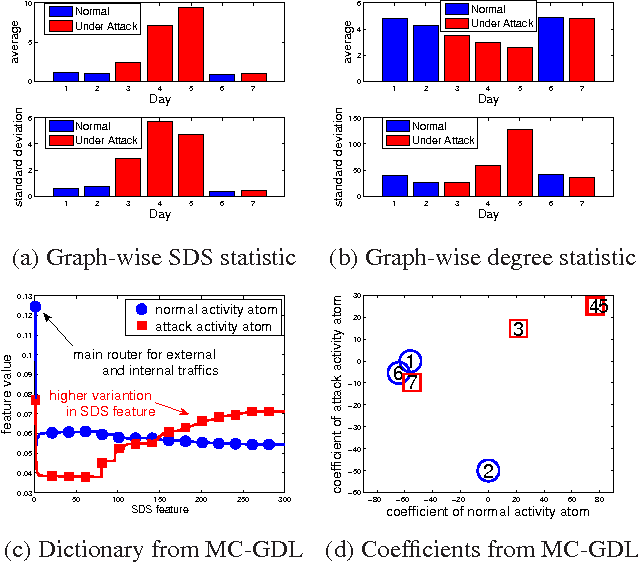
Many modern datasets can be represented as graphs and hence spectral decompositions such as graph principal component analysis (PCA) can be useful. Distinct from previous graph decomposition approaches based on subspace projection of a single topological feature, e.g., the Fiedler vector of centered graph adjacency matrix (graph Laplacian), we propose spectral decomposition approaches to graph PCA and graph dictionary learning that integrate multiple features, including graph walk statistics, centrality measures and graph distances to reference nodes. In this paper we propose a new PCA method for single graph analysis, called multi-centrality graph PCA (MC-GPCA), and a new dictionary learning method for ensembles of graphs, called multi-centrality graph dictionary learning (MC-GDL), both based on spectral decomposition of multi-centrality matrices. As an application to cyber intrusion detection, MC-GPCA can be an effective indicator of anomalous connectivity pattern and MC-GDL can provide discriminative basis for attack classification.

Learning to classify with possible sensor failures

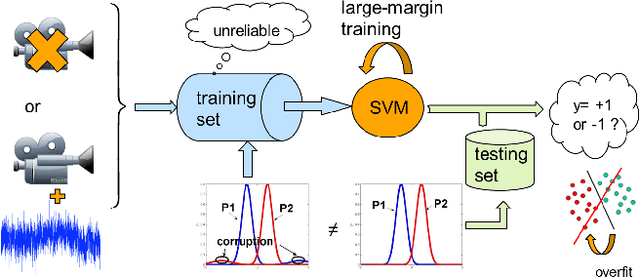
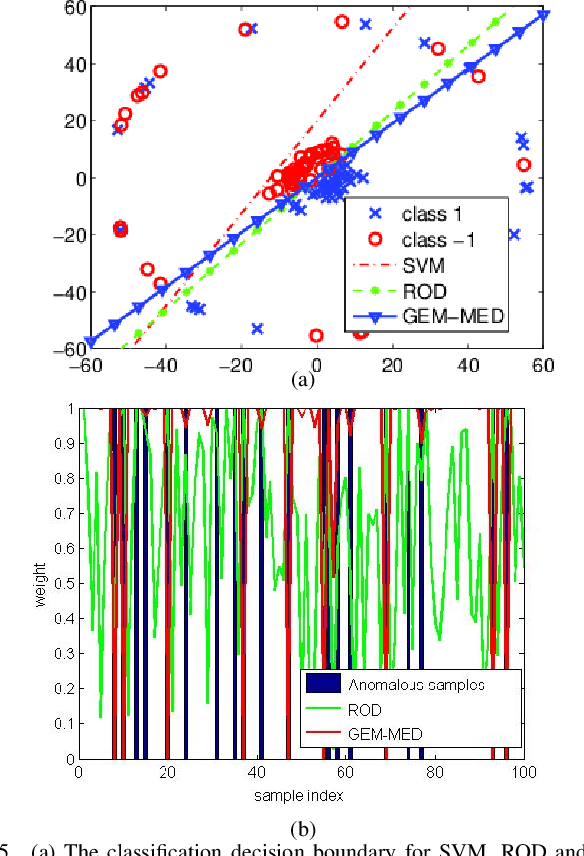
In this paper, we propose a general framework to learn a robust large-margin binary classifier when corrupt measurements, called anomalies, caused by sensor failure might be present in the training set. The goal is to minimize the generalization error of the classifier on non-corrupted measurements while controlling the false alarm rate associated with anomalous samples. By incorporating a non-parametric regularizer based on an empirical entropy estimator, we propose a Geometric-Entropy-Minimization regularized Maximum Entropy Discrimination (GEM-MED) method to learn to classify and detect anomalies in a joint manner. We demonstrate using simulated data and a real multimodal data set. Our GEM-MED method can yield improved performance over previous robust classification methods in terms of both classification accuracy and anomaly detection rate.

Foundational principles for large scale inference: Illustrations through correlation mining

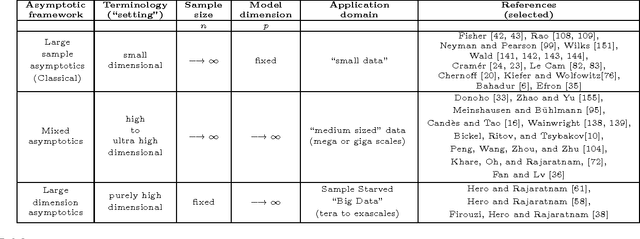
When can reliable inference be drawn in the "Big Data" context? This paper presents a framework for answering this fundamental question in the context of correlation mining, with implications for general large scale inference. In large scale data applications like genomics, connectomics, and eco-informatics the dataset is often variable-rich but sample-starved: a regime where the number $n$ of acquired samples (statistical replicates) is far fewer than the number $p$ of observed variables (genes, neurons, voxels, or chemical constituents). Much of recent work has focused on understanding the computational complexity of proposed methods for "Big Data." Sample complexity however has received relatively less attention, especially in the setting when the sample size $n$ is fixed, and the dimension $p$ grows without bound. To address this gap, we develop a unified statistical framework that explicitly quantifies the sample complexity of various inferential tasks. Sampling regimes can be divided into several categories: 1) the classical asymptotic regime where the variable dimension is fixed and the sample size goes to infinity; 2) the mixed asymptotic regime where both variable dimension and sample size go to infinity at comparable rates; 3) the purely high dimensional asymptotic regime where the variable dimension goes to infinity and the sample size is fixed. Each regime has its niche but only the latter regime applies to exa-scale data dimension. We illustrate this high dimensional framework for the problem of correlation mining, where it is the matrix of pairwise and partial correlations among the variables that are of interest. We demonstrate various regimes of correlation mining based on the unifying perspective of high dimensional learning rates and sample complexity for different structured covariance models and different inference tasks.

A Dictionary Approach to EBSD Indexing

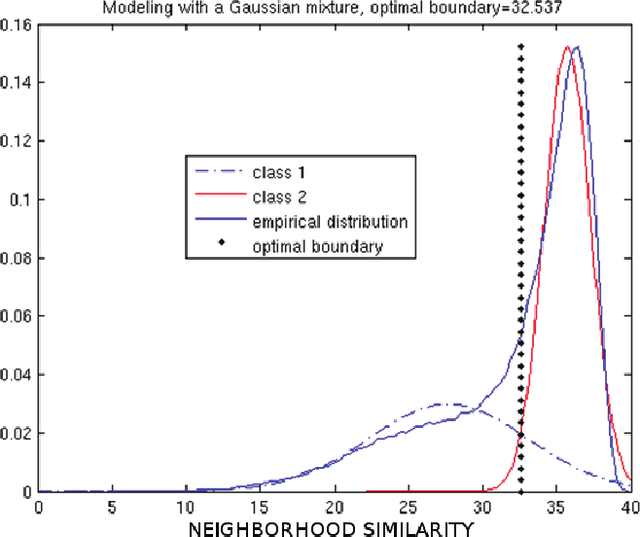
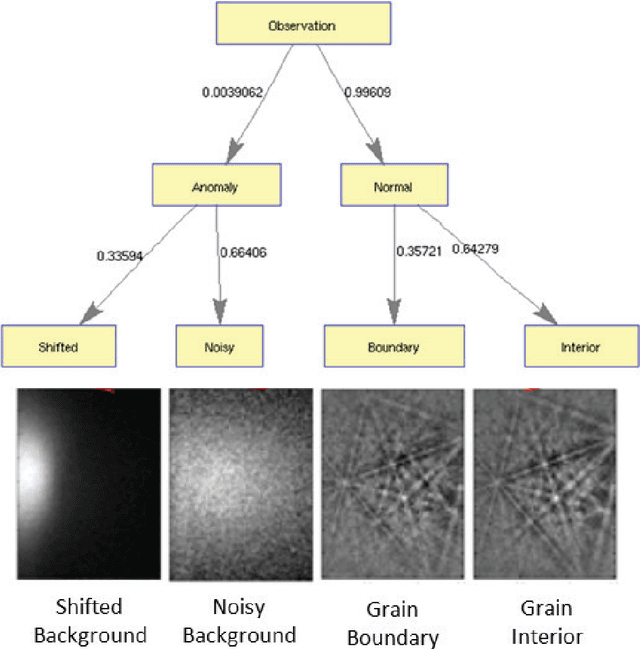
We propose a framework for indexing of grain and sub-grain structures in electron backscatter diffraction (EBSD) images of polycrystalline materials. The framework is based on a previously introduced physics-based forward model by Callahan and De Graef (2013) relating measured patterns to grain orientations (Euler angle). The forward model is tuned to the microscope and the sample symmetry group. We discretize the domain of the forward model onto a dense grid of Euler angles and for each measured pattern we identify the most similar patterns in the dictionary. These patterns are used to identify boundaries, detect anomalies, and index crystal orientations. The statistical distribution of these closest matches is used in an unsupervised binary decision tree (DT) classifier to identify grain boundaries and anomalous regions. The DT classifies a pattern as an anomaly if it has an abnormally low similarity to any pattern in the dictionary. It classifies a pixel as being near a grain boundary if the highly ranked patterns in the dictionary differ significantly over the pixels 3x3 neighborhood. Indexing is accomplished by computing the mean orientation of the closest dictionary matches to each pattern. The mean orientation is estimated using a maximum likelihood approach that models the orientation distribution as a mixture of Von Mises-Fisher distributions over the quaternionic 3-sphere. The proposed dictionary matching approach permits segmentation, anomaly detection, and indexing to be performed in a unified manner with the additional benefit of uncertainty quantification. We demonstrate the proposed dictionary-based approach on a Ni-base IN100 alloy.

Empirically Estimable Classification Bounds Based on a New Divergence Measure

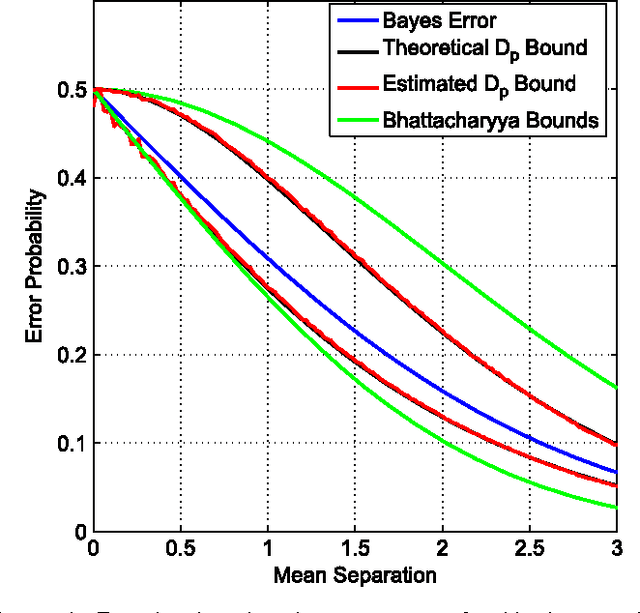
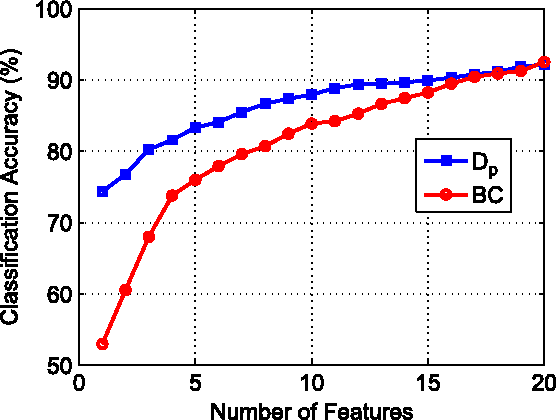
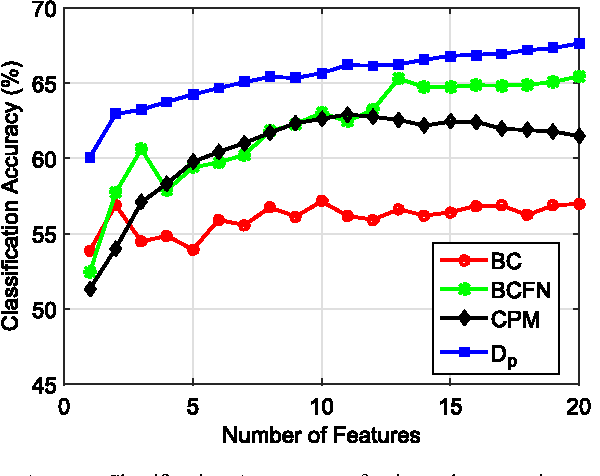
Information divergence functions play a critical role in statistics and information theory. In this paper we show that a non-parametric f-divergence measure can be used to provide improved bounds on the minimum binary classification probability of error for the case when the training and test data are drawn from the same distribution and for the case where there exists some mismatch between training and test distributions. We confirm the theoretical results by designing feature selection algorithms using the criteria from these bounds and by evaluating the algorithms on a series of pathological speech classification tasks.

Empirical non-parametric estimation of the Fisher Information

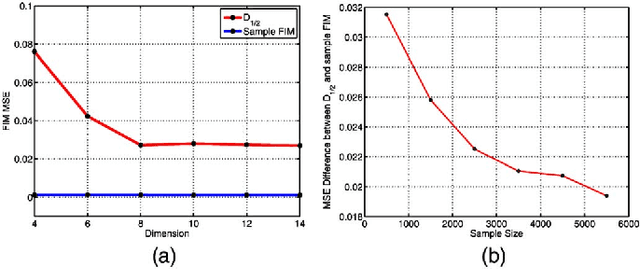
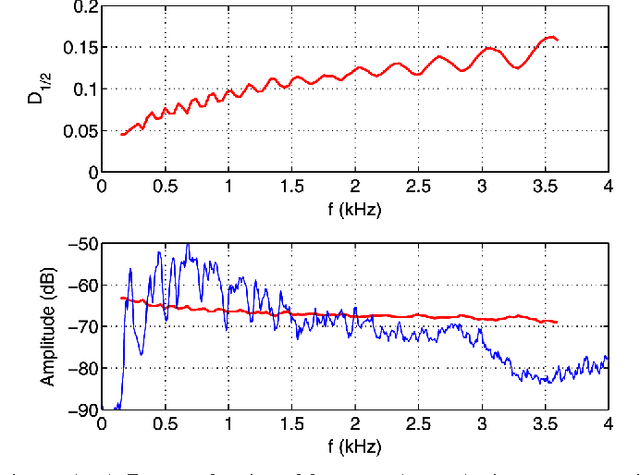
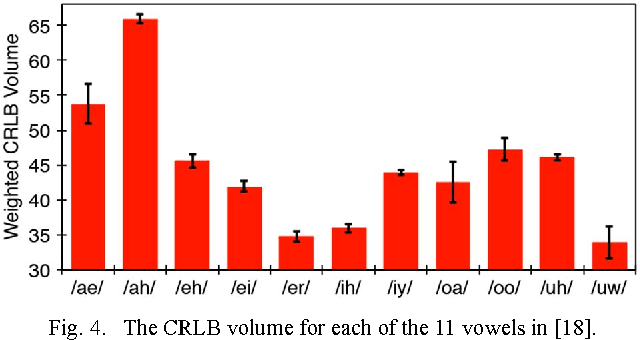
The Fisher information matrix (FIM) is a foundational concept in statistical signal processing. The FIM depends on the probability distribution, assumed to belong to a smooth parametric family. Traditional approaches to estimating the FIM require estimating the probability distribution function (PDF), or its parameters, along with its gradient or Hessian. However, in many practical situations the PDF of the data is not known but the statistician has access to an observation sample for any parameter value. Here we propose a method of estimating the FIM directly from sampled data that does not require knowledge of the underlying PDF. The method is based on non-parametric estimation of an $f$-divergence over a local neighborhood of the parameter space and a relation between curvature of the $f$-divergence and the FIM. Thus we obtain an empirical estimator of the FIM that does not require density estimation and is asymptotically consistent. We empirically evaluate the validity of our approach using two experiments.

Nonlinear unmixing of hyperspectral images: models and algorithms

When considering the problem of unmixing hyperspectral images, most of the literature in the geoscience and image processing areas relies on the widely used linear mixing model (LMM). However, the LMM may be not valid and other nonlinear models need to be considered, for instance, when there are multi-scattering effects or intimate interactions. Consequently, over the last few years, several significant contributions have been proposed to overcome the limitations inherent in the LMM. In this paper, we present an overview of recent advances in nonlinear unmixing modeling.