Mathematical Theory of Collinearity Effects on Machine Learning Variable Importance Measures

In many machine learning problems, understanding variable importance is a central concern. Two common approaches are Permute-and-Predict (PaP), which randomly permutes a feature in a validation set, and Leave-One-Covariate-Out (LOCO), which retrains models after permuting a training feature. Both methods deem a variable important if predictions with the original data substantially outperform those with permutations. In linear regression, empirical studies have linked PaP to regression coefficients and LOCO to $t$-statistics, but a formal theory has been lacking. We derive closed-form expressions for both measures, expressed using square-root transformations. PaP is shown to be proportional to the coefficient and predictor variability: $\text{PaP}_i = \beta_i \sqrt{2\operatorname{Var}(\mathbf{x}^v_i)}$, while LOCO is proportional to the coefficient but dampened by collinearity (captured by $\Delta$): $\text{LOCO}_i = \beta_i (1 -\Delta)\sqrt{1 + c}$. These derivations explain why PaP is largely unaffected by multicollinearity, whereas LOCO is highly sensitive to it. Monte Carlo simulations confirm these findings across varying levels of collinearity. Although derived for linear regression, we also show that these results provide reasonable approximations for models like Random Forests. Overall, this work establishes a theoretical basis for two widely used importance measures, helping analysts understand how they are affected by the true coefficients, dimension, and covariance structure. This work bridges empirical evidence and theory, enhancing the interpretability and application of variable importance measures.

Direct estimation of density functionals using a polynomial basis

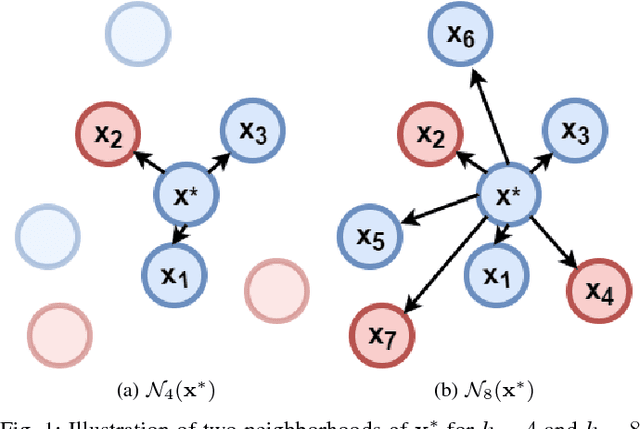
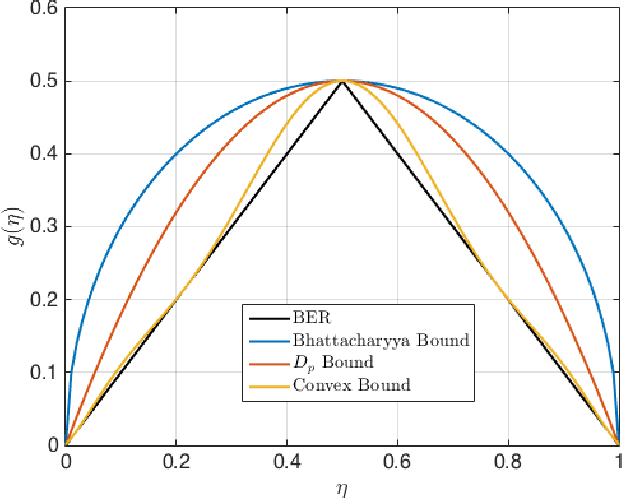
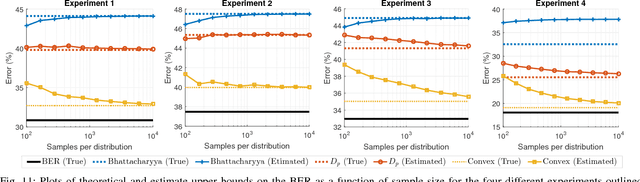
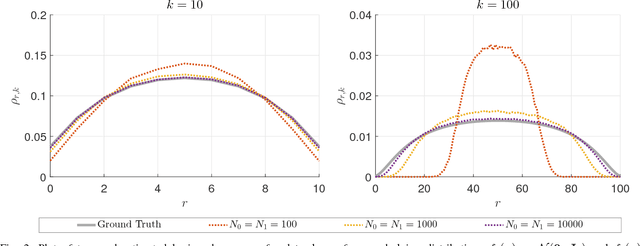
A number of fundamental quantities in statistical signal processing and information theory can be expressed as integral functions of two probability density functions. Such quantities are called density functionals as they map density functions onto the real line. For example, information divergence functions measure the dissimilarity between two probability density functions and are useful in a number of applications. Typically, estimating these quantities requires complete knowledge of the underlying distribution followed by multi-dimensional integration. Existing methods make parametric assumptions about the data distribution or use non-parametric density estimation followed by high-dimensional integration. In this paper, we propose a new alternative. We introduce the concept of "data-driven basis functions" - functions of distributions whose value we can estimate given only samples from the underlying distributions without requiring distribution fitting or direct integration. We derive a new data-driven complete basis that is similar to the deterministic Bernstein polynomial basis and develop two methods for performing basis expansions of functionals of two distributions. We also show that the new basis set allows us to approximate functions of distributions as closely as desired. Finally, we evaluate the methodology by developing data driven estimators for the Kullback-Leibler divergences and the Hellinger distance and by constructing empirical estimates of tight bounds on the Bayes error rate.

Empirically Estimable Classification Bounds Based on a New Divergence Measure

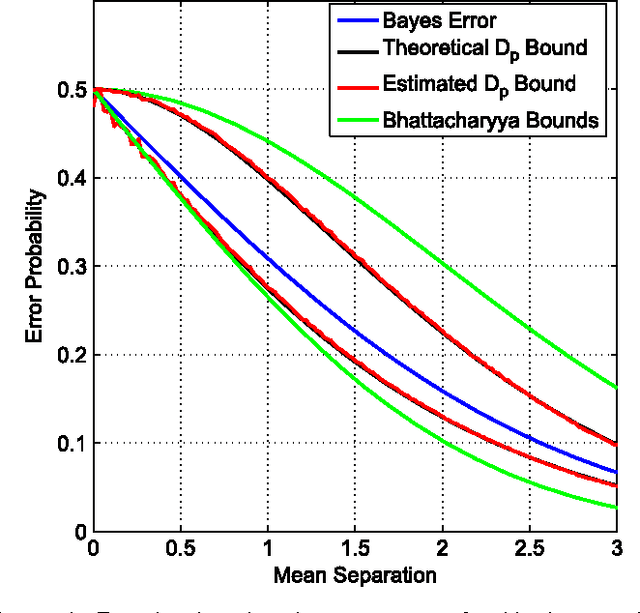
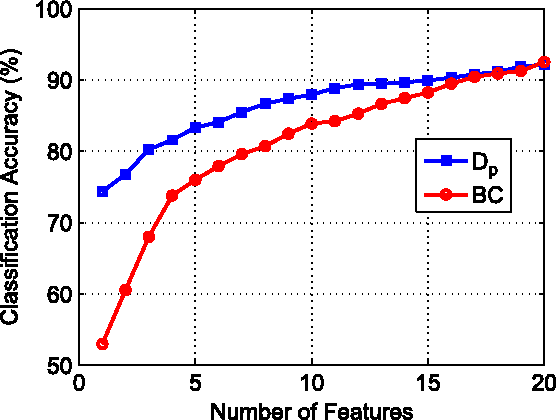
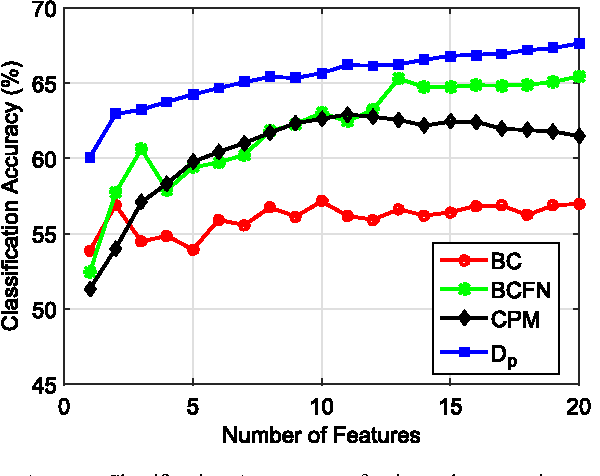
Information divergence functions play a critical role in statistics and information theory. In this paper we show that a non-parametric f-divergence measure can be used to provide improved bounds on the minimum binary classification probability of error for the case when the training and test data are drawn from the same distribution and for the case where there exists some mismatch between training and test distributions. We confirm the theoretical results by designing feature selection algorithms using the criteria from these bounds and by evaluating the algorithms on a series of pathological speech classification tasks.