A Bregman Method for Structure Learning on Sparse Directed Acyclic Graphs

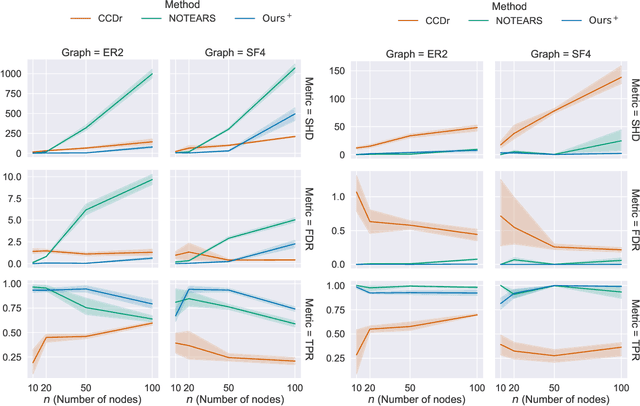
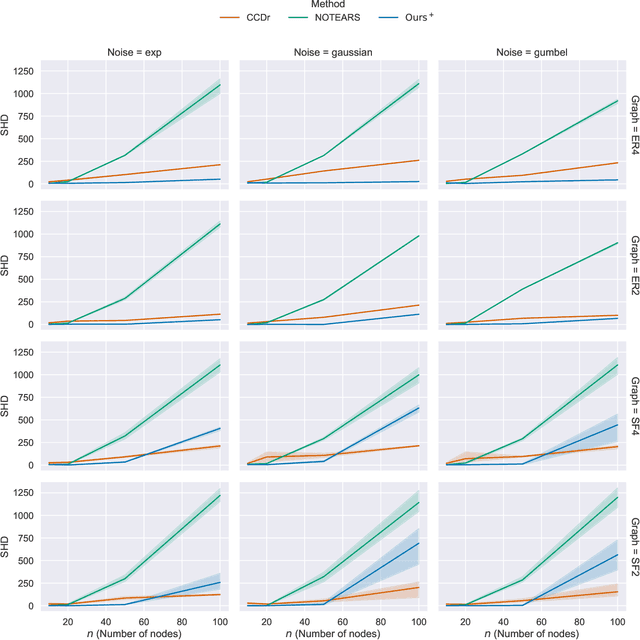
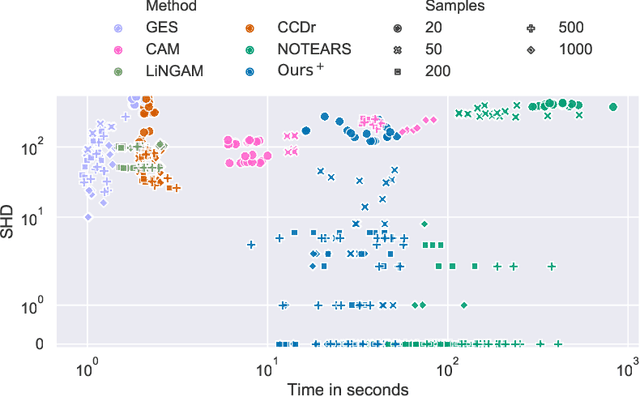
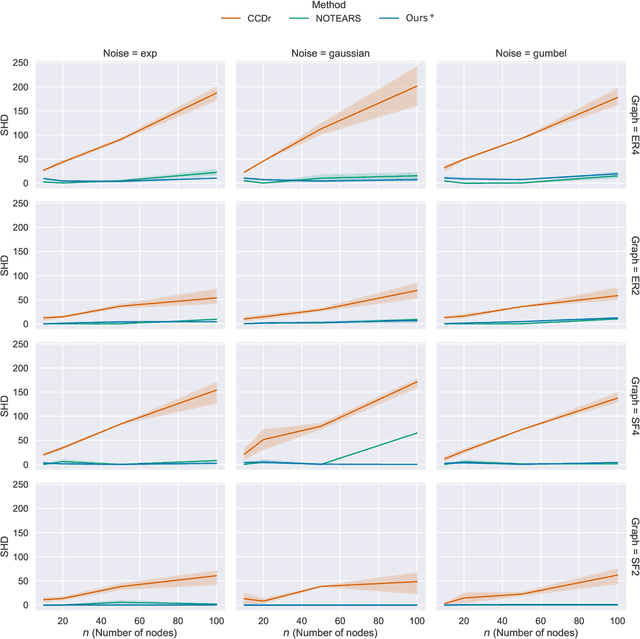
We develop a Bregman proximal gradient method for structure learning on linear structural causal models. While the problem is non-convex, has high curvature and is in fact NP-hard, Bregman gradient methods allow us to neutralize at least part of the impact of curvature by measuring smoothness against a highly nonlinear kernel. This allows the method to make longer steps and significantly improves convergence. Each iteration requires solving a Bregman proximal step which is convex and efficiently solvable for our particular choice of kernel. We test our method on various synthetic and real data sets.

Averaging Atmospheric Gas Concentration Data using Wasserstein Barycenters

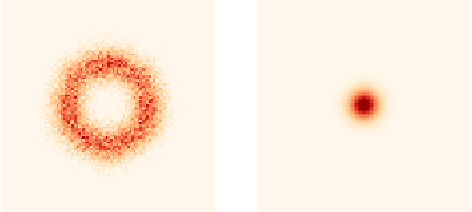
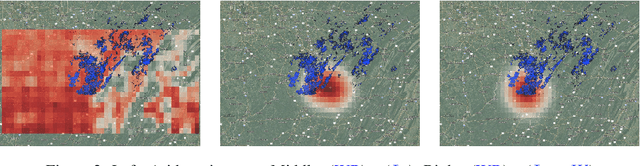
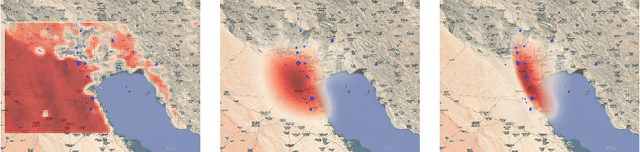
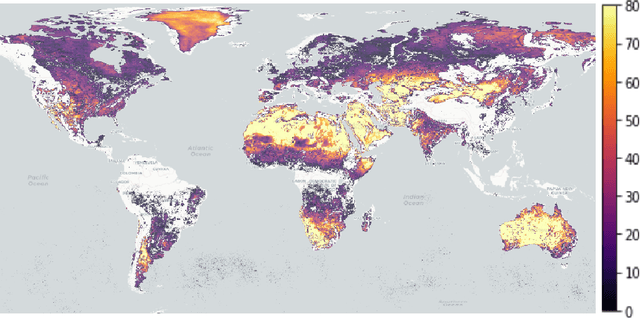
Hyperspectral satellite images report greenhouse gas concentrations worldwide on a daily basis. While taking simple averages of these images over time produces a rough estimate of relative emission rates, atmospheric transport means that simple averages fail to pinpoint the source of these emissions. We propose using Wasserstein barycenters coupled with weather data to average gas concentration data sets and better concentrate the mass around significant sources.

An Optimal Transport Kernel for Feature Aggregation and its Relationship to Attention

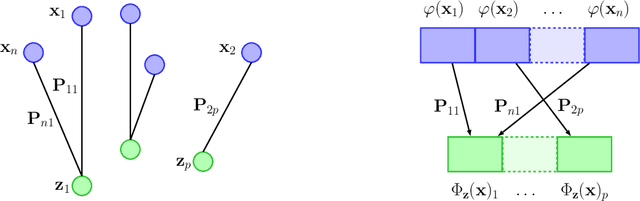
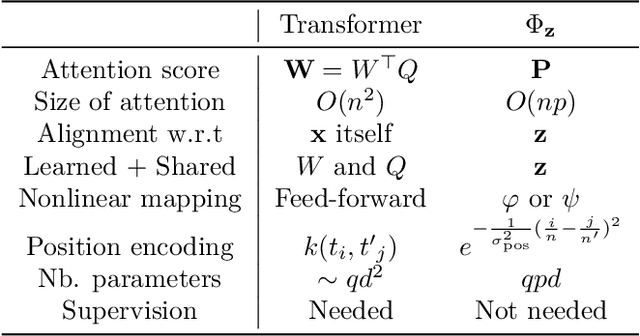
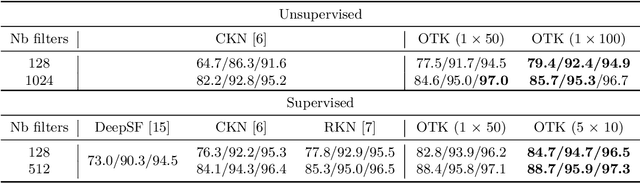
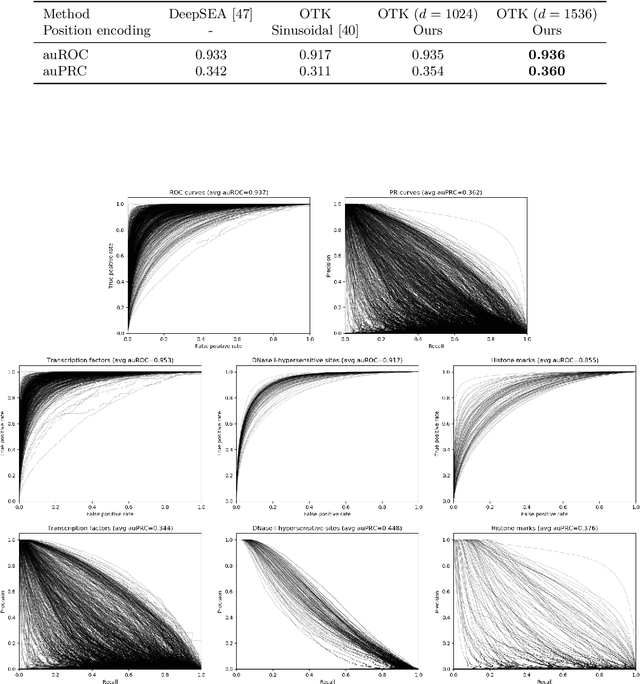
We introduce a kernel for sets of features based on an optimal transport distance, along with an explicit embedding function. Our approach addresses the problem of feature aggregation, or pooling, for sets that exhibit long-range dependencies between their members. More precisely, our embedding aggregates the features of a given set according to the transport plan between the set and a reference shared across the data set. Unlike traditional hand-crafted kernels, our embedding can be optimized for a specific task or data set. It also has a natural connection to attention mechanisms in neural networks, which are commonly used to deal with sets, yet requires less data. Our embedding is particularly suited for biological sequence classification tasks and shows promising results for natural language sequences. We provide an implementation of our embedding that can be used alone or as a module in larger learning models. Our code is freely available at https://github.com/claying/OTK.

FANOK: Knockoffs in Linear Time

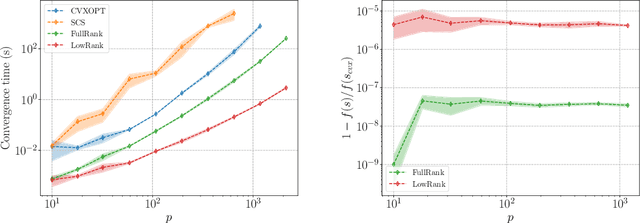
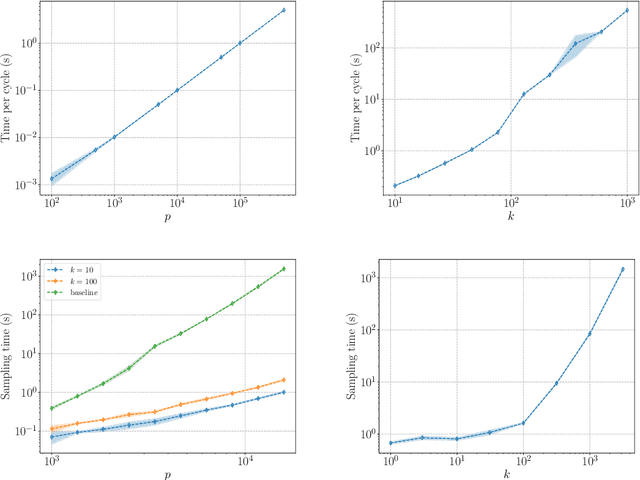
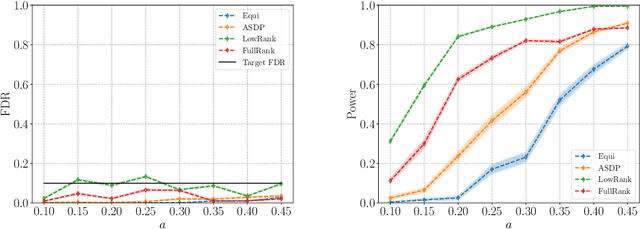
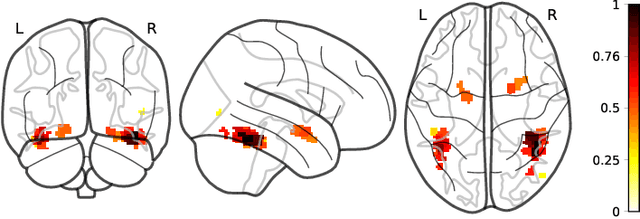
We describe a series of algorithms that efficiently implement Gaussian model-X knockoffs to control the false discovery rate on large scale feature selection problems. Identifying the knockoff distribution requires solving a large scale semidefinite program for which we derive several efficient methods. One handles generic covariance matrices, has a complexity scaling as $O(p^3)$ where $p$ is the ambient dimension, while another assumes a rank $k$ factor model on the covariance matrix to reduce this complexity bound to $O(pk^2)$. We also derive efficient procedures to both estimate factor models and sample knockoff covariates with complexity linear in the dimension. We test our methods on problems with $p$ as large as $500,000$.

Global Convergence of Frank Wolfe on One Hidden Layer Networks

We derive global convergence bounds for the Frank Wolfe algorithm when training one hidden layer neural networks. When using the ReLU activation function, and under tractable preconditioning assumptions on the sample data set, the linear minimization oracle used to incrementally form the solution can be solved explicitly as a second order cone program. The classical Frank Wolfe algorithm then converges with rate $O(1/T)$ where $T$ is both the number of neurons and the number of calls to the oracle.

Complexity Guarantees for Polyak Steps with Momentum

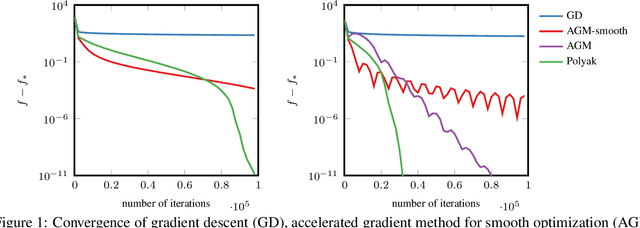
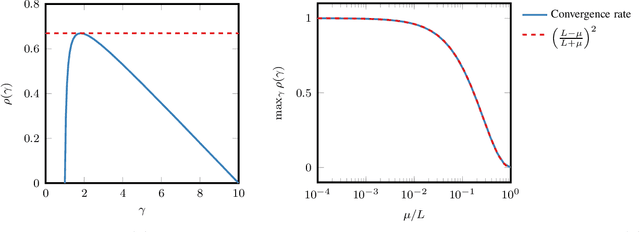
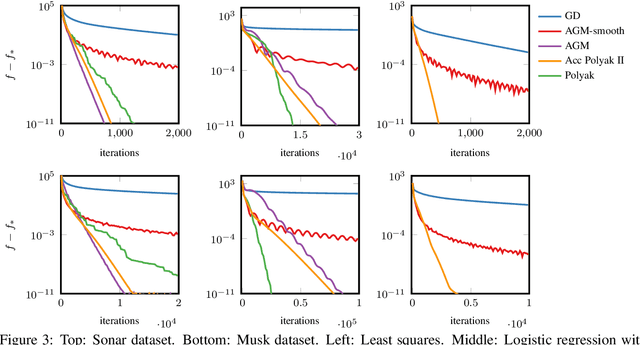
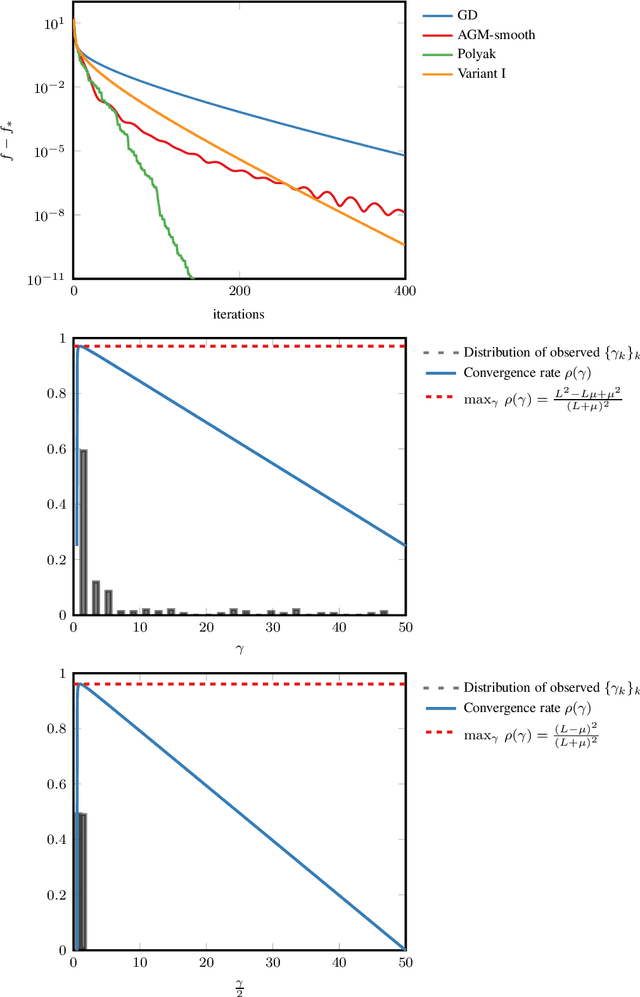
In smooth strongly convex optimization, or in the presence of H\"olderian error bounds, knowledge of the curvature parameter is critical for obtaining simple methods with accelerated rates. In this work, we study a class of methods, based on Polyak steps, where this knowledge is substituted by that of the optimal value, $f_*$. We first show slightly improved convergence bounds than previously known for the classical case of simple gradient descent with Polyak steps, we then derive an accelerated gradient method with Polyak steps and momentum, along with convergence guarantees.

Screening Data Points in Empirical Risk Minimization via Ellipsoidal Regions and Safe Loss Function

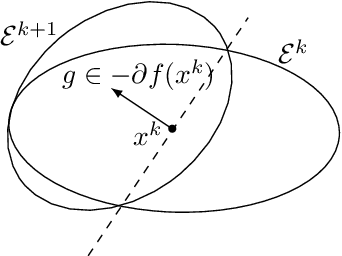
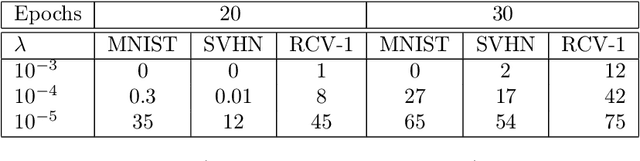
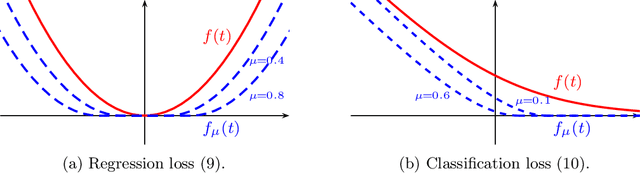
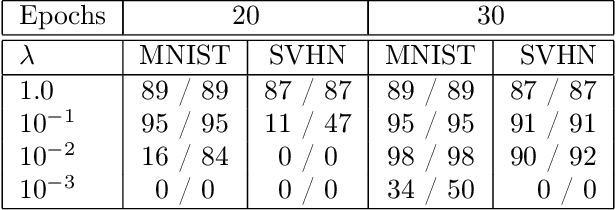
We design simple screening tests to automatically discard data samples in empirical risk minimization without losing optimization guarantees. We derive loss functions that produce dual objectives with a sparse solution. We also show how to regularize convex losses to ensure such a dual sparsity-inducing property, and propose a general method to design screening tests for classification or regression based on ellipsoidal approximations of the optimal set. In addition to producing computational gains, our approach also allows us to compress a dataset into a subset of representative points.

Ranking and synchronization from pairwise measurements via SVD

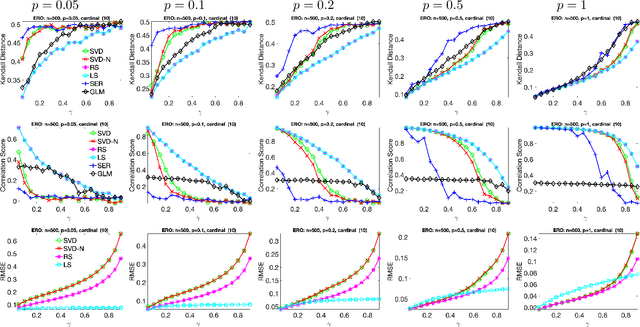
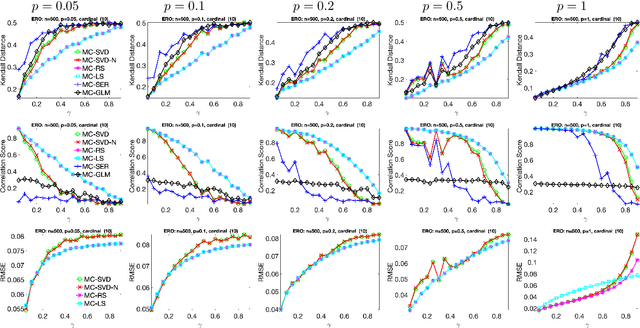
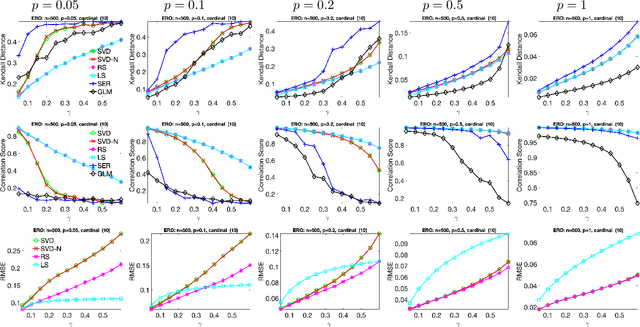
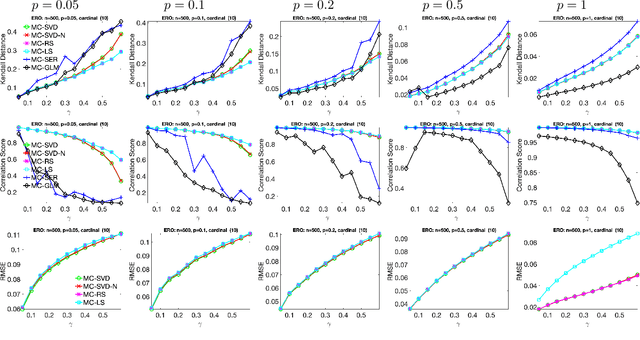
Given a measurement graph $G= (V,E)$ and an unknown signal $r \in \mathbb{R}^n$, we investigate algorithms for recovering $r$ from pairwise measurements of the form $r_i - r_j$; $\{i,j\} \in E$. This problem arises in a variety of applications, such as ranking teams in sports data and time synchronization of distributed networks. Framed in the context of ranking, the task is to recover the ranking of $n$ teams (induced by $r$) given a small subset of noisy pairwise rank offsets. We propose a simple SVD-based algorithmic pipeline for both the problem of time synchronization and ranking. We provide a detailed theoretical analysis in terms of robustness against both sampling sparsity and noise perturbations with outliers, using results from matrix perturbation and random matrix theory. Our theoretical findings are complemented by a detailed set of numerical experiments on both synthetic and real data, showcasing the competitiveness of our proposed algorithms with other state-of-the-art methods.

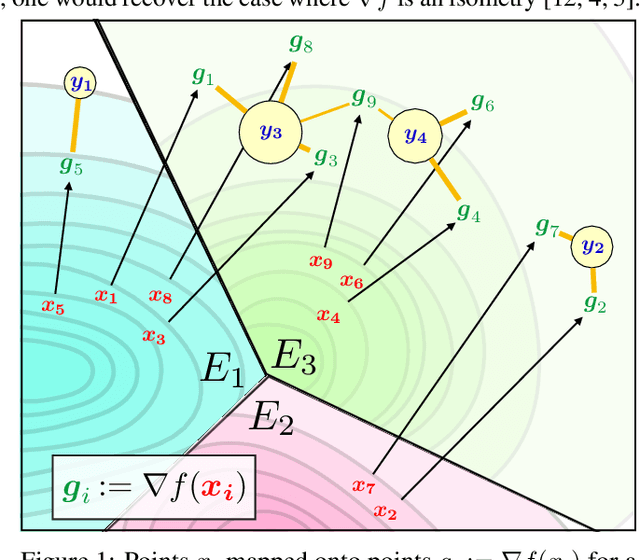
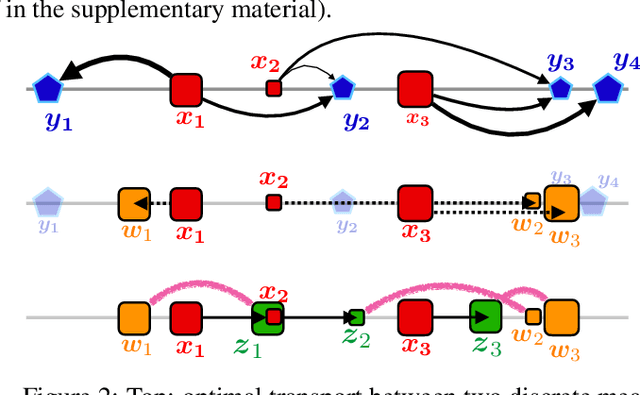
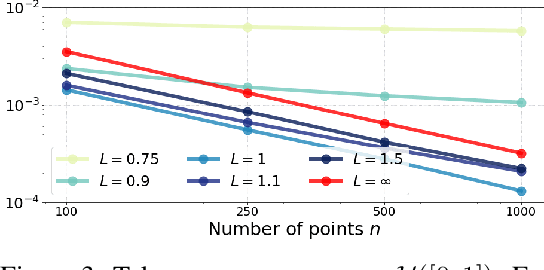
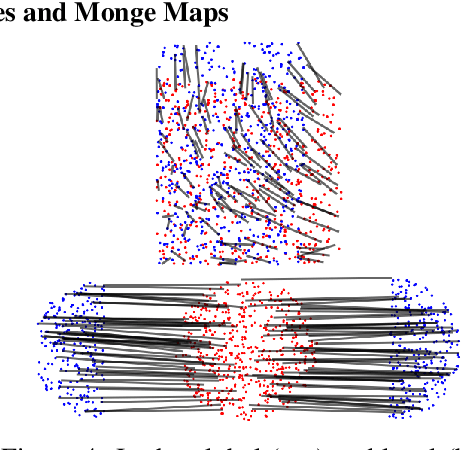
Regularity as Regularization: Smooth and Strongly Convex Brenier Potentials in Optimal Transport

The problem of estimating Wasserstein distances in high-dimensional spaces suffers from the curse of dimensionality: One needs an exponential (w.r.t. dimension) number of samples for the distance between two measures to be comparable to that evaluated using i.i.d samples. Therefore, using the optimal transport (OT) geometry in machine learning involves regularizing it, one way or another. One of the greatest achievements of the OT literature in recent years lies in regularity theory: one can prove under suitable hypothesis that the OT map between two measures is Lipschitz, or, equivalently when studying 2-Wasserstein distances, that the Brenier convex potential (whose gradient yields an optimal map) is a smooth function. We propose in this work to go backwards, and adopt instead regularity as a regularization tool. We propose algorithms working on discrete measures that can recover nearly optimal transport maps that have small distortion, or, equivalently, nearly optimal Brenier potential that are strongly convex and smooth. For univariate measures, we show that computing these potentials is equivalent to solving an isotonic regression problem under Lipschitz and strong monotonicity constraints. For multivariate measures the problem boils down to a non-convex QCQP problem, which can be relaxed to a semidefinite program. Most importantly, we recover as the result of this optimization the values and gradients of the Brenier potential on sampled points, but show how that they can be more generally evaluated on any new point, at the cost of solving a QP for each new evaluation. Building on these two formulations we propose practical algorithms to estimate and evaluate transport maps with desired smoothness/strong convexity properties, illustrate their statistical performance and visualize maps on a color transfer task.

Naive Feature Selection: Sparsity in Naive Bayes

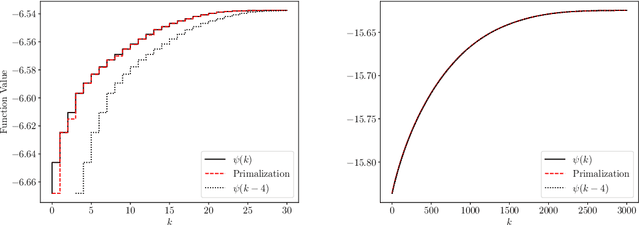
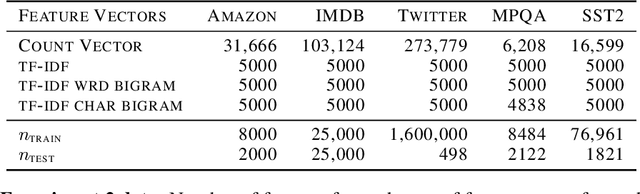
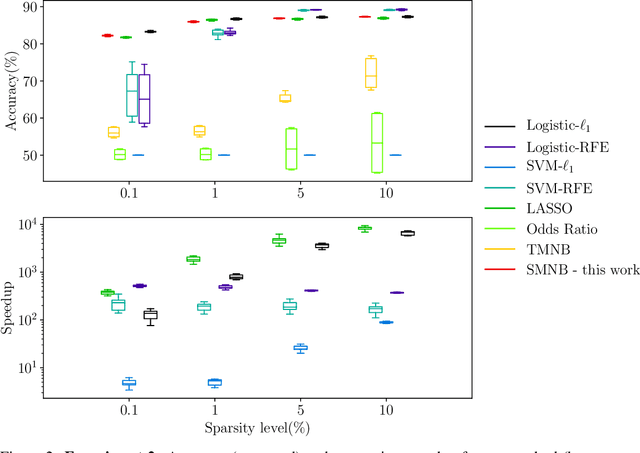
Due to its linear complexity, naive Bayes classification remains an attractive supervised learning method, especially in very large-scale settings. We propose a sparse version of naive Bayes, which can be used for feature selection. This leads to a combinatorial maximum-likelihood problem, for which we provide an exact solution in the case of binary data, or a bound in the multinomial case. We prove that our bound becomes tight as the marginal contribution of additional features decreases. Both binary and multinomial sparse models are solvable in time almost linear in problem size, representing a very small extra relative cost compared to the classical naive Bayes. Numerical experiments on text data show that the naive Bayes feature selection method is as statistically effective as state-of-the-art feature selection methods such as recursive feature elimination, $l_1$-penalized logistic regression and LASSO, while being orders of magnitude faster. For a large data set, having more than with $1.6$ million training points and about $12$ million features, and with a non-optimized CPU implementation, our sparse naive Bayes model can be trained in less than 15 seconds.