Dynamic angular synchronization under smoothness constraints

Given an undirected measurement graph $\mathcal{H} = ([n], \mathcal{E})$, the classical angular synchronization problem consists of recovering unknown angles $\theta_1^*,\dots,\theta_n^*$ from a collection of noisy pairwise measurements of the form $(\theta_i^* - \theta_j^*) \mod 2\pi$, for all $\{i,j\} \in \mathcal{E}$. This problem arises in a variety of applications, including computer vision, time synchronization of distributed networks, and ranking from pairwise comparisons. In this paper, we consider a dynamic version of this problem where the angles, and also the measurement graphs evolve over $T$ time points. Assuming a smoothness condition on the evolution of the latent angles, we derive three algorithms for joint estimation of the angles over all time points. Moreover, for one of the algorithms, we establish non-asymptotic recovery guarantees for the mean-squared error (MSE) under different statistical models. In particular, we show that the MSE converges to zero as $T$ increases under milder conditions than in the static setting. This includes the setting where the measurement graphs are highly sparse and disconnected, and also when the measurement noise is large and can potentially increase with $T$. We complement our theoretical results with experiments on synthetic data.

Joint Learning of Linear Dynamical Systems under Smoothness Constraints

We consider the problem of joint learning of multiple linear dynamical systems. This has received significant attention recently under different types of assumptions on the model parameters. The setting we consider involves a collection of $m$ linear systems each of which resides on a node of a given undirected graph $G = ([m], \mathcal{E})$. We assume that the system matrices are marginally stable, and satisfy a smoothness constraint w.r.t $G$ -- akin to the quadratic variation of a signal on a graph. Given access to the states of the nodes over $T$ time points, we then propose two estimators for joint estimation of the system matrices, along with non-asymptotic error bounds on the mean-squared error (MSE). In particular, we show conditions under which the MSE converges to zero as $m$ increases, typically polynomially fast w.r.t $m$. The results hold under mild (i.e., $T \sim \log m$), or sometimes, even no assumption on $T$ (i.e. $T \geq 2$).

Graph Matching via convex relaxation to the simplex

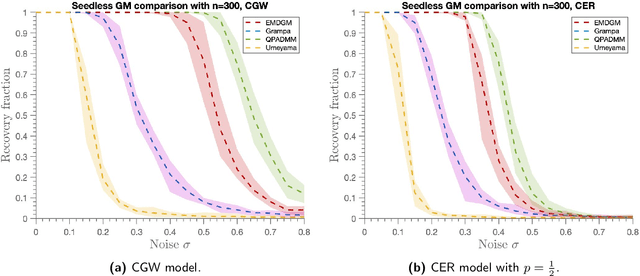
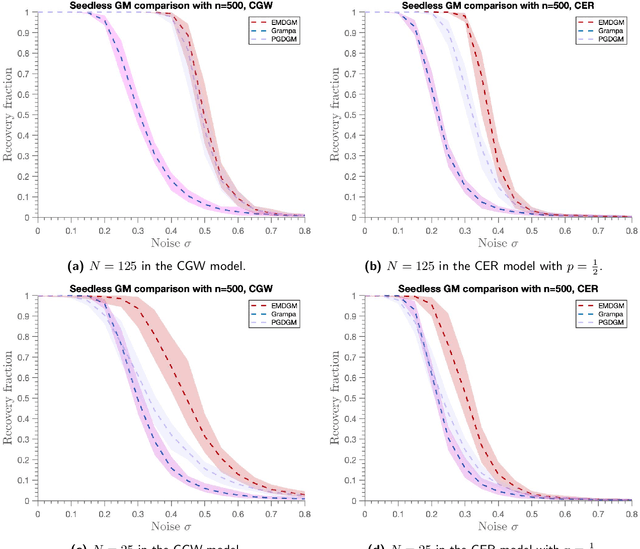
This paper addresses the Graph Matching problem, which consists of finding the best possible alignment between two input graphs, and has many applications in computer vision, network deanonymization and protein alignment. A common approach to tackle this problem is through convex relaxations of the NP-hard \emph{Quadratic Assignment Problem} (QAP). Here, we introduce a new convex relaxation onto the unit simplex and develop an efficient mirror descent scheme with closed-form iterations for solving this problem. Under the correlated Gaussian Wigner model, we show that the simplex relaxation admits a unique solution with high probability. In the noiseless case, this is shown to imply exact recovery of the ground truth permutation. Additionally, we establish a novel sufficiency condition for the input matrix in standard greedy rounding methods, which is less restrictive than the commonly used `diagonal dominance' condition. We use this condition to show exact one-step recovery of the ground truth (holding almost surely) via the mirror descent scheme, in the noiseless setting. We also use this condition to obtain significantly improved conditions for the GRAMPA algorithm [Fan et al. 2019] in the noiseless setting.

Learning linear dynamical systems under convex constraints

We consider the problem of identification of linear dynamical systems from a single trajectory. Recent results have predominantly focused on the setup where no structural assumption is made on the system matrix $A^* \in \mathbb{R}^{n \times n}$, and have consequently analyzed the ordinary least squares (OLS) estimator in detail. We assume prior structural information on $A^*$ is available, which can be captured in the form of a convex set $\mathcal{K}$ containing $A^*$. For the solution of the ensuing constrained least squares estimator, we derive non-asymptotic error bounds in the Frobenius norm which depend on the local size of the tangent cone of $\mathcal{K}$ at $A^*$. To illustrate the usefulness of this result, we instantiate it for the settings where, (i) $\mathcal{K}$ is a $d$ dimensional subspace of $\mathbb{R}^{n \times n}$, or (ii) $A^*$ is $k$-sparse and $\mathcal{K}$ is a suitably scaled $\ell_1$ ball. In the regimes where $d, k \ll n^2$, our bounds improve upon those obtained from the OLS estimator.

Dynamic Ranking and Translation Synchronization

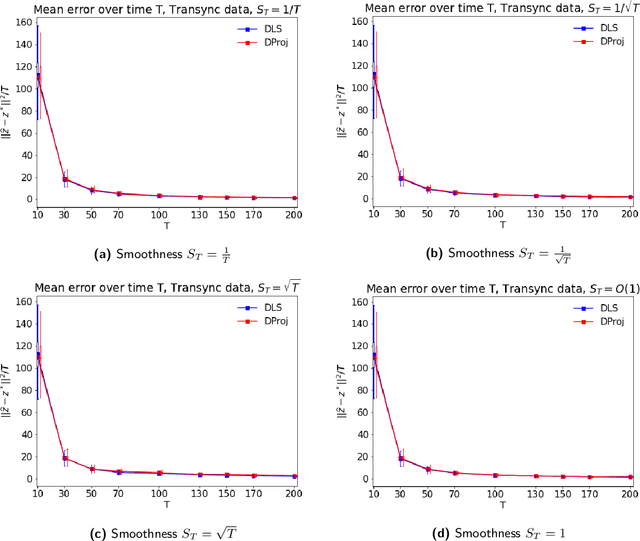
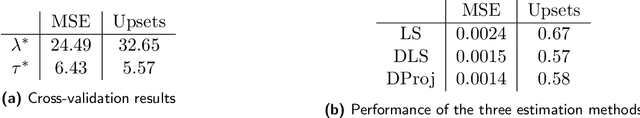
In many applications, such as sport tournaments or recommendation systems, we have at our disposal data consisting of pairwise comparisons between a set of $n$ items (or players). The objective is to use this data to infer the latent strength of each item and/or their ranking. Existing results for this problem predominantly focus on the setting consisting of a single comparison graph $G$. However, there exist scenarios (e.g., sports tournaments) where the the pairwise comparison data evolves with time. Theoretical results for this dynamic setting are relatively limited and is the focus of this paper. We study an extension of the \emph{translation synchronization} problem, to the dynamic setting. In this setup, we are given a sequence of comparison graphs $(G_t)_{t\in \mathcal{T}}$, where $\mathcal{T} \subset [0,1]$ is a grid representing the time domain, and for each item $i$ and time $t\in \mathcal{T}$ there is an associated unknown strength parameter $z^*_{t,i}\in \mathbb{R}$. We aim to recover, for $t\in\mathcal{T}$, the strength vector $z^*_t=(z^*_{t,1},\dots,z^*_{t,n})$ from noisy measurements of $z^*_{t,i}-z^*_{t,j}$, where $\{i,j\}$ is an edge in $G_t$. Assuming that $z^*_t$ evolves smoothly in $t$, we propose two estimators -- one based on a smoothness-penalized least squares approach and the other based on projection onto the low frequency eigenspace of a suitable smoothness operator. For both estimators, we provide finite sample bounds for the $\ell_2$ estimation error under the assumption that $G_t$ is connected for all $t\in \mathcal{T}$, thus proving the consistency of the proposed methods in terms of the grid size $|\mathcal{T}|$. We complement our theoretical findings with experiments on synthetic and real data.

Seeded graph matching for the correlated Wigner model via the projected power method

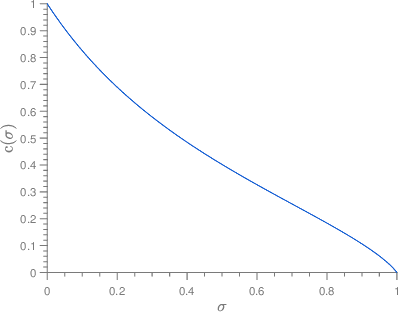
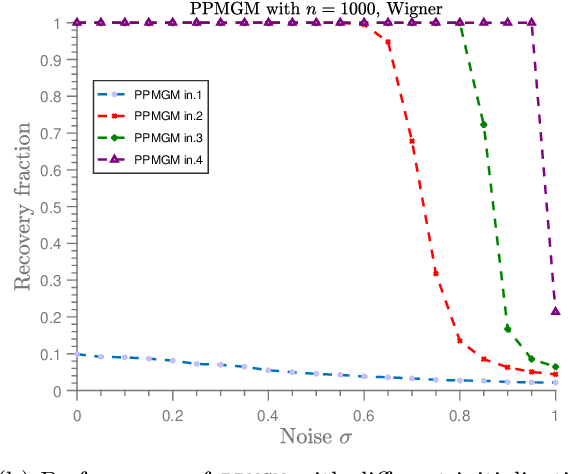
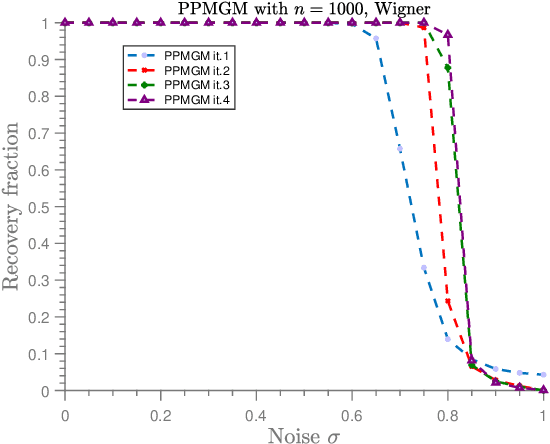
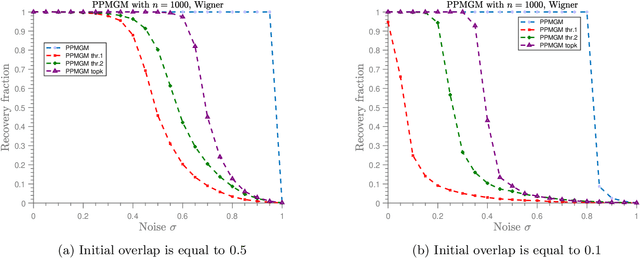
In the graph matching problem we observe two graphs $G,H$ and the goal is to find an assignment (or matching) between their vertices such that some measure of edge agreement is maximized. We assume in this work that the observed pair $G,H$ has been drawn from the correlated Wigner model -- a popular model for correlated weighted graphs -- where the entries of the adjacency matrices of $G$ and $H$ are independent Gaussians and each edge of $G$ is correlated with one edge of $H$ (determined by the unknown matching) with the edge correlation described by a parameter $\sigma\in [0,1)$. In this paper, we analyse the performance of the projected power method (PPM) as a seeded graph matching algorithm where we are given an initial partially correct matching (called the seed) as side information. We prove that if the seed is close enough to the ground-truth matching, then with high probability, PPM iteratively improves the seed and recovers the ground-truth matching (either partially or exactly) in $\mathcal{O}(\log n)$ iterations. Our results prove that PPM works even in regimes of constant $\sigma$, thus extending the analysis in (Mao et al.,2021) for the sparse Erd\"os-Renyi model to the (dense) Wigner model. As a byproduct of our analysis, we see that the PPM framework generalizes some of the state-of-art algorithms for seeded graph matching. We support and complement our theoretical findings with numerical experiments on synthetic data.

An iterative clustering algorithm for the Contextual Stochastic Block Model with optimality guarantees

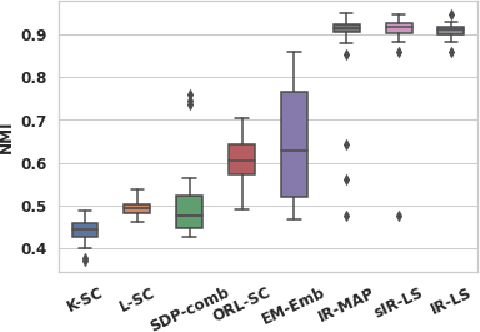
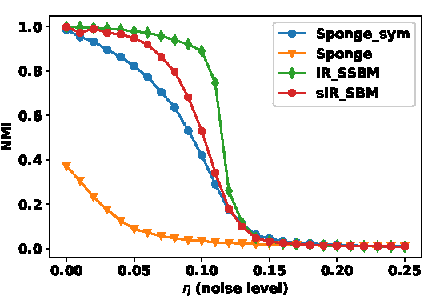
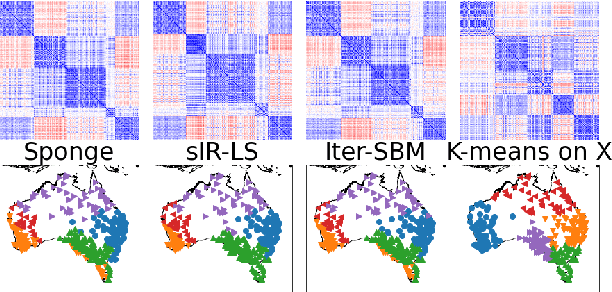
Real-world networks often come with side information that can help to improve the performance of network analysis tasks such as clustering. Despite a large number of empirical and theoretical studies conducted on network clustering methods during the past decade, the added value of side information and the methods used to incorporate it optimally in clustering algorithms are relatively less understood. We propose a new iterative algorithm to cluster networks with side information for nodes (in the form of covariates) and show that our algorithm is optimal under the Contextual Symmetric Stochastic Block Model. Our algorithm can be applied to general Contextual Stochastic Block Models and avoids hyperparameter tuning in contrast to previously proposed methods. We confirm our theoretical results on synthetic data experiments where our algorithm significantly outperforms other methods, and show that it can also be applied to signed graphs. Finally we demonstrate the practical interest of our method on real data.

Recovering Hölder smooth functions from noisy modulo samples

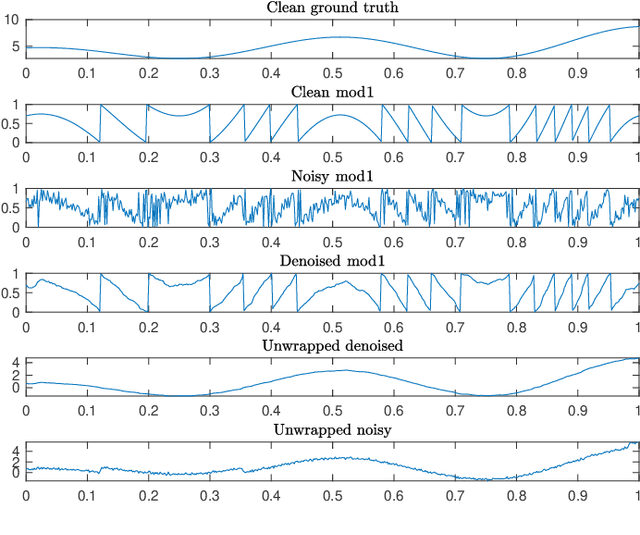
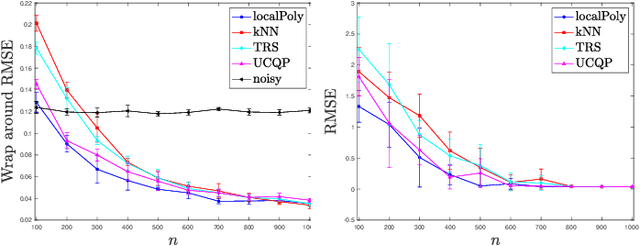
In signal processing, several applications involve the recovery of a function given noisy modulo samples. The setting considered in this paper is that the samples corrupted by an additive Gaussian noise are wrapped due to the modulo operation. Typical examples of this problem arise in phase unwrapping problems or in the context of self-reset analog to digital converters. We consider a fixed design setting where the modulo samples are given on a regular grid. Then, a three stage recovery strategy is proposed to recover the ground truth signal up to a global integer shift. The first stage denoises the modulo samples by using local polynomial estimators. In the second stage, an unwrapping algorithm is applied to the denoised modulo samples on the grid. Finally, a spline based quasi-interpolant operator is used to yield an estimate of the ground truth function up to a global integer shift. For a function in H\"older class, uniform error rates are given for recovery performance with high probability. This extends recent results obtained by Fanuel and Tyagi for Lipschitz smooth functions wherein $k$NN regression was used in the denoising step.

Dynamic Ranking with the BTL Model: A Nearest Neighbor based Rank Centrality Method

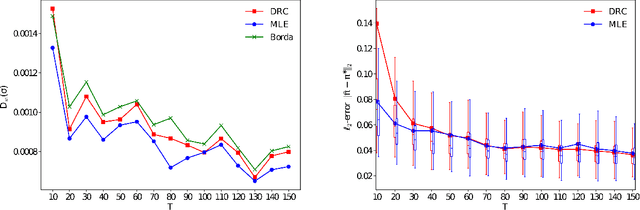
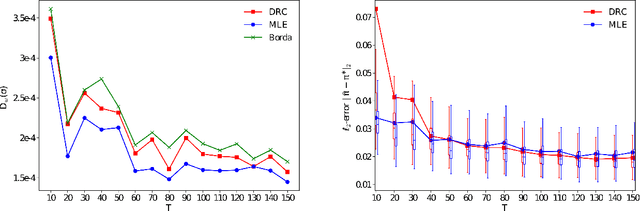
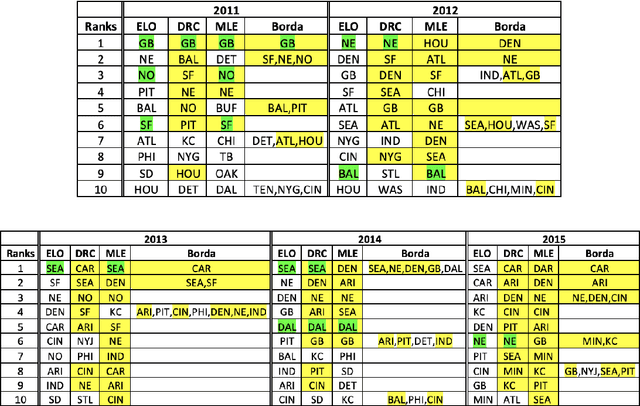
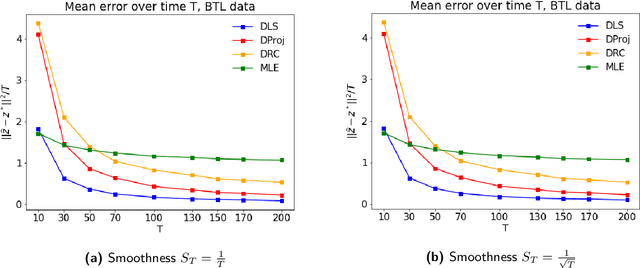
Many applications such as recommendation systems or sports tournaments involve pairwise comparisons within a collection of $n$ items, the goal being to aggregate the binary outcomes of the comparisons in order to recover the latent strength and/or global ranking of the items. In recent years, this problem has received significant interest from a theoretical perspective with a number of methods being proposed, along with associated statistical guarantees under the assumption of a suitable generative model. While these results typically collect the pairwise comparisons as one comparison graph $G$, however in many applications - such as the outcomes of soccer matches during a tournament - the nature of pairwise outcomes can evolve with time. Theoretical results for such a dynamic setting are relatively limited compared to the aforementioned static setting. We study in this paper an extension of the classic BTL (Bradley-Terry-Luce) model for the static setting to our dynamic setup under the assumption that the probabilities of the pairwise outcomes evolve smoothly over the time domain $[0,1]$. Given a sequence of comparison graphs $(G_{t'})_{t' \in \mathcal{T}}$ on a regular grid $\mathcal{T} \subset [0,1]$, we aim at recovering the latent strengths of the items $w_t \in \mathbb{R}^n$ at any time $t \in [0,1]$. To this end, we adapt the Rank Centrality method - a popular spectral approach for ranking in the static case - by locally averaging the available data on a suitable neighborhood of $t$. When $(G_{t'})_{t' \in \mathcal{T}}$ is a sequence of Erd\"os-Renyi graphs, we provide non-asymptotic $\ell_2$ and $\ell_{\infty}$ error bounds for estimating $w_t^*$ which in particular establishes the consistency of this method in terms of $n$, and the grid size $\lvert\mathcal{T}\rvert$. We also complement our theoretical analysis with experiments on real and synthetic data.

Clustering multilayer graphs with missing nodes

Relationship between agents can be conveniently represented by graphs. When these relationships have different modalities, they are better modelled by multilayer graphs where each layer is associated with one modality. Such graphs arise naturally in many contexts including biological and social networks. Clustering is a fundamental problem in network analysis where the goal is to regroup nodes with similar connectivity profiles. In the past decade, various clustering methods have been extended from the unilayer setting to multilayer graphs in order to incorporate the information provided by each layer. While most existing works assume - rather restrictively - that all layers share the same set of nodes, we propose a new framework that allows for layers to be defined on different sets of nodes. In particular, the nodes not recorded in a layer are treated as missing. Within this paradigm, we investigate several generalizations of well-known clustering methods in the complete setting to the incomplete one and prove some consistency results under the Multi-Layer Stochastic Block Model assumption. Our theoretical results are complemented by thorough numerical comparisons between our proposed algorithms on synthetic data, and also on real datasets, thus highlighting the promising behaviour of our methods in various settings.