Synchronization on circles and spheres with nonlinear interactions

We consider the dynamics of $n$ points on a sphere in $\mathbb{R}^d$ ($d \geq 2$) which attract each other according to a function $\varphi$ of their inner products. When $\varphi$ is linear ($\varphi(t) = t$), the points converge to a common value (i.e., synchronize) in various connectivity scenarios: this is part of classical work on Kuramoto oscillator networks. When $\varphi$ is exponential ($\varphi(t) = e^{\beta t}$), these dynamics correspond to a limit of how idealized transformers process data, as described by Geshkovski et al. (2024). Accordingly, they ask whether synchronization occurs for exponential $\varphi$. In the context of consensus for multi-agent control, Markdahl et al. (2018) show that for $d \geq 3$ (spheres), if the interaction graph is connected and $\varphi$ is increasing and convex, then the system synchronizes. What is the situation on circles ($d=2$)? First, we show that $\varphi$ being increasing and convex is no longer sufficient. Then we identify a new condition (that the Taylor coefficients of $\varphi'$ are decreasing) under which we do have synchronization on the circle. In so doing, we provide some answers to the open problems posed by Geshkovski et al. (2024).

Online false discovery rate control for anomaly detection in time series

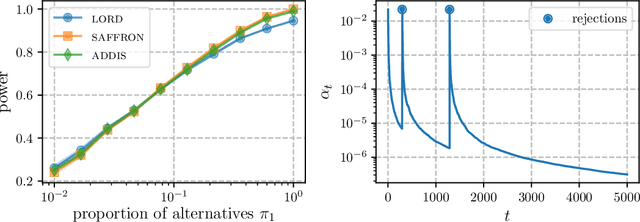
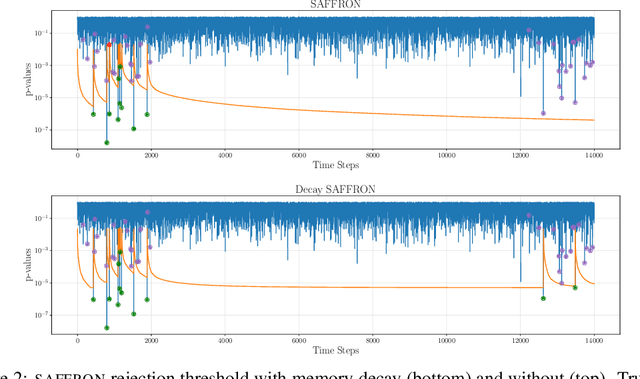
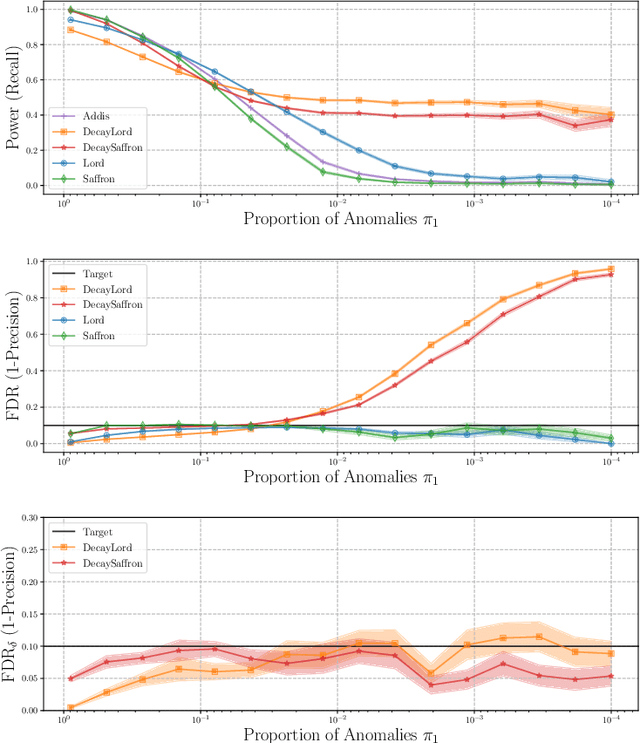
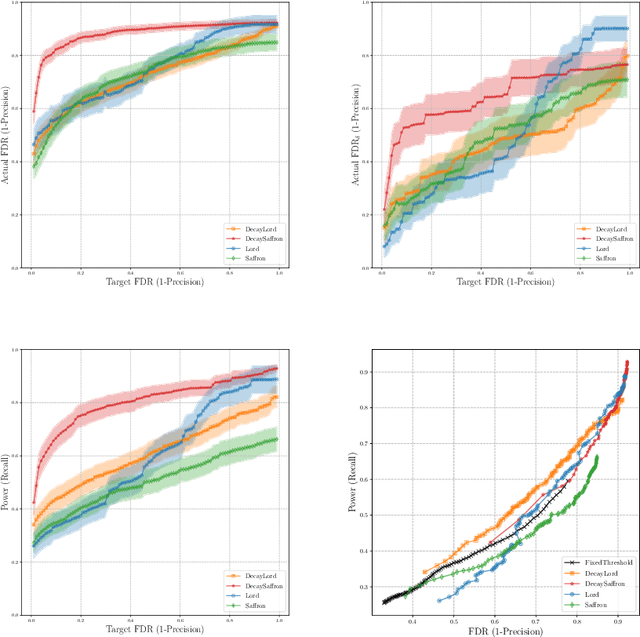
This article proposes novel rules for false discovery rate control (FDRC) geared towards online anomaly detection in time series. Online FDRC rules allow to control the properties of a sequence of statistical tests. In the context of anomaly detection, the null hypothesis is that an observation is normal and the alternative is that it is anomalous. FDRC rules allow users to target a lower bound on precision in unsupervised settings. The methods proposed in this article overcome short-comings of previous FDRC rules in the context of anomaly detection, in particular ensuring that power remains high even when the alternative is exceedingly rare (typical in anomaly detection) and the test statistics are serially dependent (typical in time series). We show the soundness of these rules in both theory and experiments.

A simple and effective predictive resource scaling heuristic for large-scale cloud applications

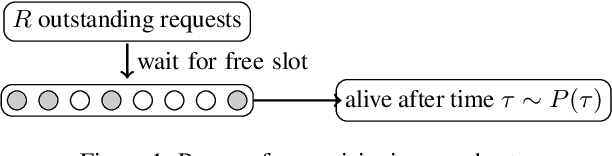
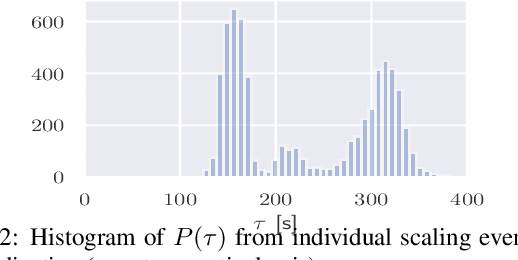
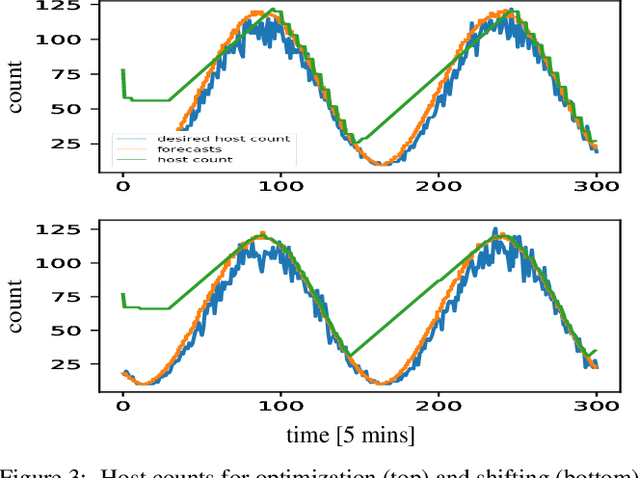
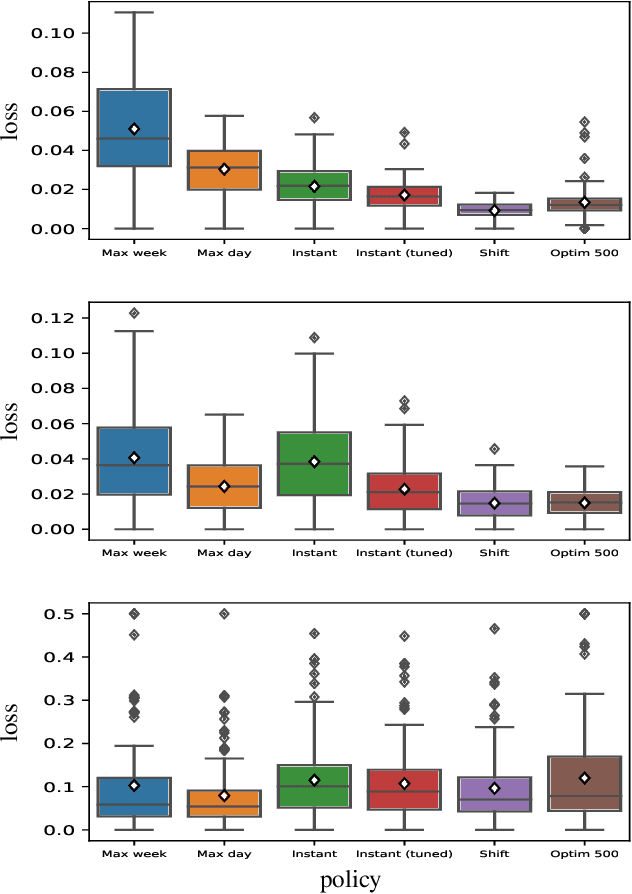
We propose a simple yet effective policy for the predictive auto-scaling of horizontally scalable applications running in cloud environments, where compute resources can only be added with a delay, and where the deployment throughput is limited. Our policy uses a probabilistic forecast of the workload to make scaling decisions dependent on the risk aversion of the application owner. We show in our experiments using real-world and synthetic data that this policy compares favorably to mathematically more sophisticated approaches as well as to simple benchmark policies.

FANOK: Knockoffs in Linear Time

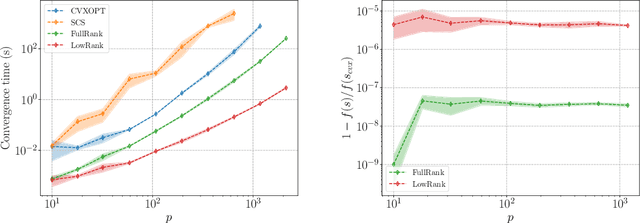
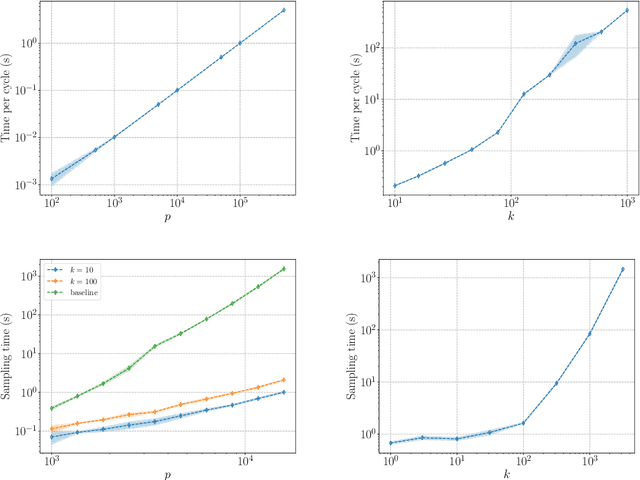
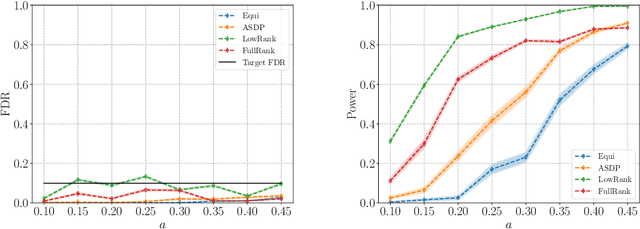
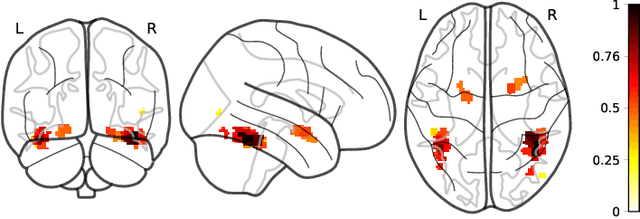
We describe a series of algorithms that efficiently implement Gaussian model-X knockoffs to control the false discovery rate on large scale feature selection problems. Identifying the knockoff distribution requires solving a large scale semidefinite program for which we derive several efficient methods. One handles generic covariance matrices, has a complexity scaling as $O(p^3)$ where $p$ is the ambient dimension, while another assumes a rank $k$ factor model on the covariance matrix to reduce this complexity bound to $O(pk^2)$. We also derive efficient procedures to both estimate factor models and sample knockoff covariates with complexity linear in the dimension. We test our methods on problems with $p$ as large as $500,000$.

Error Feedback Fixes SignSGD and other Gradient Compression Schemes

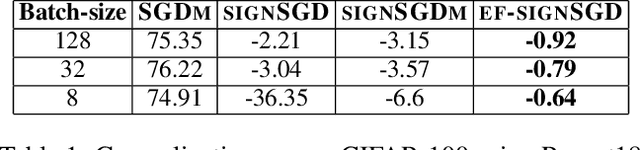
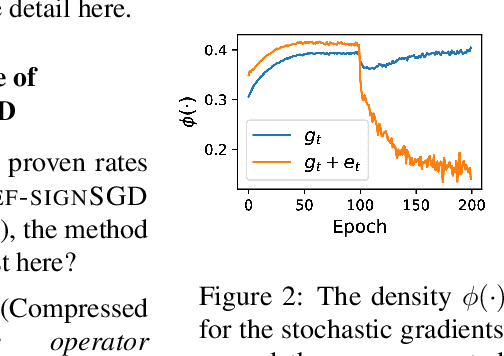
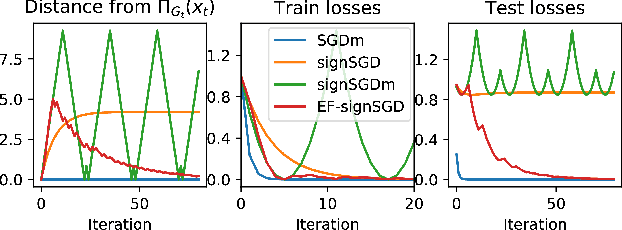
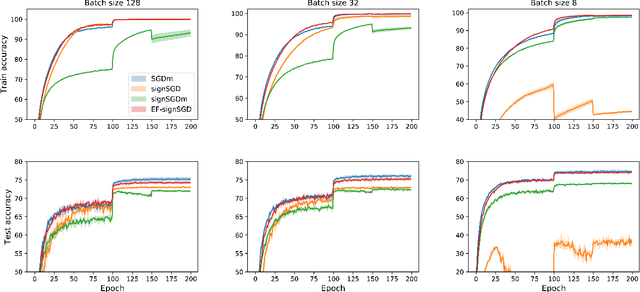
Sign-based algorithms (e.g. signSGD) have been proposed as a biased gradient compression technique to alleviate the communication bottleneck in training large neural networks across multiple workers. We show simple convex counter-examples where signSGD does not converge to the optimum. Further, even when it does converge, signSGD may generalize poorly when compared with SGD. These issues arise because of the biased nature of the sign compression operator. We then show that using error-feedback, i.e. incorporating the error made by the compression operator into the next step, overcomes these issues. We prove that our algorithm EF-SGD achieves the same rate of convergence as SGD without any additional assumptions for arbitrary compression operators (including the sign operator), indicating that we get gradient compression for free. Our experiments thoroughly substantiate the theory showing the superiority of our algorithm.