Distillation Robustifies Unlearning

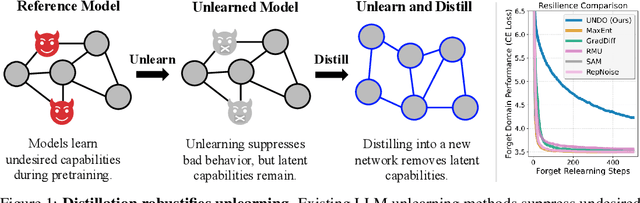
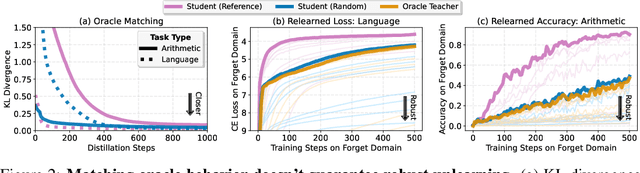
Current LLM unlearning methods are not robust: they can be reverted easily with a few steps of finetuning. This is true even for the idealized unlearning method of training to imitate an oracle model that was never exposed to unwanted information, suggesting that output-based finetuning is insufficient to achieve robust unlearning. In a similar vein, we find that training a randomly initialized student to imitate an unlearned model transfers desired behaviors while leaving undesired capabilities behind. In other words, distillation robustifies unlearning. Building on this insight, we propose Unlearn-Noise-Distill-on-Outputs (UNDO), a scalable method that distills an unlearned model into a partially noised copy of itself. UNDO introduces a tunable tradeoff between compute cost and robustness, establishing a new Pareto frontier on synthetic language and arithmetic tasks. At its strongest setting, UNDO matches the robustness of a model retrained from scratch with perfect data filtering while using only 60-80% of the compute and requiring only 0.01% of the pretraining data to be labeled. We also show that UNDO robustifies unlearning on the more realistic Weapons of Mass Destruction Proxy (WMDP) benchmark. Since distillation is widely used in practice, incorporating an unlearning step beforehand offers a convenient path to robust capability removal.

The Persian Rug: solving toy models of superposition using large-scale symmetries

We present a complete mechanistic description of the algorithm learned by a minimal non-linear sparse data autoencoder in the limit of large input dimension. The model, originally presented in arXiv:2209.10652, compresses sparse data vectors through a linear layer and decompresses using another linear layer followed by a ReLU activation. We notice that when the data is permutation symmetric (no input feature is privileged) large models reliably learn an algorithm that is sensitive to individual weights only through their large-scale statistics. For these models, the loss function becomes analytically tractable. Using this understanding, we give the explicit scalings of the loss at high sparsity, and show that the model is near-optimal among recently proposed architectures. In particular, changing or adding to the activation function any elementwise or filtering operation can at best improve the model's performance by a constant factor. Finally, we forward-engineer a model with the requisite symmetries and show that its loss precisely matches that of the trained models. Unlike the trained model weights, the low randomness in the artificial weights results in miraculous fractal structures resembling a Persian rug, to which the algorithm is oblivious. Our work contributes to neural network interpretability by introducing techniques for understanding the structure of autoencoders. Code to reproduce our results can be found at https://github.com/KfirD/PersianRug .