Consistent Discretization and Minimization of the L1 Norm on Manifolds

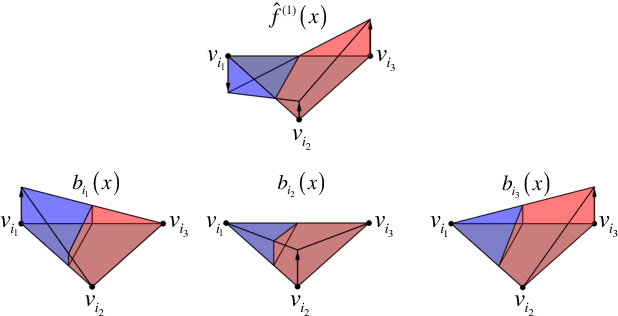
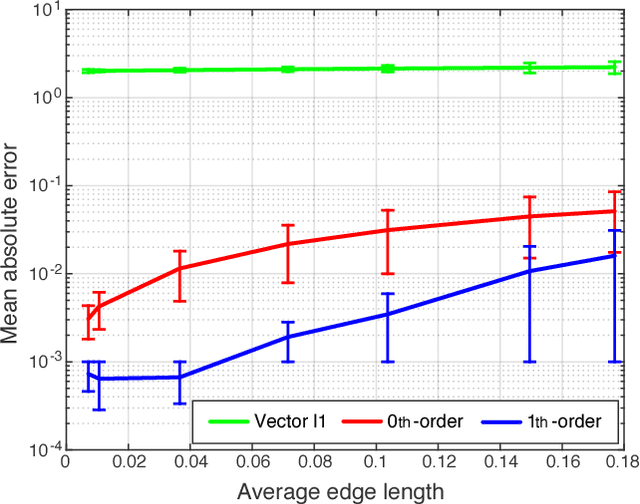
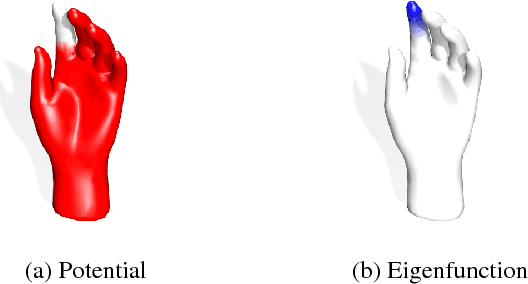
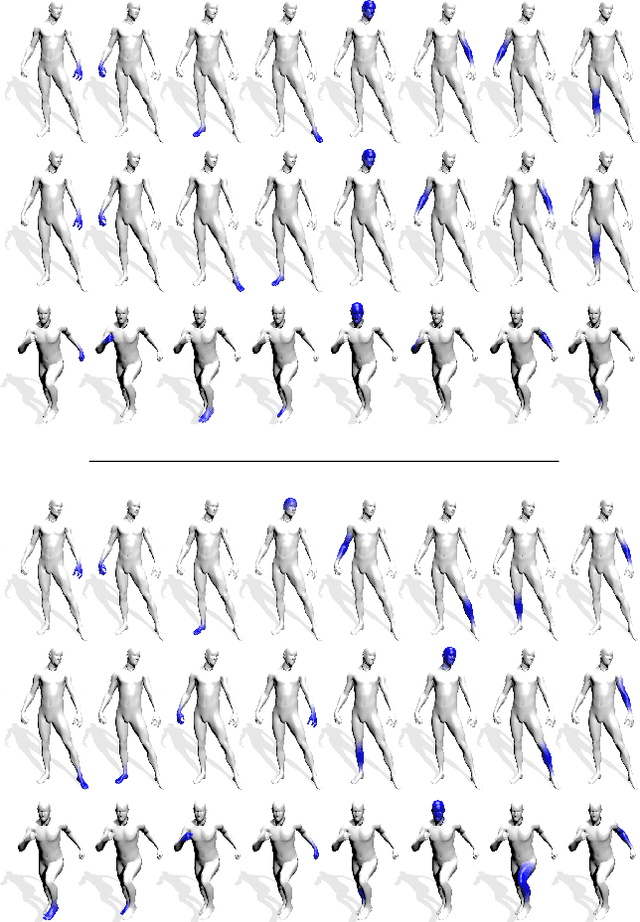
The L1 norm has been tremendously popular in signal and image processing in the past two decades due to its sparsity-promoting properties. More recently, its generalization to non-Euclidean domains has been found useful in shape analysis applications. For example, in conjunction with the minimization of the Dirichlet energy, it was shown to produce a compactly supported quasi-harmonic orthonormal basis, dubbed as compressed manifold modes. The continuous L1 norm on the manifold is often replaced by the vector l1 norm applied to sampled functions. We show that such an approach is incorrect in the sense that it does not consistently discretize the continuous norm and warn against its sensitivity to the specific sampling. We propose two alternative discretizations resulting in an iteratively-reweighed l2 norm. We demonstrate the proposed strategy on the compressed modes problem, which reduces to a sequence of simple eigendecomposition problems not requiring non-convex optimization on Stiefel manifolds and producing more stable and accurate results.

FPGA system for real-time computational extended depth of field imaging using phase aperture coding

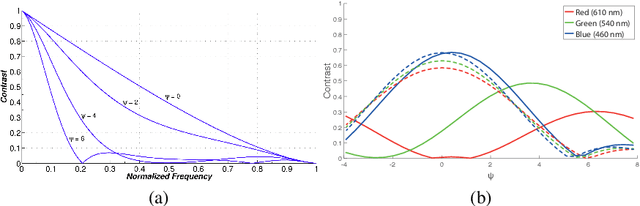
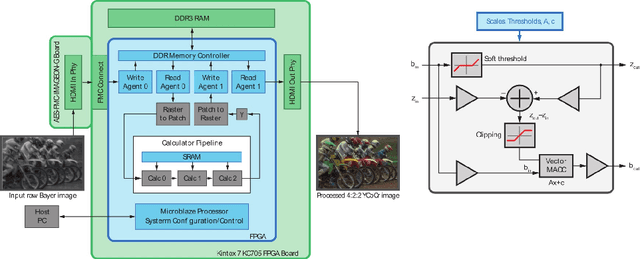
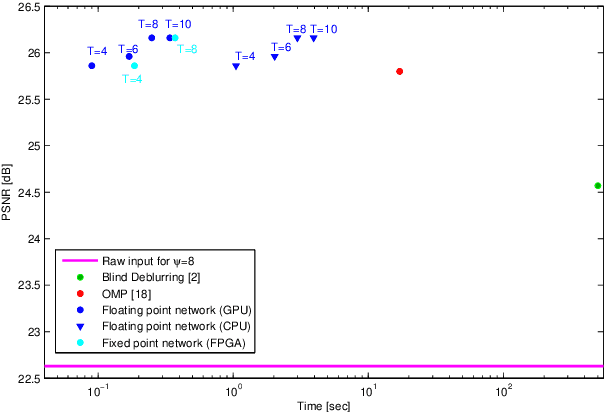
We present a proof-of-concept end-to-end system for computational extended depth of field (EDOF) imaging. The acquisition is performed through a phase-coded aperture implemented by placing a thin wavelength-dependent optical mask inside the pupil of a conventional camera lens, as a result of which, each color channel is focused at a different depth. The reconstruction process receives the raw Bayer image as the input, and performs blind estimation of the output color image in focus at an extended range of depths using a patch-wise sparse prior. We present a fast non-iterative reconstruction algorithm operating with constant latency in fixed-point arithmetics and achieving real-time performance in a prototype FPGA implementation. The output of the system, on simulated and real-life scenes, is qualitatively and quantitatively better than the result of clear-aperture imaging followed by state-of-the-art blind deblurring.

Bayesian Inference of Bijective Non-Rigid Shape Correspondence

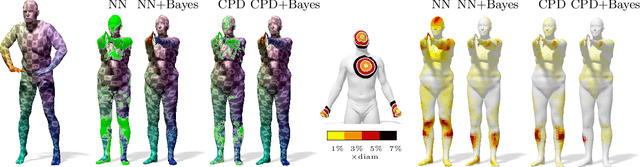
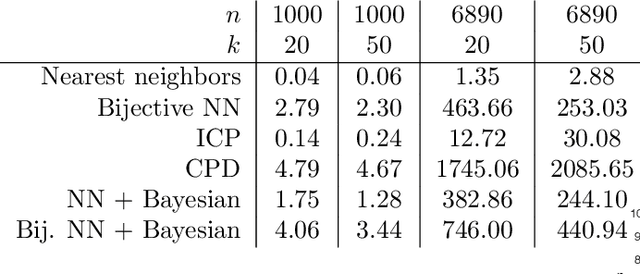
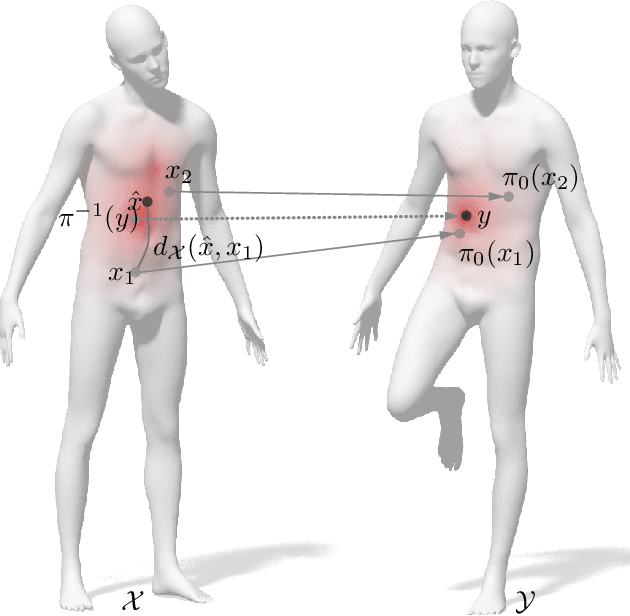
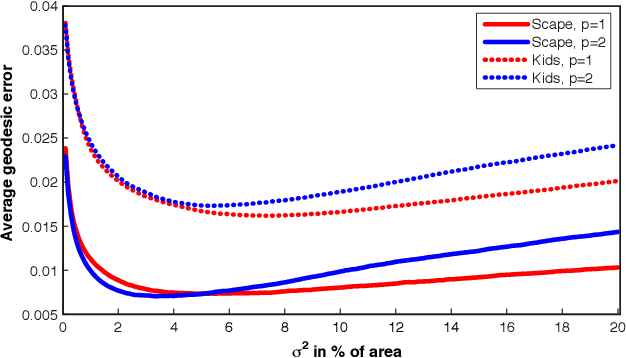
Many algorithms for the computation of correspondences between deformable shapes rely on some variant of nearest neighbor matching in a descriptor space. Such are, for example, various point-wise correspondence recovery algorithms used as a postprocessing stage in the functional correspondence framework. In this paper, we show that such frequently used techniques in practice suffer from lack of accuracy and result in poor surjectivity. We propose an alternative recovery technique guaranteeing a bijective correspondence and producing significantly higher accuracy. We derive the proposed method from a statistical framework of Bayesian inference and demonstrate its performance on several challenging deformable 3D shape matching datasets.

Image reconstruction from dense binary pixels

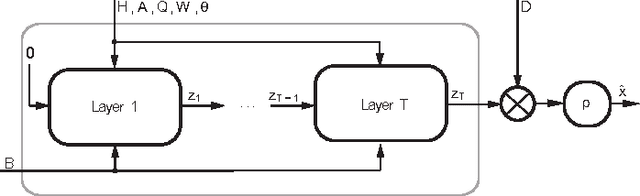
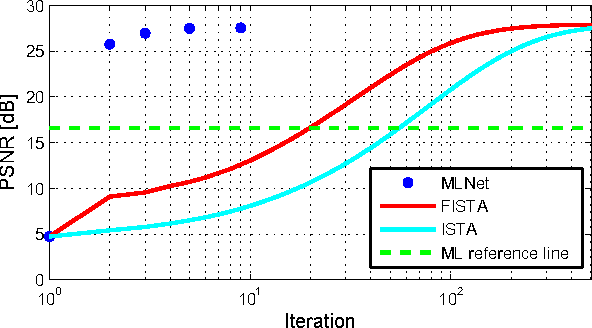
Recently, the dense binary pixel Gigavision camera had been introduced, emulating a digital version of the photographic film. While seems to be a promising solution for HDR imaging, its output is not directly usable and requires an image reconstruction process. In this work, we formulate this problem as the minimization of a convex objective combining a maximum-likelihood term with a sparse synthesis prior. We present MLNet - a novel feed-forward neural network, producing acceptable output quality at a fixed complexity and is two orders of magnitude faster than iterative algorithms. We present state of the art results in the abstract.

A Picture is Worth a Billion Bits: Real-Time Image Reconstruction from Dense Binary Pixels

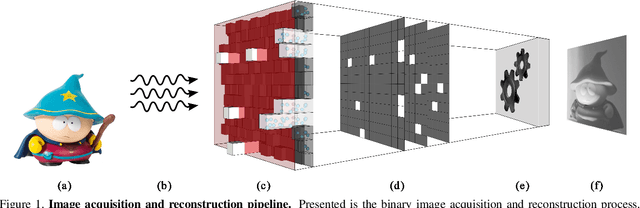
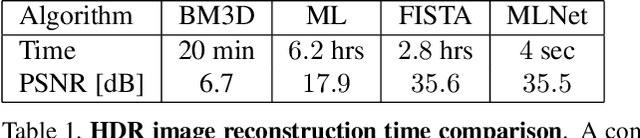
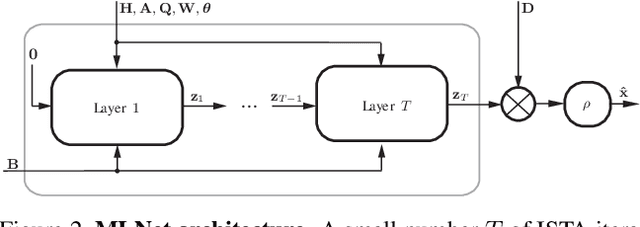
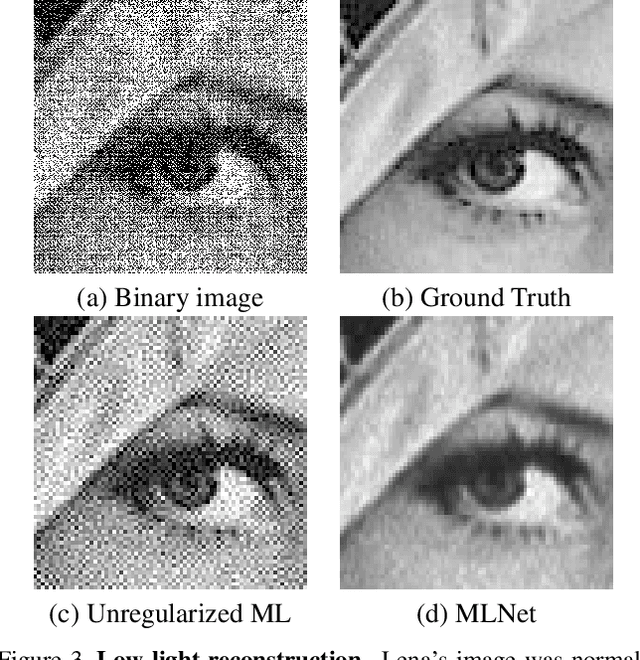
The pursuit of smaller pixel sizes at ever increasing resolution in digital image sensors is mainly driven by the stringent price and form-factor requirements of sensors and optics in the cellular phone market. Recently, Eric Fossum proposed a novel concept of an image sensor with dense sub-diffraction limit one-bit pixels jots, which can be considered a digital emulation of silver halide photographic film. This idea has been recently embodied as the EPFL Gigavision camera. A major bottleneck in the design of such sensors is the image reconstruction process, producing a continuous high dynamic range image from oversampled binary measurements. The extreme quantization of the Poisson statistics is incompatible with the assumptions of most standard image processing and enhancement frameworks. The recently proposed maximum-likelihood (ML) approach addresses this difficulty, but suffers from image artifacts and has impractically high computational complexity. In this work, we study a variant of a sensor with binary threshold pixels and propose a reconstruction algorithm combining an ML data fitting term with a sparse synthesis prior. We also show an efficient hardware-friendly real-time approximation of this inverse operator.Promising results are shown on synthetic data as well as on HDR data emulated using multiple exposures of a regular CMOS sensor.

ASIST: Automatic Semantically Invariant Scene Transformation

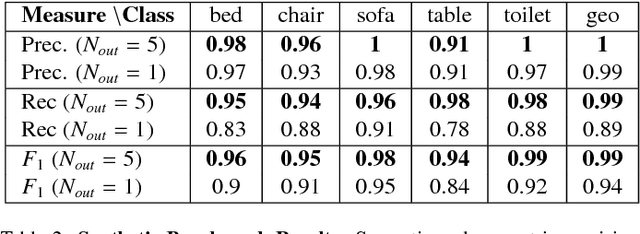
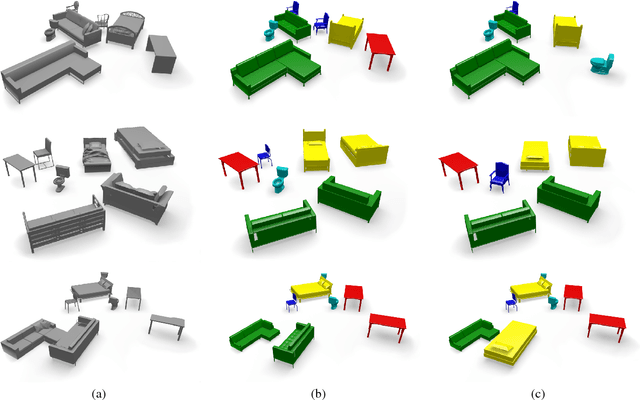
We present ASIST, a technique for transforming point clouds by replacing objects with their semantically equivalent counterparts. Transformations of this kind have applications in virtual reality, repair of fused scans, and robotics. ASIST is based on a unified formulation of semantic labeling and object replacement; both result from minimizing a single objective. We present numerical tools for the efficient solution of this optimization problem. The method is experimentally assessed on new datasets of both synthetic and real point clouds, and is additionally compared to two recent works on object replacement on data from the corresponding papers.

Random Forests Can Hash

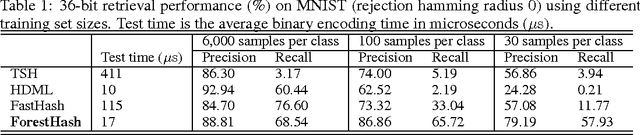
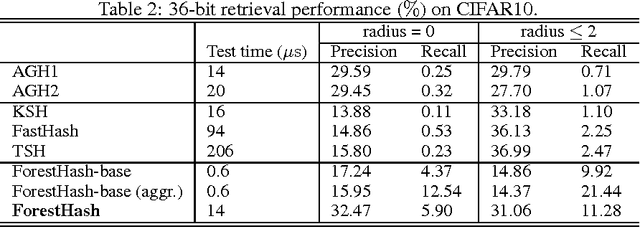
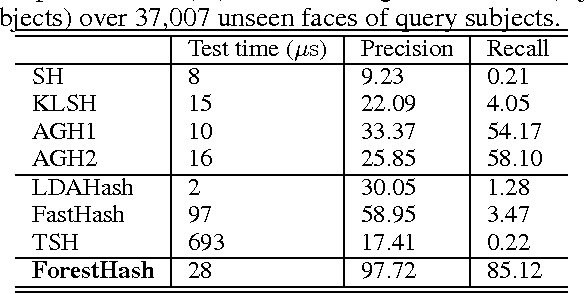
Hash codes are a very efficient data representation needed to be able to cope with the ever growing amounts of data. We introduce a random forest semantic hashing scheme with information-theoretic code aggregation, showing for the first time how random forest, a technique that together with deep learning have shown spectacular results in classification, can also be extended to large-scale retrieval. Traditional random forest fails to enforce the consistency of hashes generated from each tree for the same class data, i.e., to preserve the underlying similarity, and it also lacks a principled way for code aggregation across trees. We start with a simple hashing scheme, where independently trained random trees in a forest are acting as hashing functions. We the propose a subspace model as the splitting function, and show that it enforces the hash consistency in a tree for data from the same class. We also introduce an information-theoretic approach for aggregating codes of individual trees into a single hash code, producing a near-optimal unique hash for each class. Experiments on large-scale public datasets are presented, showing that the proposed approach significantly outperforms state-of-the-art hashing methods for retrieval tasks.

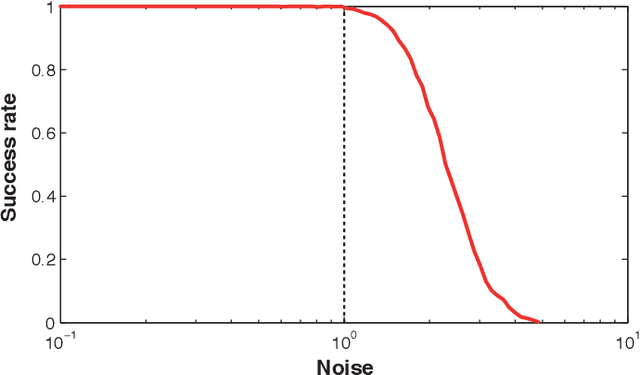
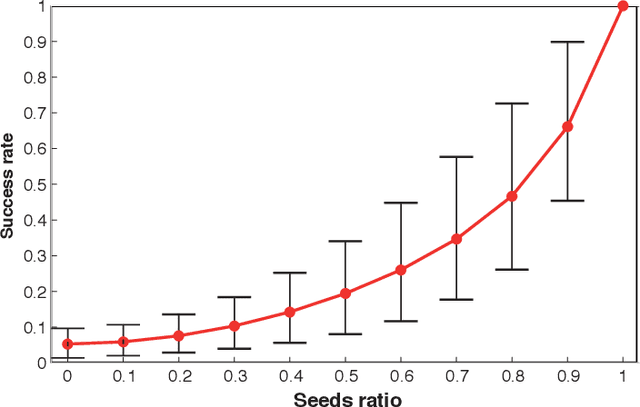
Graph matching: relax or not?

We consider the problem of exact and inexact matching of weighted undirected graphs, in which a bijective correspondence is sought to minimize a quadratic weight disagreement. This computationally challenging problem is often relaxed as a convex quadratic program, in which the space of permutations is replaced by the space of doubly-stochastic matrices. However, the applicability of such a relaxation is poorly understood. We define a broad class of friendly graphs characterized by an easily verifiable spectral property. We prove that for friendly graphs, the convex relaxation is guaranteed to find the exact isomorphism or certify its inexistence. This result is further extended to approximately isomorphic graphs, for which we develop an explicit bound on the amount of weight disagreement under which the relaxation is guaranteed to find the globally optimal approximate isomorphism. We also show that in many cases, the graph matching problem can be further harmlessly relaxed to a convex quadratic program with only n separable linear equality constraints, which is substantially more efficient than the standard relaxation involving 2n equality and n^2 inequality constraints. Finally, we show that our results are still valid for unfriendly graphs if additional information in the form of seeds or attributes is allowed, with the latter satisfying an easy to verify spectral characteristic.

Learning Efficient Structured Sparse Models

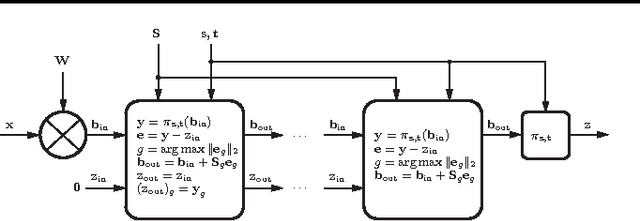
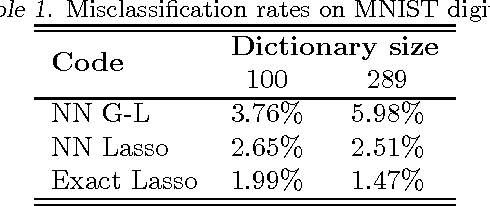
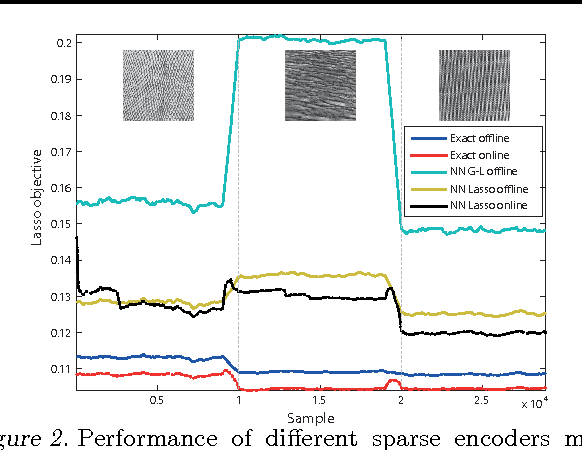
We present a comprehensive framework for structured sparse coding and modeling extending the recent ideas of using learnable fast regressors to approximate exact sparse codes. For this purpose, we develop a novel block-coordinate proximal splitting method for the iterative solution of hierarchical sparse coding problems, and show an efficient feed forward architecture derived from its iteration. This architecture faithfully approximates the exact structured sparse codes with a fraction of the complexity of the standard optimization methods. We also show that by using different training objective functions, learnable sparse encoders are no longer restricted to be mere approximants of the exact sparse code for a pre-given dictionary, as in earlier formulations, but can be rather used as full-featured sparse encoders or even modelers. A simple implementation shows several orders of magnitude speedup compared to the state-of-the-art at minimal performance degradation, making the proposed framework suitable for real time and large-scale applications.