Guided Incremental Local Densification for Accelerated Sampling-based Motion Planning

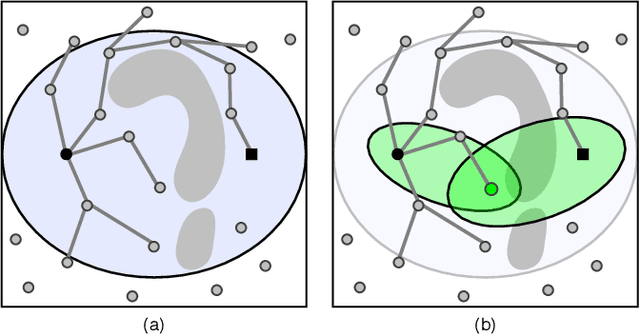
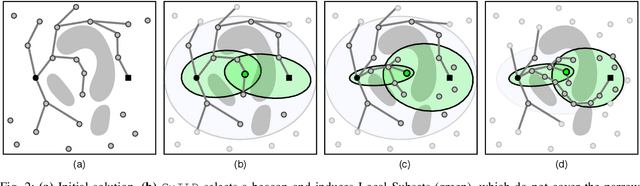
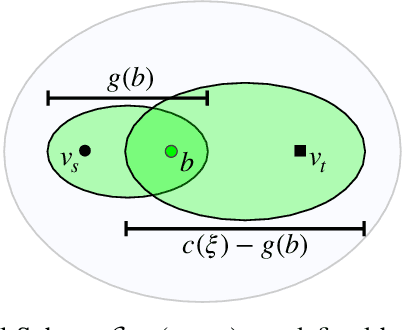
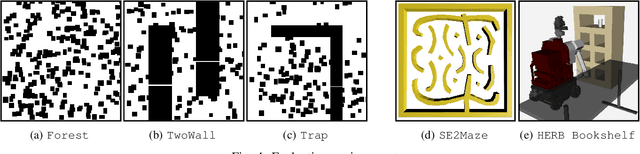
Sampling-based motion planners rely on incremental densification to discover progressively shorter paths. After computing feasible path $\xi$ between start $x_s$ and goal $x_t$, the Informed Set (IS) prunes the configuration space $\mathcal{C}$ by conservatively eliminating points that cannot yield shorter paths. Densification via sampling from this Informed Set retains asymptotic optimality of sampling from the entire configuration space. For path length $c(\xi)$ and Euclidean heuristic $h$, $IS = \{ x | x \in \mathcal{C}, h(x_s, x) + h(x, x_t) \leq c(\xi) \}$. Relying on the heuristic can render the IS especially conservative in high dimensions or complex environments. Furthermore, the IS only shrinks when shorter paths are discovered. Thus, the computational effort from each iteration of densification and planning is wasted if it fails to yield a shorter path, despite improving the cost-to-come for vertices in the search tree. Our key insight is that even in such a failure, shorter paths to vertices in the search tree (rather than just the goal) can immediately improve the planner's sampling strategy. Guided Incremental Local Densification (GuILD) leverages this information to sample from Local Subsets of the IS. We show that GuILD significantly outperforms uniform sampling of the Informed Set in simulated $\mathbb{R}^2$, $SE(2)$ environments and manipulation tasks in $\mathbb{R}^7$.

Posterior Sampling for Anytime Motion Planning on Graphs with Expensive-to-Evaluate Edges

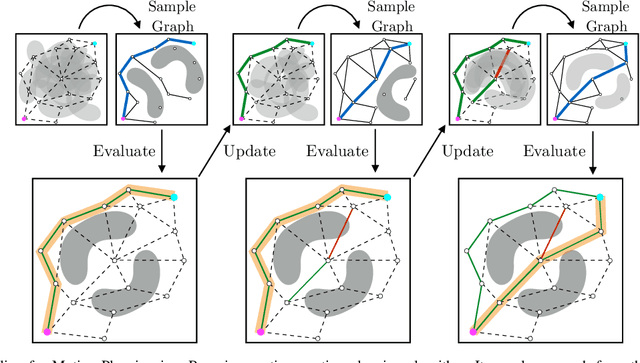
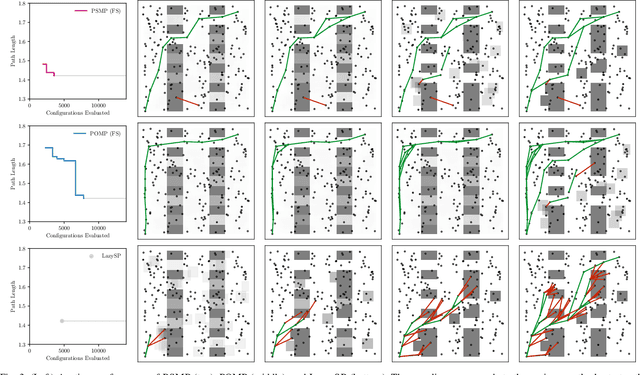
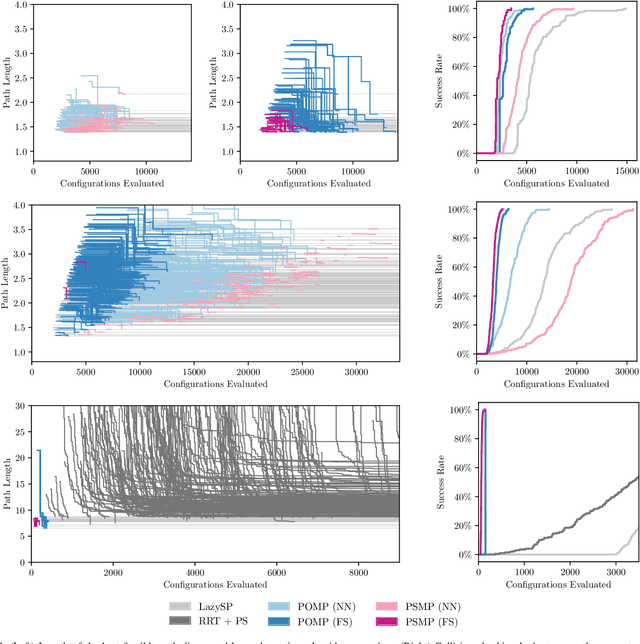
Collision checking is a computational bottleneck in motion planning, requiring lazy algorithms that explicitly reason about when to perform this computation. Optimism in the face of collision uncertainty minimizes the number of checks before finding the shortest path. However, this may take a prohibitively long time to compute, with no other feasible paths discovered during this period. For many real-time applications, we instead demand strong anytime performance, defined as minimizing the cumulative lengths of the feasible paths yielded over time. We introduce Posterior Sampling for Motion Planning (PSMP), an anytime lazy motion planning algorithm that leverages learned posteriors on edge collisions to quickly discover an initial feasible path and progressively yield shorter paths. PSMP obtains an expected regret bound of $\tilde{O}(\sqrt{\mathcal{S} \mathcal{A} T})$ and outperforms comparative baselines on a set of 2D and 7D planning problems.

LEGO: Leveraging Experience in Roadmap Generation for Sampling-Based Planning

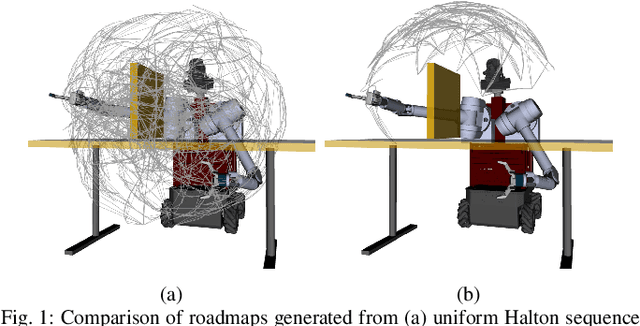
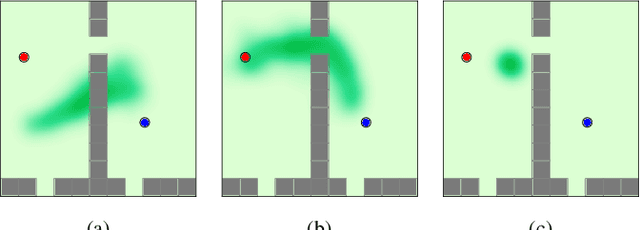
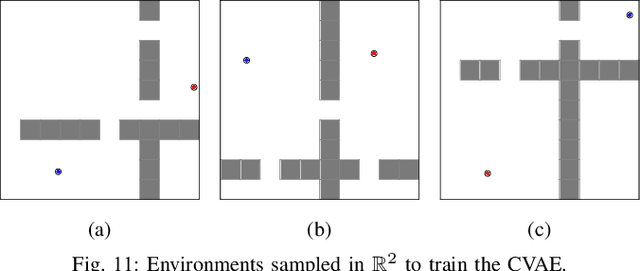
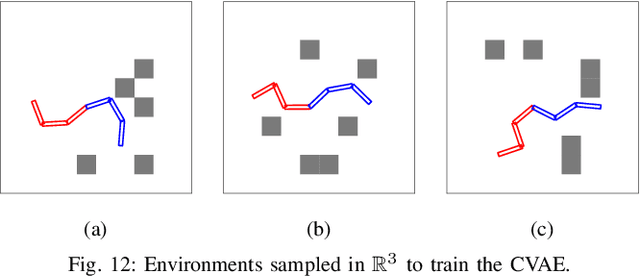
We consider the problem of leveraging prior experience to generate roadmaps in sampling-based motion planning. A desirable roadmap is one that is sparse, allowing for fast search, with nodes spread out at key locations such that a low-cost feasible path exists. An increasingly popular approach is to learn a distribution of nodes that would produce such a roadmap. State-of-the-art is to train a conditional variational auto-encoder (CVAE) on the prior dataset with the shortest paths as target input. While this is quite effective on many problems, we show it can fail in the face of complex obstacle configurations or mismatch between training and testing. We present an algorithm LEGO that addresses these issues by training the CVAE with target samples that satisfy two important criteria. Firstly, these samples belong only to bottleneck regions along near-optimal paths that are otherwise difficult-to-sample with a uniform sampler. Secondly, these samples are spread out across diverse regions to maximize the likelihood of a feasible path existing. We formally define these properties and prove performance guarantees for LEGO. We extensively evaluate LEGO on a range of planning problems, including robot arm planning, and report significant gains over heuristics as well as learned baselines.

Generalized Lazy Search for Robot Motion Planning: Interleaving Search and Edge Evaluation via Event-based Toggles

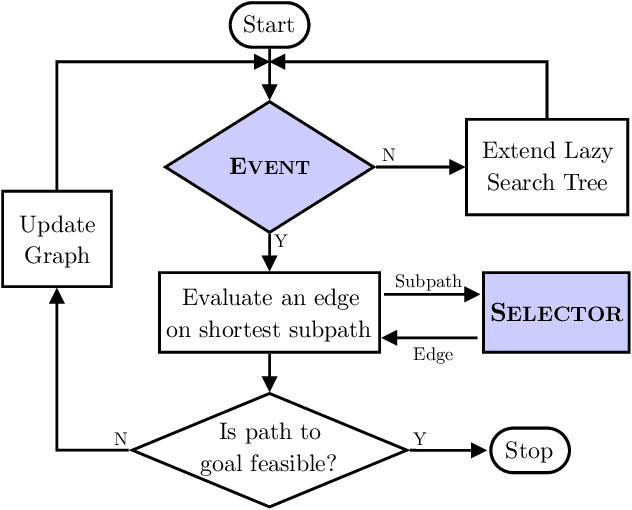
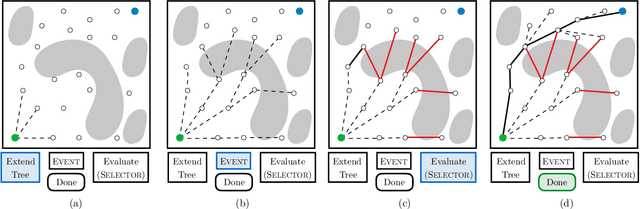
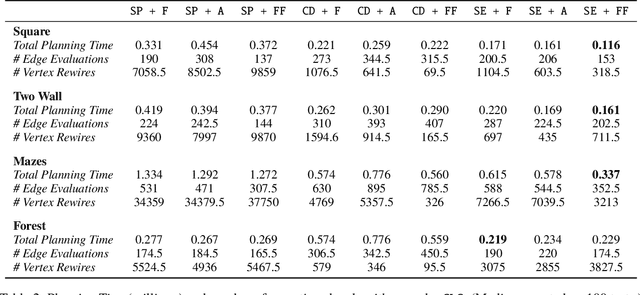
Lazy search algorithms can efficiently solve problems where edge evaluation is the bottleneck in computation, as is the case for robotic motion planning. The optimal algorithm in this class, LazySP, lazily restricts edge evaluation to only the shortest path. Doing so comes at the expense of search effort, i.e., LazySP must recompute the search tree every time an edge is found to be invalid. This becomes prohibitively expensive when dealing with large graphs or highly cluttered environments. Our key insight is the need to balance both edge evaluation and search effort to minimize the total planning time. Our contribution is two-fold. First, we propose a framework, Generalized Lazy Search (GLS), that seamlessly toggles between search and evaluation to prevent wasted efforts. We show that for a choice of toggle, GLS is provably more efficient than LazySP. Second, we leverage prior experience of edge probabilities to derive GLS policies that minimize expected planning time. We show that GLS equipped with such priors significantly outperforms competitive baselines for many simulated environments in R2, SE(2) and 7-DoF manipulation.

Sample-Efficient Learning of Nonprehensile Manipulation Policies via Physics-Based Informed State Distributions

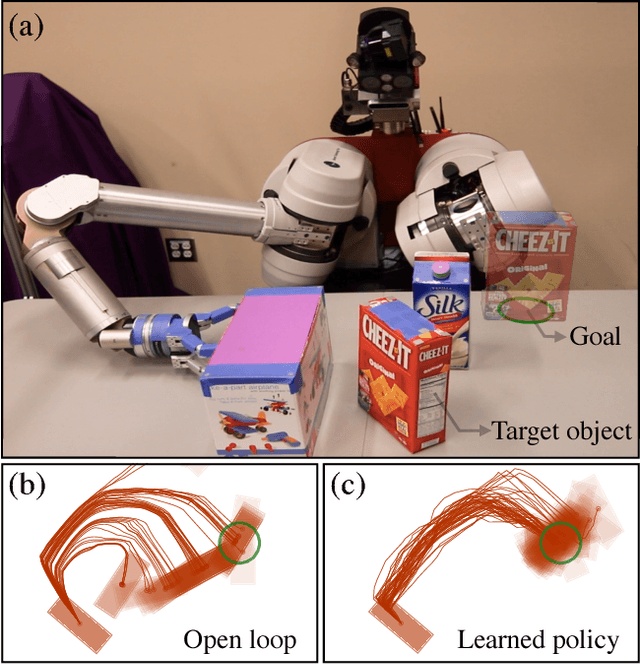
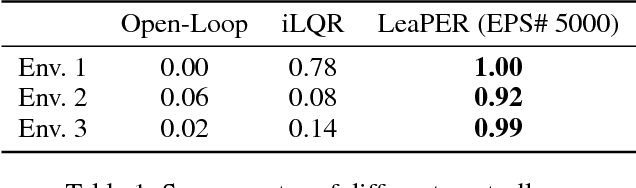
This paper proposes a sample-efficient yet simple approach to learning closed-loop policies for nonprehensile manipulation. Although reinforcement learning (RL) can learn closed-loop policies without requiring access to underlying physics models, it suffers from poor sample complexity on challenging tasks. To overcome this problem, we leverage rearrangement planning to provide an informative physics-based prior on the environment's optimal state-visitation distribution. Specifically, we present a new technique, Learning with Planned Episodic Resets (LeaPER), that resets the environment's state to one informed by the prior during the learning phase. We experimentally show that LeaPER significantly outperforms traditional RL approaches by a factor of up to 5X on simulated rearrangement. Further, we relax dynamics from quasi-static to welded contacts to illustrate that LeaPER is robust to the use of simpler physics models. Finally, LeaPER's closed-loop policies significantly improve task success rates relative to both open-loop controls with a planned path or simple feedback controllers that track open-loop trajectories. We demonstrate the performance and behavior of LeaPER on a physical 7-DOF manipulator in https://youtu.be/feS-zFq6J1c.

Bayesian Policy Optimization for Model Uncertainty

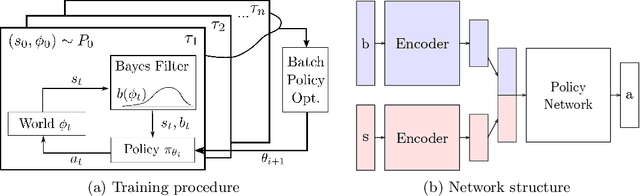
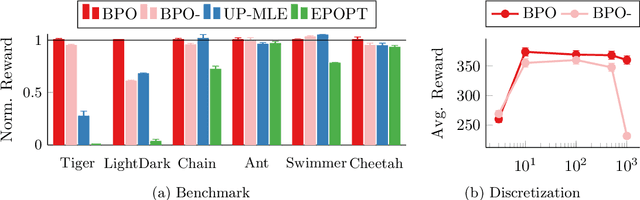
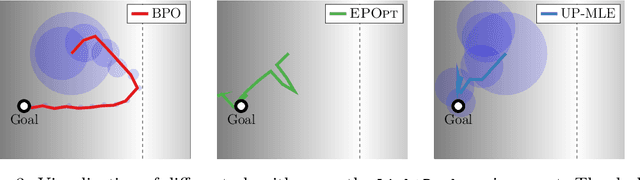
Addressing uncertainty is critical for autonomous systems to robustly adapt to the real world. We formulate the problem of model uncertainty as a continuous Bayes-Adaptive Markov Decision Process (BAMDP), where an agent maintains a posterior distribution over the latent model parameters given a history of observations and maximizes its expected long-term reward with respect to this belief distribution. Our algorithm, Bayesian Policy Optimization, builds on recent policy optimization algorithms to learn a universal policy that navigates the exploration-exploitation trade-off to maximize the Bayesian value function. To address challenges from discretizing the continuous latent parameter space, we propose a policy network architecture that independently encodes the belief distribution from the observable state. Our method significantly outperforms algorithms that address model uncertainty without explicitly reasoning about belief distributions, and is competitive with state-of-the-art Partially Observable Markov Decision Process solvers.

Lazy Receding Horizon A* for Efficient Path Planning in Graphs with Expensive-to-Evaluate Edges

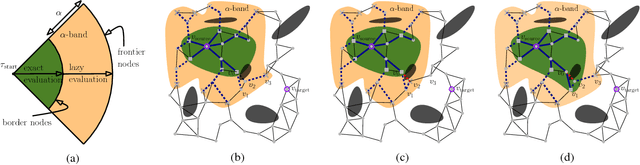
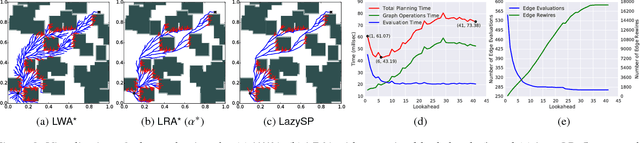
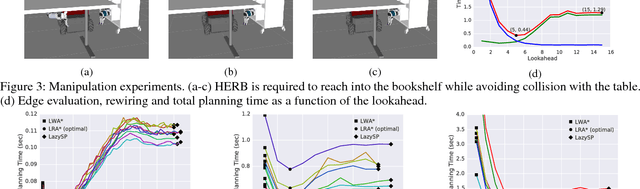
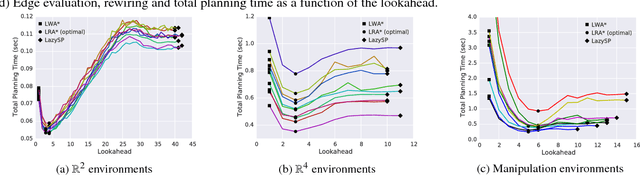
Motion-planning problems, such as manipulation in cluttered environments, often require a collision-free shortest path to be computed quickly given a roadmap graph. Typically, the computational cost of evaluating whether an edge of the roadmap graph is collision-free dominates the running time of search algorithms. Algorithms such as Lazy Weighted A* (LWA*) and LazySP have been proposed to reduce the number of edge evaluations by employing a lazy lookahead (one-step lookahead and infinite-step lookahead, respectively). However, this comes at the expense of additional graph operations: the larger the lookahead, the more the graph operations that are typically required. We propose Lazy Receding-Horizon A* (LRA*) to minimize the total planning time by balancing edge evaluations and graph operations. Endowed with a lazy lookahead, LRA* represents a family of lazy shortest-path graph-search algorithms that generalizes LWA* and LazySP. We analyze the theoretic properties of LRA* and demonstrate empirically that, in many cases, to minimize the total planning time, the algorithm requires an intermediate lazy lookahead. Namely, using an intermediate lazy lookahead, our algorithm outperforms both LWA* and LazySP. These experiments span simulated random worlds in $\mathbb{R}^2$ and $\mathbb{R}^4$, and manipulation problems using a 7-DOF manipulator.