Markov Potential Game with Final-time Reach-Avoid Objectives

We formulate a Markov potential game with final-time reach-avoid objectives by integrating potential game theory with stochastic reach-avoid control. Our focus is on multi-player trajectory planning where players maximize the same multi-player reach-avoid objective: the probability of all participants reaching their designated target states by a specified time, while avoiding collisions with one another. Existing approaches require centralized computation of actions via a global policy, which may have prohibitively expensive communication costs. Instead, we focus on approximations of the global policy via local state feedback policies. First, we adapt the recursive single player reach-avoid value iteration to the multi-player framework with local policies, and show that the same recursion holds on the joint state space. To find each player's optimal local policy, the multi-player reach-avoid value function is projected from the joint state to the local state using the other players' occupancy measures. Then, we propose an iterative best response scheme for the multi-player value iteration to converge to a pure Nash equilibrium. We demonstrate the utility of our approach in finding collision-free policies for multi-player motion planning in simulation.

Projection-free computation of robust controllable sets with constrained zonotopes

We study the problem of computing robust controllable sets for discrete-time linear systems with additive uncertainty. We propose a tractable and scalable approach to inner- and outer-approximate robust controllable sets using constrained zonotopes, when the additive uncertainty set is a symmetric, convex, and compact set. Our least-squares-based approach uses novel closed-form approximations of the Pontryagin difference between a constrained zonotopic minuend and a symmetric, convex, and compact subtrahend. Unlike existing approaches, our approach does not rely on convex optimization solvers, and is projection-free for ellipsoidal and zonotopic uncertainty sets. We also propose a least-squares-based approach to compute a convex, polyhedral outer-approximation to constrained zonotopes, and characterize sufficient conditions under which all these approximations are exact. We demonstrate the computational efficiency and scalability of our approach in several case studies, including the design of abort-safe rendezvous trajectories for a spacecraft in near-rectilinear halo orbit under uncertainty. Our approach can inner-approximate a 20-step robust controllable set for a 100-dimensional linear system in under 15 seconds on a standard computer.

Safe multi-agent motion planning under uncertainty for drones using filtered reinforcement learning

We consider the problem of safe multi-agent motion planning for drones in uncertain, cluttered workspaces. For this problem, we present a tractable motion planner that builds upon the strengths of reinforcement learning and constrained-control-based trajectory planning. First, we use single-agent reinforcement learning to learn motion plans from data that reach the target but may not be collision-free. Next, we use a convex optimization, chance constraints, and set-based methods for constrained control to ensure safety, despite the uncertainty in the workspace, agent motion, and sensing. The proposed approach can handle state and control constraints on the agents, and enforce collision avoidance among themselves and with static obstacles in the workspace with high probability. The proposed approach yields a safe, real-time implementable, multi-agent motion planner that is simpler to train than methods based solely on learning. Numerical simulations and experiments show the efficacy of the approach.

Safely: Safe Stochastic Motion Planning Under Constrained Sensing via Duality

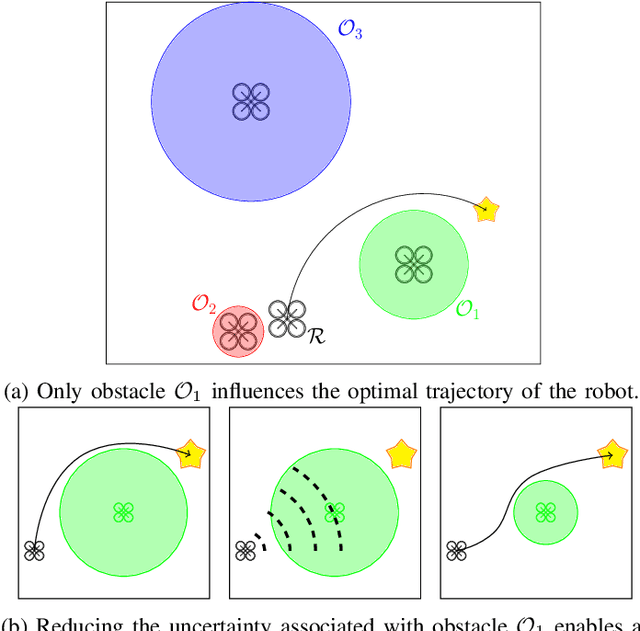
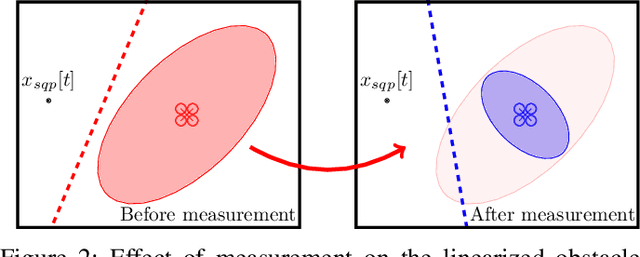
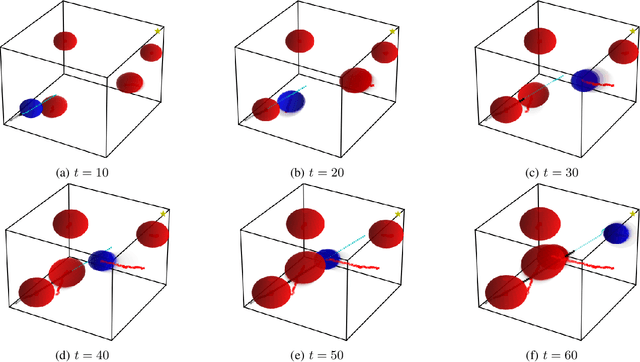
Consider a robot operating in an uncertain environment with stochastic, dynamic obstacles. Despite the clear benefits for trajectory optimization, it is often hard to keep track of each obstacle at every time step due to sensing and hardware limitations. We introduce the Safely motion planner, a receding-horizon control framework, that simultaneously synthesizes both a trajectory for the robot to follow as well as a sensor selection strategy that prescribes trajectory-relevant obstacles to measure at each time step while respecting the sensing constraints of the robot. We perform the motion planning using sequential quadratic programming, and prescribe obstacles to sense based on the duality information associated with the convex subproblems. We guarantee safety by ensuring that the probability of the robot colliding with any of the obstacles is below a prescribed threshold at every time step of the planned robot trajectory. We demonstrate the efficacy of the Safely motion planner through software and hardware experiments.

Physical-Layer Security via Distributed Beamforming in the Presence of Adversaries with Unknown Locations

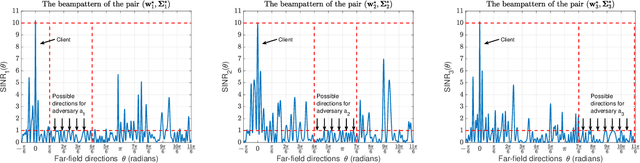
We study the problem of securely communicating a sequence of information bits with a client in the presence of multiple adversaries at unknown locations in the environment. We assume that the client and the adversaries are located in the far-field region, and all possible directions for each adversary can be expressed as a continuous interval of directions. In such a setting, we develop a periodic transmission strategy, i.e., a sequence of joint beamforming gain and artificial noise pairs, that prevents the adversaries from decreasing their uncertainty on the information sequence by eavesdropping on the transmission. We formulate a series of nonconvex semi-infinite optimization problems to synthesize the transmission strategy. We show that the semi-definite program (SDP) relaxations of these nonconvex problems are exact under an efficiently verifiable sufficient condition. We approximate the SDP relaxations, which are subject to infinitely many constraints, by randomly sampling a finite subset of the constraints and establish the probability with which optimal solutions to the obtained finite SDPs and the semi-infinite SDPs coincide. We demonstrate with numerical simulations that the proposed periodic strategy can ensure the security of communication in scenarios in which all stationary strategies fail to guarantee security.

Near-Optimal Reactive Synthesis Incorporating Runtime Information

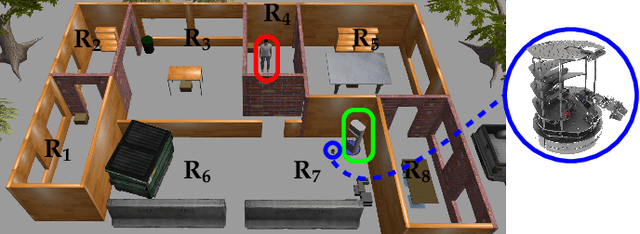
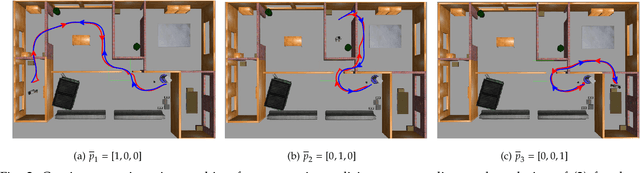
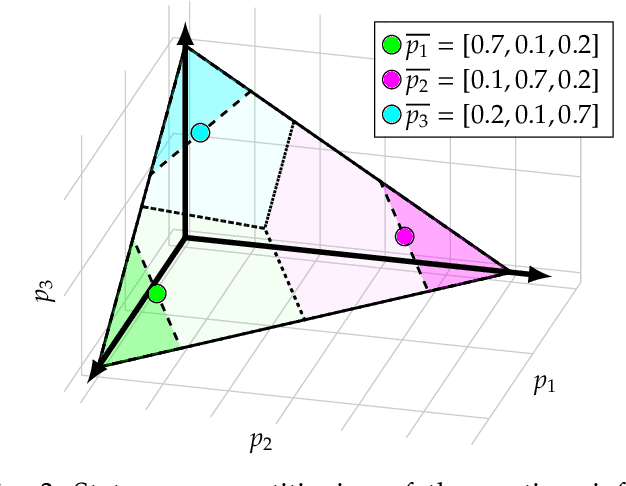
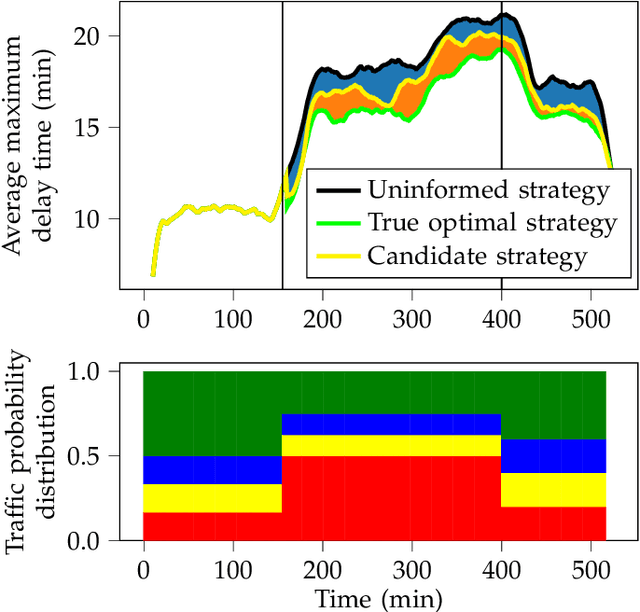
We consider the problem of optimal reactive synthesis - compute a strategy that satisfies a mission specification in a dynamic environment, and optimizes a performance metric. We incorporate task-critical information, that is only available at runtime, into the strategy synthesis in order to improve performance. Existing approaches to utilising such time-varying information require online re-synthesis, which is not computationally feasible in real-time applications. In this paper, we pre-synthesize a set of strategies corresponding to candidate instantiations (pre-specified representative information scenarios). We then propose a novel switching mechanism to dynamically switch between the strategies at runtime while guaranteeing all safety and liveness goals are met. We also characterize bounds on the performance suboptimality. We demonstrate our approach on two examples - robotic motion planning where the likelihood of the position of the robot's goal is updated in real-time, and an air traffic management problem for urban air mobility.