Scalable and transferable learning of algorithms via graph embedding for multi-robot reward collection

Can the success of reinforcement learning methods for combinatorial optimization problems be extended to multi-robot scheduling problems in stochastic contexts? Three issues are particularly important in this context: quality of the resulting decisions, scalability, and transferability. To achieve these ends we generalize the concept of clique potential to stochastic clique potential. We extend a mean field inference fixed point iteration with this new concept and use it to modify thestructure2vec method. We next propose a new reinforcement learning framework combining a graph representation of the problem and a consensus auction inspired by heuristics in the problem domain. This representation enables transferability in terms of the number of robots. Sequential encoding of information through multiple layers of our extended structure2vec results in 96% optimal performance of the learned heuristics. While training tractability is inherited from single robot methods in the literature, use of a multi-robot consensus auction-based relaxation of the maximum operation in the Bellman optimality equation allows for scalable selection of actions in the fitted Q-iteration. We apply our framework to multi-robot reward collection (MRRC) problems in stochastic environments with linear or non-linear rewards. In stochastic environments with non-linear rewards, the new method achieves 20% superior performance relative to the popular sequential greedy assignment (SGA) algorithm. Linear scalability in terms of training is achieved and demonstrated. Transferability is demonstrated by the use of a heuristic trained with three robots that continues to achieve 95% optimal performance when applied to problems with various numbers of robots. We further mention the results obtained when extending the approach to identical parallel machine scheduling(IPMS) problems.

Feature Propagation on Graph: A New Perspective to Graph Representation Learning

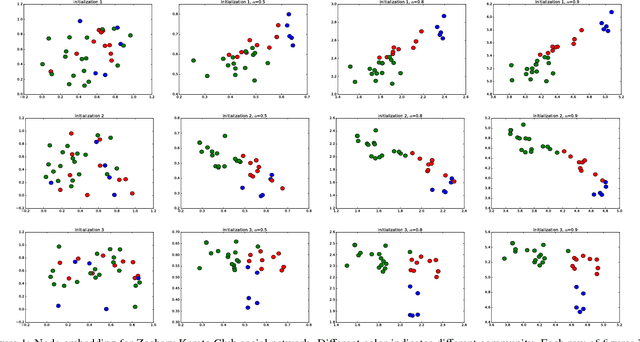
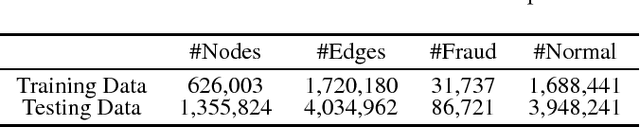
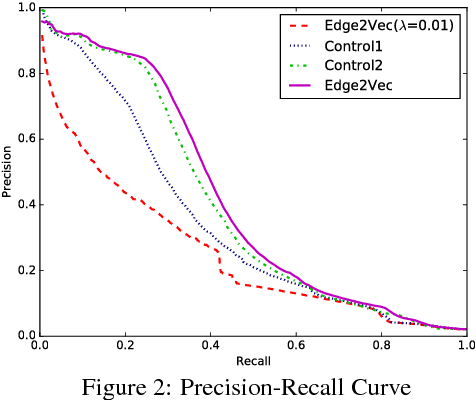
We study feature propagation on graph, an inference process involved in graph representation learning tasks. It's to spread the features over the whole graph to the $t$-th orders, thus to expand the end's features. The process has been successfully adopted in graph embedding or graph neural networks, however few works studied the convergence of feature propagation. Without convergence guarantees, it may lead to unexpected numerical overflows and task failures. In this paper, we first define the concept of feature propagation on graph formally, and then study its convergence conditions to equilibrium states. We further link feature propagation to several established approaches such as node2vec and structure2vec. In the end of this paper, we extend existing approaches from represent nodes to edges (edge2vec) and demonstrate its applications on fraud transaction detection in real world scenario. Experiments show that it is quite competitive.

Discriminative Embeddings of Latent Variable Models for Structured Data

Kernel classifiers and regressors designed for structured data, such as sequences, trees and graphs, have significantly advanced a number of interdisciplinary areas such as computational biology and drug design. Typically, kernels are designed beforehand for a data type which either exploit statistics of the structures or make use of probabilistic generative models, and then a discriminative classifier is learned based on the kernels via convex optimization. However, such an elegant two-stage approach also limited kernel methods from scaling up to millions of data points, and exploiting discriminative information to learn feature representations. We propose, structure2vec, an effective and scalable approach for structured data representation based on the idea of embedding latent variable models into feature spaces, and learning such feature spaces using discriminative information. Interestingly, structure2vec extracts features by performing a sequence of function mappings in a way similar to graphical model inference procedures, such as mean field and belief propagation. In applications involving millions of data points, we showed that structure2vec runs 2 times faster, produces models which are $10,000$ times smaller, while at the same time achieving the state-of-the-art predictive performance.