Sampling from Energy distributions with Target Concrete Score Identity

We introduce the Target Concrete Score Identity Sampler (TCSIS), a method for sampling from unnormalized densities on discrete state spaces by learning the reverse dynamics of a Continuous-Time Markov Chain (CTMC). Our approach builds on a forward in time CTMC with a uniform noising kernel and relies on the proposed Target Concrete Score Identity, which relates the concrete score, the ratio of marginal probabilities of two states, to a ratio of expectations of Boltzmann factors under the forward uniform diffusion kernel. This formulation enables Monte Carlo estimation of the concrete score without requiring samples from the target distribution or computation of the partition function. We approximate the concrete score with a neural network and propose two algorithms: Self-Normalized TCSIS and Unbiased TCSIS. Finally, we demonstrate the effectiveness of TCSIS on problems from statistical physics.

Neural Logistic Bandits

We study the problem of neural logistic bandits, where the main task is to learn an unknown reward function within a logistic link function using a neural network. Existing approaches either exhibit unfavorable dependencies on $\kappa$, where $1/\kappa$ represents the minimum variance of reward distributions, or suffer from direct dependence on the feature dimension $d$, which can be huge in neural network-based settings. In this work, we introduce a novel Bernstein-type inequality for self-normalized vector-valued martingales that is designed to bypass a direct dependence on the ambient dimension. This lets us deduce a regret upper bound that grows with the effective dimension $\widetilde{d}$, not the feature dimension, while keeping a minimal dependence on $\kappa$. Based on the concentration inequality, we propose two algorithms, NeuralLog-UCB-1 and NeuralLog-UCB-2, that guarantee regret upper bounds of order $\widetilde{O}(\widetilde{d}\sqrt{\kappa T})$ and $\widetilde{O}(\widetilde{d}\sqrt{T/\kappa})$, respectively, improving on the existing results. Lastly, we report numerical results on both synthetic and real datasets to validate our theoretical findings.

Self-Normalized Resets for Plasticity in Continual Learning

Plasticity Loss is an increasingly important phenomenon that refers to the empirical observation that as a neural network is continually trained on a sequence of changing tasks, its ability to adapt to a new task diminishes over time. We introduce Self-Normalized Resets (SNR), a simple adaptive algorithm that mitigates plasticity loss by resetting a neuron's weights when evidence suggests its firing rate has effectively dropped to zero. Across a battery of continual learning problems and network architectures, we demonstrate that SNR consistently attains superior performance compared to its competitor algorithms. We also demonstrate that SNR is robust to its sole hyperparameter, its rejection percentile threshold, while competitor algorithms show significant sensitivity. SNR's threshold-based reset mechanism is motivated by a simple hypothesis test that we derive. Seen through the lens of this hypothesis test, competing reset proposals yield suboptimal error rates in correctly detecting inactive neurons, potentially explaining our experimental observations. We also conduct a theoretical investigation of the optimization landscape for the problem of learning a single ReLU. We show that even when initialized adversarially, an idealized version of SNR learns the target ReLU, while regularization-based approaches can fail to learn.

SeNMo: A Self-Normalizing Deep Learning Model for Enhanced Multi-Omics Data Analysis in Oncology

Multi-omics research has enhanced our understanding of cancer heterogeneity and progression. Investigating molecular data through multi-omics approaches is crucial for unraveling the complex biological mechanisms underlying cancer, thereby enabling effective diagnosis, treatment, and prevention strategies. However, predicting patient outcomes through integration of all available multi-omics data is an under-study research direction. Here, we present SeNMo (Self-normalizing Network for Multi-omics), a deep neural network trained on multi-omics data across 33 cancer types. SeNMo is efficient in handling multi-omics data characterized by high-width (many features) and low-length (fewer samples) attributes. We trained SeNMo for the task of overall survival using pan-cancer data involving 33 cancer sites from Genomics Data Commons (GDC). The training data includes gene expression, DNA methylation, miRNA expression, DNA mutations, protein expression modalities, and clinical data. We evaluated the model's performance in predicting overall survival using concordance index (C-Index). SeNMo performed consistently well in training regime, with the validation C-Index of 0.76 on GDC's public data. In the testing regime, SeNMo performed with a C-Index of 0.758 on a held-out test set. The model showed an average accuracy of 99.8% on the task of classifying the primary cancer type on the pan-cancer test cohort. SeNMo proved to be a mini-foundation model for multi-omics oncology data because it demonstrated robust performance, and adaptability not only across molecular data types but also on the classification task of predicting the primary cancer type of patients. SeNMo can be further scaled to any cancer site and molecular data type. We believe SeNMo and similar models are poised to transform the oncology landscape, offering hope for more effective, efficient, and patient-centric cancer care.

Self-Normalizing Neural Network, Enabling One Shot Transfer Learning for Modeling EDFA Wavelength Dependent Gain

We present a novel ML framework for modeling the wavelength-dependent gain of multiple EDFAs, based on semi-supervised, self-normalizing neural networks, enabling one-shot transfer learning. Our experiments on 22 EDFAs in Open Ireland and COSMOS testbeds show high-accuracy transfer-learning even when operated across different amplifier types.

GNN-VPA: A Variance-Preserving Aggregation Strategy for Graph Neural Networks

Graph neural networks (GNNs), and especially message-passing neural networks, excel in various domains such as physics, drug discovery, and molecular modeling. The expressivity of GNNs with respect to their ability to discriminate non-isomorphic graphs critically depends on the functions employed for message aggregation and graph-level readout. By applying signal propagation theory, we propose a variance-preserving aggregation function (VPA) that maintains expressivity, but yields improved forward and backward dynamics. Experiments demonstrate that VPA leads to increased predictive performance for popular GNN architectures as well as improved learning dynamics. Our results could pave the way towards normalizer-free or self-normalizing GNNs.

Energy-Based Models with Applications to Speech and Language Processing

Energy-Based Models (EBMs) are an important class of probabilistic models, also known as random fields and undirected graphical models. EBMs are un-normalized and thus radically different from other popular self-normalized probabilistic models such as hidden Markov models (HMMs), autoregressive models, generative adversarial nets (GANs) and variational auto-encoders (VAEs). Over the past years, EBMs have attracted increasing interest not only from the core machine learning community, but also from application domains such as speech, vision, natural language processing (NLP) and so on, due to significant theoretical and algorithmic progress. The sequential nature of speech and language also presents special challenges and needs a different treatment from processing fix-dimensional data (e.g., images). Therefore, the purpose of this monograph is to present a systematic introduction to energy-based models, including both algorithmic progress and applications in speech and language processing. First, the basics of EBMs are introduced, including classic models, recent models parameterized by neural networks, sampling methods, and various learning methods from the classic learning algorithms to the most advanced ones. Then, the application of EBMs in three different scenarios is presented, i.e., for modeling marginal, conditional and joint distributions, respectively. 1) EBMs for sequential data with applications in language modeling, where the main focus is on the marginal distribution of a sequence itself; 2) EBMs for modeling conditional distributions of target sequences given observation sequences, with applications in speech recognition, sequence labeling and text generation; 3) EBMs for modeling joint distributions of both sequences of observations and targets, and their applications in semi-supervised learning and calibrated natural language understanding.

Deep learning for diffusion in porous media

We adopt convolutional neural networks (CNN) to predict the basic properties of the porous media. Two different media types are considered: one mimics the sandstone, and the other mimics the systems derived from the extracellular space of biological tissues. The Lattice Boltzmann Method is used to obtain the labeled data necessary for performing supervised learning. We distinguish two tasks. In the first, networks based on the analysis of the system's geometry predict porosity and effective diffusion coefficient. In the second, networks reconstruct the system's geometry and concentration map. In the first task, we propose two types of CNN models: the C-Net and the encoder part of the U-Net. Both networks are modified by adding a self-normalization module. The models predict with reasonable accuracy but only within the data type, they are trained on. For instance, the model trained on sandstone-like samples overshoots or undershoots for biological-like samples. In the second task, we propose the usage of the U-Net architecture. It accurately reconstructs the concentration fields. Moreover, the network trained on one data type works well for the other. For instance, the model trained on sandstone-like samples works perfectly on biological-like samples.

More layers! End-to-end regression and uncertainty on tabular data with deep learning

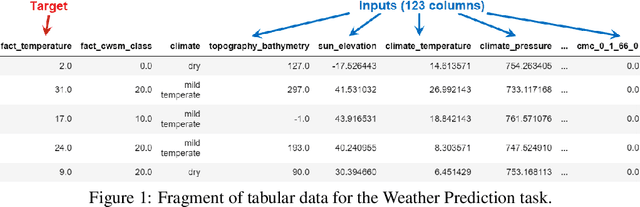
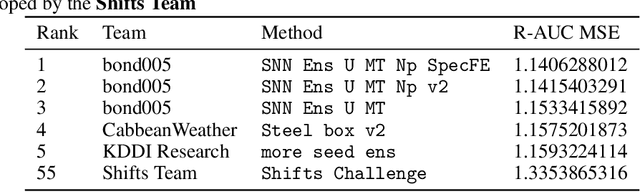
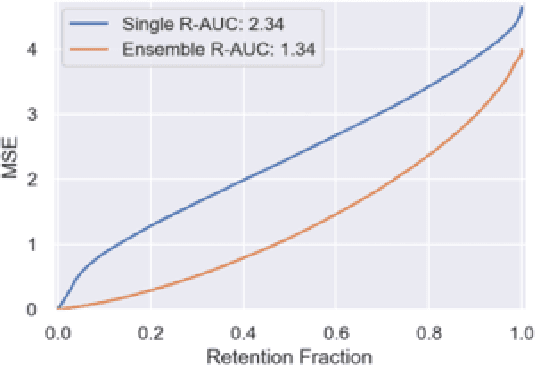
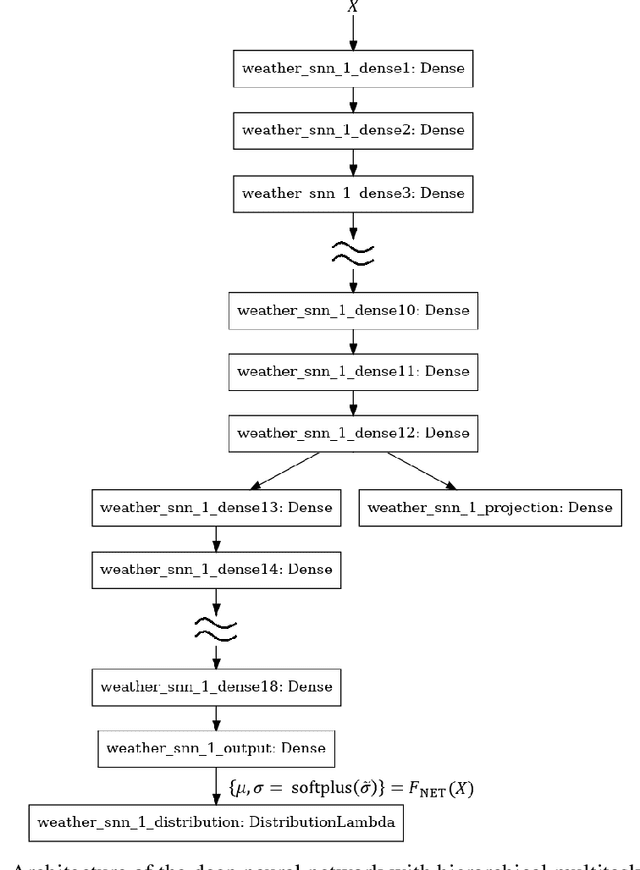
This paper attempts to analyze the effectiveness of deep learning for tabular data processing. It is believed that decision trees and their ensembles is the leading method in this domain, and deep neural networks must be content with computer vision and so on. But the deep neural network is a framework for building gradient-based hierarchical representations, and this key feature should be able to provide the best processing of generic structured (tabular) data, not just image matrices and audio spectrograms. This problem is considered through the prism of the Weather Prediction track in the Yandex Shifts challenge (in other words, the Yandex Shifts Weather task). This task is a variant of the classical tabular data regression problem. It is also connected with another important problem: generalization and uncertainty in machine learning. This paper proposes an end-to-end algorithm for solving the problem of regression with uncertainty on tabular data, which is based on the combination of four ideas: 1) deep ensemble of self-normalizing neural networks, 2) regression as parameter estimation of the Gaussian target error distribution, 3) hierarchical multitask learning, and 4) simple data preprocessing. Three modifications of the proposed algorithm form the top-3 leaderboard of the Yandex Shifts Weather challenge respectively. This paper considers that this success has occurred due to the fundamental properties of the deep learning algorithm, and tries to prove this.

Self-Normalized Density Map (SNDM) for Counting Microbiological Objects

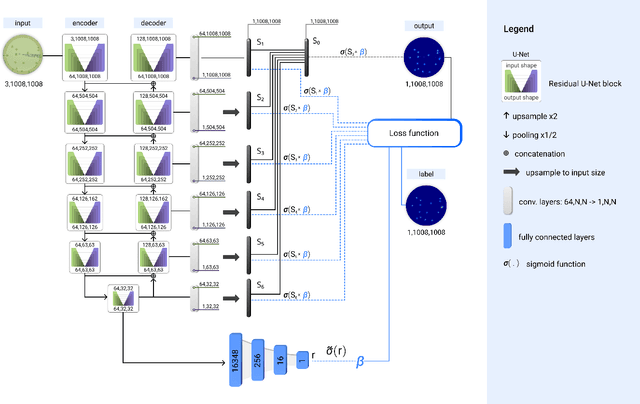
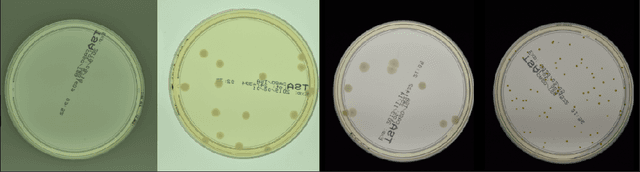
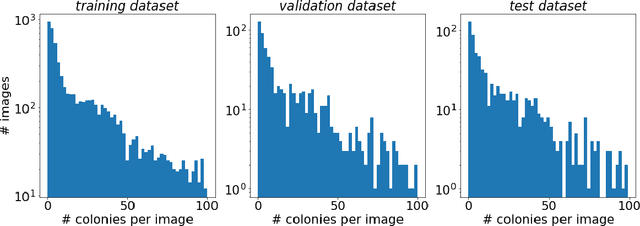
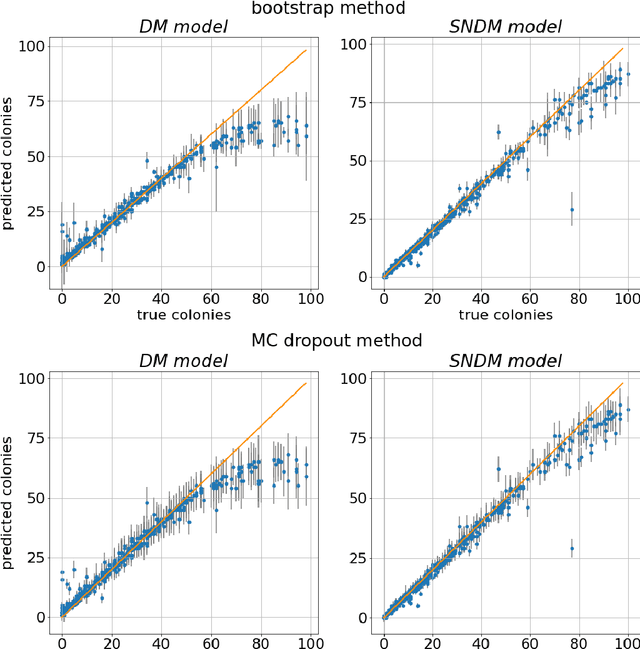
The statistical properties of the density map (DM) approach to counting microbiological objects on images are studied in detail. The DM is given by U$^2$-Net. Two statistical methods for deep neural networks are utilized: the bootstrap and the Monte Carlo (MC) dropout. The detailed analysis of the uncertainties for the DM predictions leads to a deeper understanding of the DM model's deficiencies. Based on our investigation, we propose a self-normalization module in the network. The improved network model, called Self-Normalized Density Map (SNDM), can correct its output density map by itself to accurately predict the total number of objects in the image. The SNDM architecture outperforms the original model. Moreover, both statistical frameworks -- bootstrap and MC dropout -- have consistent statistical results for SNDM, which were not observed in the original model.