Extragradient Type Methods for Riemannian Variational Inequality Problems

Riemannian convex optimization and minimax optimization have recently drawn considerable attention. Their appeal lies in their capacity to adeptly manage the non-convexity of the objective function as well as constraints inherent in the feasible set in the Euclidean sense. In this work, we delve into monotone Riemannian Variational Inequality Problems (RVIPs), which encompass both Riemannian convex optimization and minimax optimization as particular cases. In the context of Euclidean space, it is established that the last-iterates of both the extragradient (EG) and past extragradient (PEG) methods converge to the solution of monotone variational inequality problems at a rate of $O\left(\frac{1}{\sqrt{T}}\right)$ (Cai et al., 2022). However, analogous behavior on Riemannian manifolds remains an open question. To bridge this gap, we introduce the Riemannian extragradient (REG) and Riemannian past extragradient (RPEG) methods. We demonstrate that both exhibit $O\left(\frac{1}{\sqrt{T}}\right)$ last-iterate convergence. Additionally, we show that the average-iterate convergence of both REG and RPEG is $O\left(\frac{1}{{T}}\right)$, aligning with observations in the Euclidean case (Mokhtari et al., 2020). These results are enabled by judiciously addressing the holonomy effect so that additional complications in Riemannian cases can be reduced and the Euclidean proof inspired by the performance estimation problem (PEP) technique or the sum-of-squares (SOS) technique can be applied again.

Randomized Quantization is All You Need for Differential Privacy in Federated Learning

Federated learning (FL) is a common and practical framework for learning a machine model in a decentralized fashion. A primary motivation behind this decentralized approach is data privacy, ensuring that the learner never sees the data of each local source itself. Federated learning then comes with two majors challenges: one is handling potentially complex model updates between a server and a large number of data sources; the other is that de-centralization may, in fact, be insufficient for privacy, as the local updates themselves can reveal information about the sources' data. To address these issues, we consider an approach to federated learning that combines quantization and differential privacy. Absent privacy, Federated Learning often relies on quantization to reduce communication complexity. We build upon this approach and develop a new algorithm called the \textbf{R}andomized \textbf{Q}uantization \textbf{M}echanism (RQM), which obtains privacy through a two-levels of randomization. More precisely, we randomly sub-sample feasible quantization levels, then employ a randomized rounding procedure using these sub-sampled discrete levels. We are able to establish that our results preserve ``Renyi differential privacy'' (Renyi DP). We empirically study the performance of our algorithm and demonstrate that compared to previous work it yields improved privacy-accuracy trade-offs for DP federated learning. To the best of our knowledge, this is the first study that solely relies on randomized quantization without incorporating explicit discrete noise to achieve Renyi DP guarantees in Federated Learning systems.

On Riemannian Projection-free Online Learning

The projection operation is a critical component in a wide range of optimization algorithms, such as online gradient descent (OGD), for enforcing constraints and achieving optimal regret bounds. However, it suffers from computational complexity limitations in high-dimensional settings or when dealing with ill-conditioned constraint sets. Projection-free algorithms address this issue by replacing the projection oracle with more efficient optimization subroutines. But to date, these methods have been developed primarily in the Euclidean setting, and while there has been growing interest in optimization on Riemannian manifolds, there has been essentially no work in trying to utilize projection-free tools here. An apparent issue is that non-trivial affine functions are generally non-convex in such domains. In this paper, we present methods for obtaining sub-linear regret guarantees in online geodesically convex optimization on curved spaces for two scenarios: when we have access to (a) a separation oracle or (b) a linear optimization oracle. For geodesically convex losses, and when a separation oracle is available, our algorithms achieve $O(T^{1/2}\:)$ and $O(T^{3/4}\;)$ adaptive regret guarantees in the full information setting and the bandit setting, respectively. When a linear optimization oracle is available, we obtain regret rates of $O(T^{3/4}\;)$ for geodesically convex losses and $O(T^{2/3}\; log T )$ for strongly geodesically convex losses

Faster Margin Maximization Rates for Generic Optimization Methods

First-order optimization methods tend to inherently favor certain solutions over others when minimizing a given training objective with multiple local optima. This phenomenon, known as implicit bias, plays a critical role in understanding the generalization capabilities of optimization algorithms. Recent research has revealed that gradient-descent-based methods exhibit an implicit bias for the $\ell_2$-maximal margin classifier in the context of separable binary classification. In contrast, generic optimization methods, such as mirror descent and steepest descent, have been shown to converge to maximal margin classifiers defined by alternative geometries. However, while gradient-descent-based algorithms demonstrate fast implicit bias rates, the implicit bias rates of generic optimization methods have been relatively slow. To address this limitation, in this paper, we present a series of state-of-the-art implicit bias rates for mirror descent and steepest descent algorithms. Our primary technique involves transforming a generic optimization algorithm into an online learning dynamic that solves a regularized bilinear game, providing a unified framework for analyzing the implicit bias of various optimization methods. The accelerated rates are derived leveraging the regret bounds of online learning algorithms within this game framework.

Minimizing Dynamic Regret on Geodesic Metric Spaces

In this paper, we consider the sequential decision problem where the goal is to minimize the general dynamic regret on a complete Riemannian manifold. The task of offline optimization on such a domain, also known as a geodesic metric space, has recently received significant attention. The online setting has received significantly less attention, and it has remained an open question whether the body of results that hold in the Euclidean setting can be transplanted into the land of Riemannian manifolds where new challenges (e.g., curvature) come into play. In this paper, we show how to get optimistic regret bound on manifolds with non-positive curvature whenever improper learning is allowed and propose an array of adaptive no-regret algorithms. To the best of our knowledge, this is the first work that considers general dynamic regret and develops "optimistic" online learning algorithms which can be employed on geodesic metric spaces.

Adaptive Oracle-Efficient Online Learning

The classical algorithms for online learning and decision-making have the benefit of achieving the optimal performance guarantees, but suffer from computational complexity limitations when implemented at scale. More recent sophisticated techniques, which we refer to as oracle-efficient methods, address this problem by dispatching to an offline optimization oracle that can search through an exponentially-large (or even infinite) space of decisions and select that which performed the best on any dataset. But despite the benefits of computational feasibility, oracle-efficient algorithms exhibit one major limitation: while performing well in worst-case settings, they do not adapt well to friendly environments. In this paper we consider two such friendly scenarios, (a) "small-loss" problems and (b) IID data. We provide a new framework for designing follow-the-perturbed-leader algorithms that are oracle-efficient and adapt well to the small-loss environment, under a particular condition which we call approximability (which is spiritually related to sufficient conditions provided by Dud\'{i}k et al., [2020]). We identify a series of real-world settings, including online auctions and transductive online classification, for which approximability holds. We also extend the algorithm to an IID data setting and establish a "best-of-both-worlds" bound in the oracle-efficient setting.

Supervised Hashing based on Energy Minimization

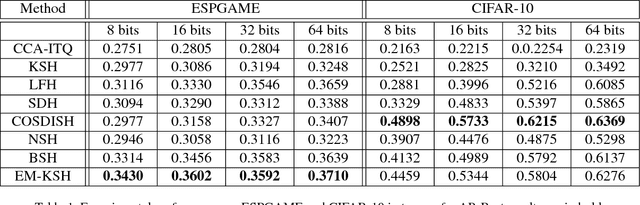
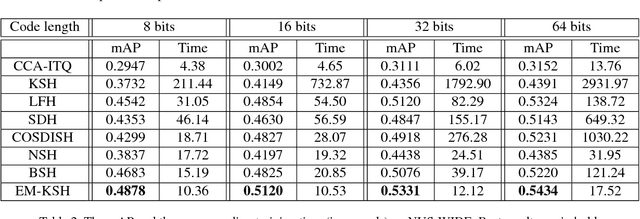
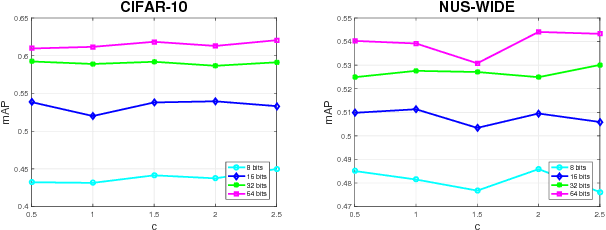
Recently, supervised hashing methods have attracted much attention since they can optimize retrieval speed and storage cost while preserving semantic information. Because hashing codes learning is NP-hard, many methods resort to some form of relaxation technique. But the performance of these methods can easily deteriorate due to the relaxation. Luckily, many supervised hashing formulations can be viewed as energy functions, hence solving hashing codes is equivalent to learning marginals in the corresponding conditional random field (CRF). By minimizing the KL divergence between a fully factorized distribution and the Gibbs distribution of this CRF, a set of consistency equations can be obtained, but updating them in parallel may not yield a local optimum since the variational lower bound is not guaranteed to increase. In this paper, we use a linear approximation of the sigmoid function to convert these consistency equations to linear systems, which have a closed-form solution. By applying this novel technique to two classical hashing formulations KSH and SPLH, we obtain two new methods called EM (energy minimizing based)-KSH and EM-SPLH. Experimental results on three datasets show the superiority of our methods.