HAWQ-V2: Hessian Aware trace-Weighted Quantization of Neural Networks

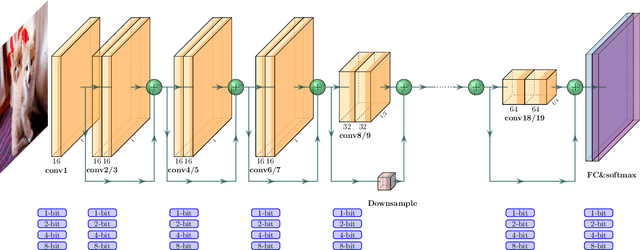
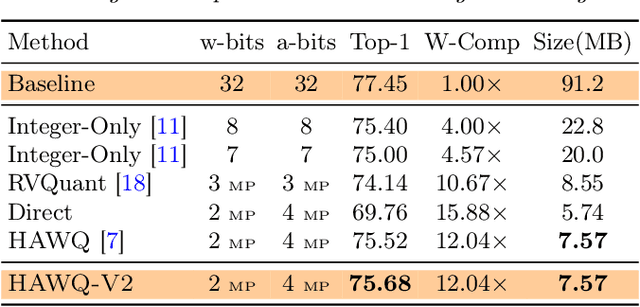
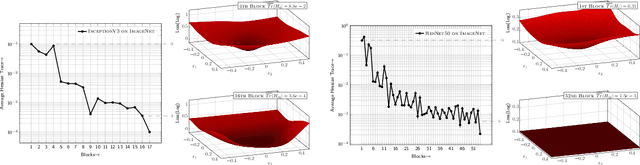
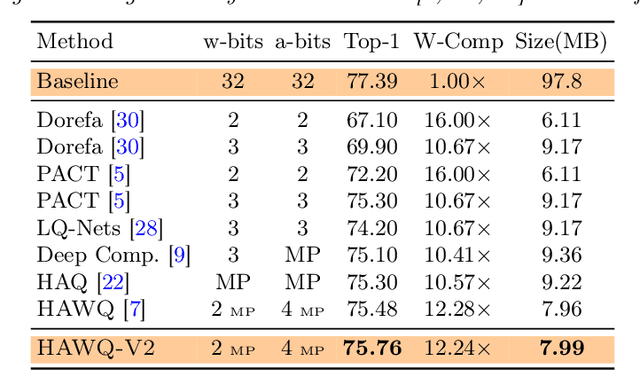
Quantization is an effective method for reducing memory footprint and inference time of Neural Networks, e.g., for efficient inference in the cloud, especially at the edge. However, ultra low precision quantization could lead to significant degradation in model generalization. A promising method to address this is to perform mixed-precision quantization, where more sensitive layers are kept at higher precision. However, the search space for a mixed-precision quantization is exponential in the number of layers. Recent work has proposed HAWQ, a novel Hessian based framework, with the aim of reducing this exponential search space by using second-order information. While promising, this prior work has three major limitations: (i) HAWQV1 only uses the top Hessian eigenvalue as a measure of sensitivity and do not consider the rest of the Hessian spectrum; (ii) HAWQV1 approach only provides relative sensitivity of different layers and therefore requires a manual selection of the mixed-precision setting; and (iii) HAWQV1 does not consider mixed-precision activation quantization. Here, we present HAWQV2 which addresses these shortcomings. For (i), we perform a theoretical analysis showing that a better sensitivity metric is to compute the average of all of the Hessian eigenvalues. For (ii), we develop a Pareto frontier based method for selecting the exact bit precision of different layers without any manual selection. For (iii), we extend the Hessian analysis to mixed-precision activation quantization. We have found this to be very beneficial for object detection. We show that HAWQV2 achieves new state-of-the-art results for a wide range of tasks.

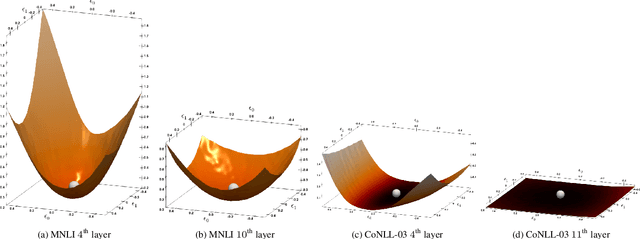
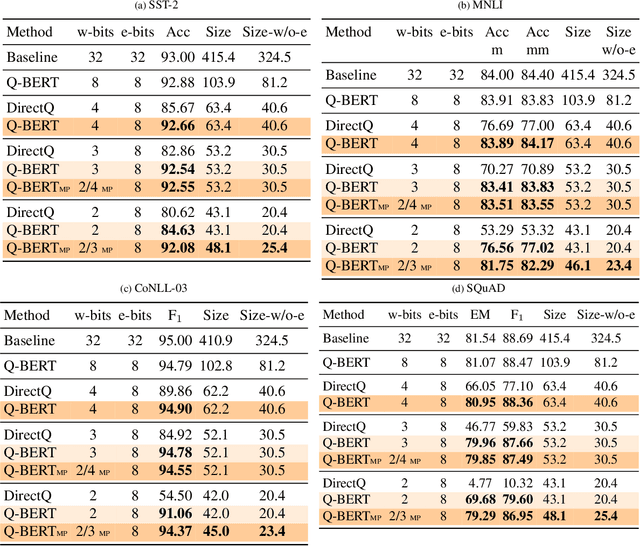
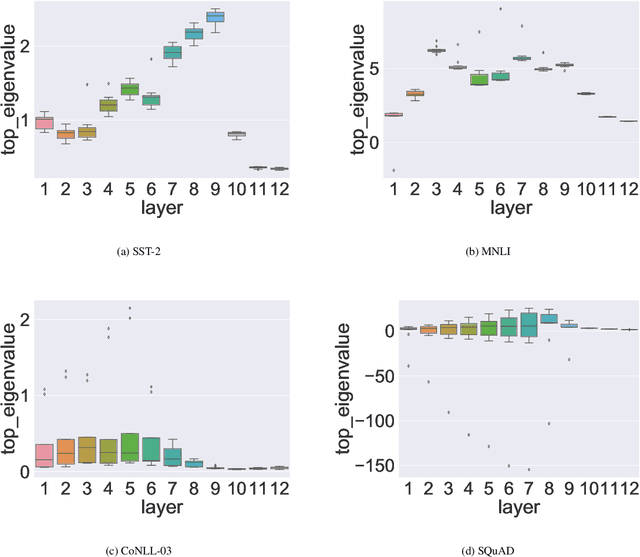
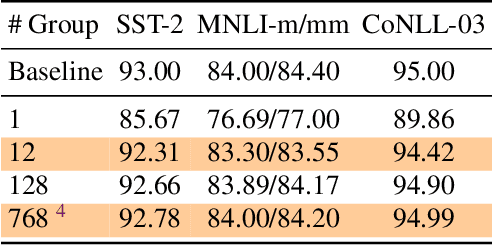
Q-BERT: Hessian Based Ultra Low Precision Quantization of BERT

Transformer based architectures have become de-facto models used for a range of Natural Language Processing tasks. In particular, the BERT based models achieved significant accuracy gain for GLUE tasks, CoNLL-03 and SQuAD. However, BERT based models have a prohibitive memory footprint and latency. As a result, deploying BERT based models in resource constrained environments has become a challenging task. In this work, we perform an extensive analysis of fine-tuned BERT models using second order Hessian information, and we use our results to propose a novel method for quantizing BERT models to ultra low precision. In particular, we propose a new group-wise quantization scheme, and we use a Hessian based mix-precision method to compress the model further. We extensively test our proposed method on BERT downstream tasks of SST-2, MNLI, CoNLL-03, and SQuAD. We can achieve comparable performance to baseline with at most $2.3\%$ performance degradation, even with ultra-low precision quantization down to 2 bits, corresponding up to $13\times$ compression of the model parameters, and up to $4\times$ compression of the embedding table as well as activations. Among all tasks, we observed the highest performance loss for BERT fine-tuned on SQuAD. By probing into the Hessian based analysis as well as visualization, we show that this is related to the fact that current training/fine-tuning strategy of BERT does not converge for SQuAD.

ANODEV2: A Coupled Neural ODE Evolution Framework

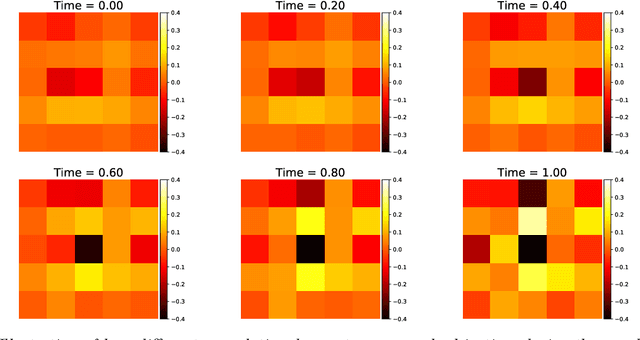
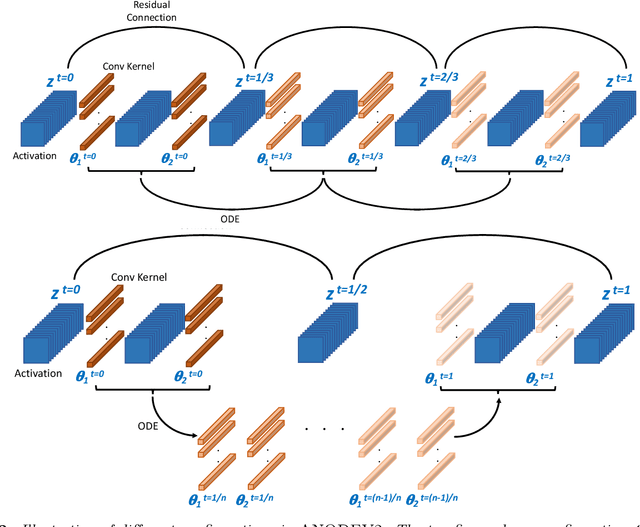
It has been observed that residual networks can be viewed as the explicit Euler discretization of an Ordinary Differential Equation (ODE). This observation motivated the introduction of so-called Neural ODEs, which allow more general discretization schemes with adaptive time stepping. Here, we propose ANODEV2, which is an extension of this approach that also allows evolution of the neural network parameters, in a coupled ODE-based formulation. The Neural ODE method introduced earlier is in fact a special case of this new more general framework. We present the formulation of ANODEV2, derive optimality conditions, and implement a coupled reaction-diffusion-advection version of this framework in PyTorch. We present empirical results using several different configurations of ANODEV2, testing them on multiple models on CIFAR-10. We report results showing that this coupled ODE-based framework is indeed trainable, and that it achieves higher accuracy, as compared to the baseline models as well as the recently-proposed Neural ODE approach.

Residual Networks as Nonlinear Systems: Stability Analysis using Linearization

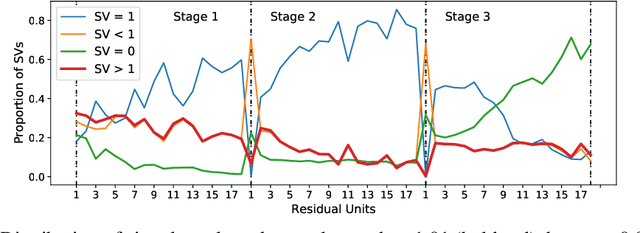
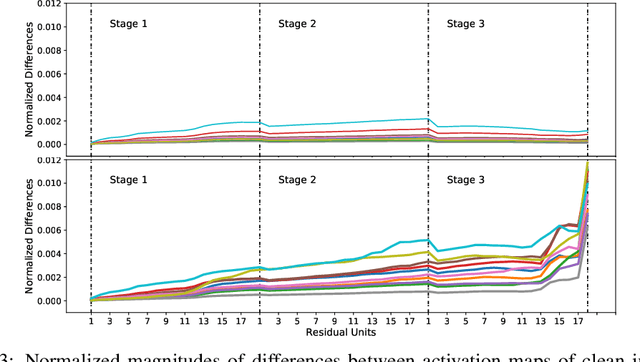
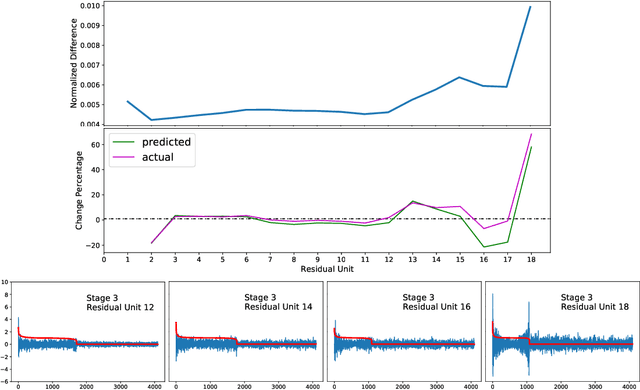
We regard pre-trained residual networks (ResNets) as nonlinear systems and use linearization, a common method used in the qualitative analysis of nonlinear systems, to understand the behavior of the networks under small perturbations of the input images. We work with ResNet-56 and ResNet-110 trained on the CIFAR-10 data set. We linearize these networks at the level of residual units and network stages, and the singular value decomposition is used in the stability analysis of these components. It is found that most of the singular values of the linearizations of residual units are 1 and, in spite of the fact that the linearizations depend directly on the activation maps, the singular values differ only slightly for different input images. However, adjusting the scaling of the skip connection or the values of the weights in a residual unit has a significant impact on the singular value distributions. Inspection of how random and adversarial perturbations of input images propagate through the network reveals that there is a dramatic jump in the magnitude of adversarial perturbations towards the end of the final stage of the network that is not present in the case of random perturbations. We attempt to gain a better understanding of this phenomenon by projecting the perturbations onto singular vectors of the linearizations of the residual units.

HAWQ: Hessian AWare Quantization of Neural Networks with Mixed-Precision

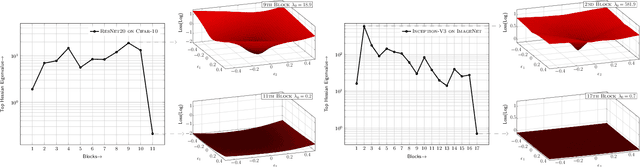
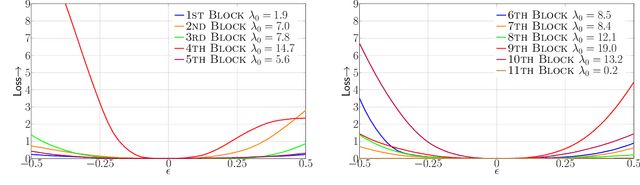
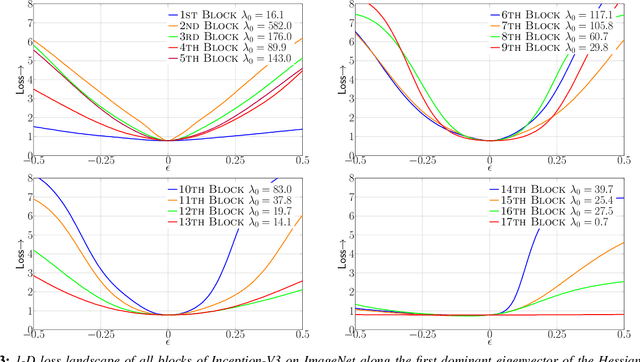
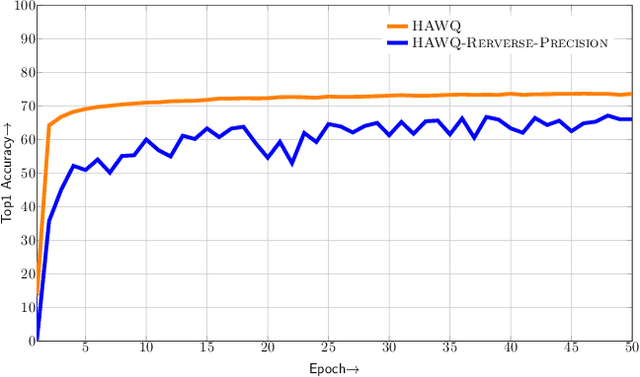
Model size and inference speed/power have become a major challenge in the deployment of Neural Networks for many applications. A promising approach to address these problems is quantization. However, uniformly quantizing a model to ultra low precision leads to significant accuracy degradation. A novel solution for this is to use mixed-precision quantization, as some parts of the network may allow lower precision as compared to other layers. However, there is no systematic way to determine the precision of different layers. A brute force approach is not feasible for deep networks, as the search space for mixed-precision is exponential in the number of layers. Another challenge is a similar factorial complexity for determining block-wise fine-tuning order when quantizing the model to a target precision. Here, we introduce Hessian AWare Quantization (HAWQ), a novel second-order quantization method to address these problems. HAWQ allows for the automatic selection of the relative quantization precision of each layer, based on the layer's Hessian spectrum. Moreover, HAWQ provides a deterministic fine-tuning order for quantizing layers, based on second-order information. We show the results of our method on Cifar-10 using ResNet20, and on ImageNet using Inception-V3, ResNet50 and SqueezeNext models. Comparing HAWQ with state-of-the-art shows that we can achieve similar/better accuracy with $8\times$ activation compression ratio on ResNet20, as compared to DNAS~\cite{wu2018mixed}, and up to $1\%$ higher accuracy with up to $14\%$ smaller models on ResNet50 and Inception-V3, compared to recently proposed methods of RVQuant~\cite{park2018value} and HAQ~\cite{wang2018haq}. Furthermore, we show that we can quantize SqueezeNext to just 1MB model size while achieving above $68\%$ top1 accuracy on ImageNet.

JumpReLU: A Retrofit Defense Strategy for Adversarial Attacks

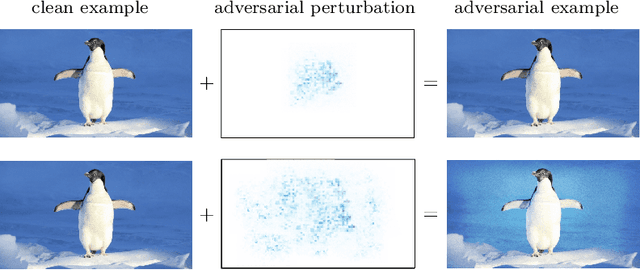
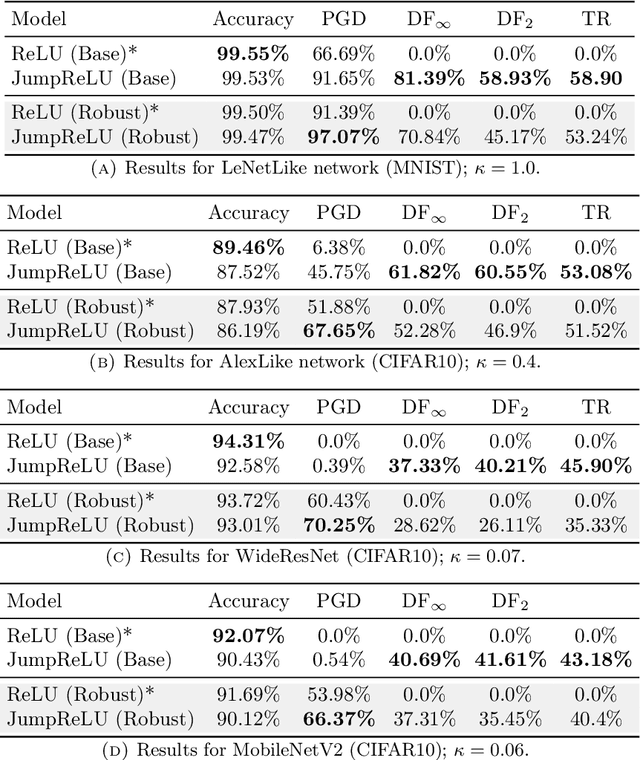
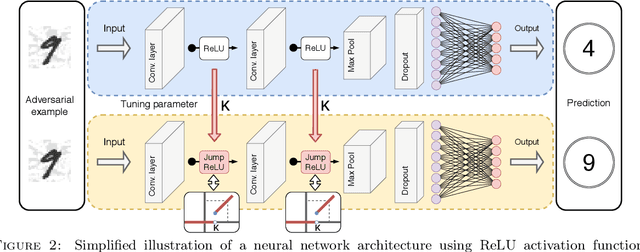
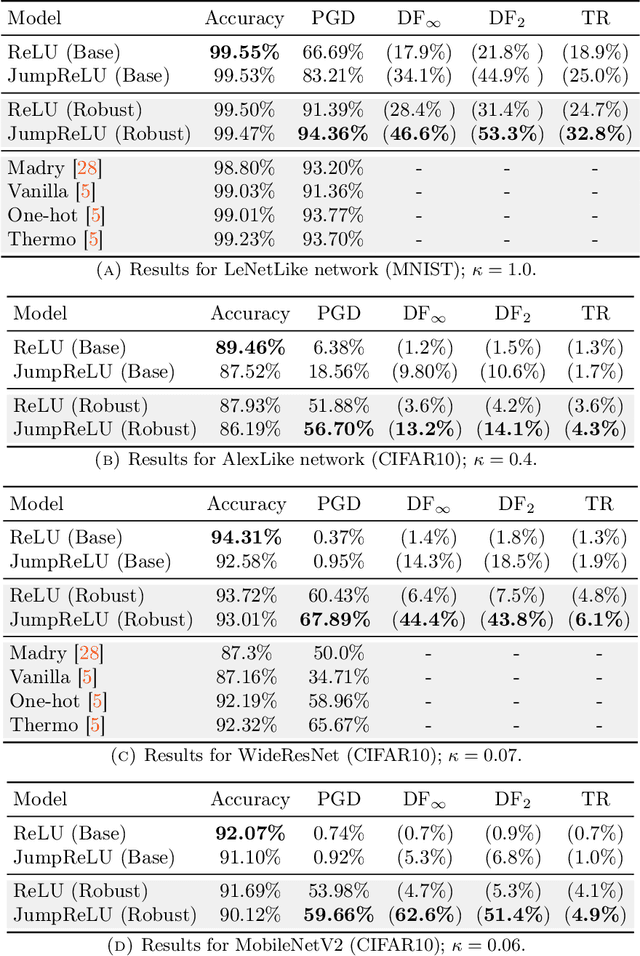
It has been demonstrated that very simple attacks can fool highly-sophisticated neural network architectures. In particular, so-called adversarial examples, constructed from perturbations of input data that are small or imperceptible to humans but lead to different predictions, may lead to an enormous risk in certain critical applications. In light of this, there has been a great deal of work on developing adversarial training strategies to improve model robustness. These training strategies are very expensive, in both human and computational time. To complement these approaches, we propose a very simple and inexpensive strategy which can be used to ``retrofit'' a previously-trained network to improve its resilience to adversarial attacks. More concretely, we propose a new activation function---the JumpReLU---which, when used in place of a ReLU in an already-trained model, leads to a trade-off between predictive accuracy and robustness. This trade-off is controlled by the jump size, a hyper-parameter which can be tuned during the validation stage. Our empirical results demonstrate that this increases model robustness, protecting against adversarial attacks with substantially increased levels of perturbations. This is accomplished simply by retrofitting existing networks with our JumpReLU activation function, without the need for retraining the model. Additionally, we demonstrate that adversarially trained (robust) models can greatly benefit from retrofitting.

Inefficiency of K-FAC for Large Batch Size Training

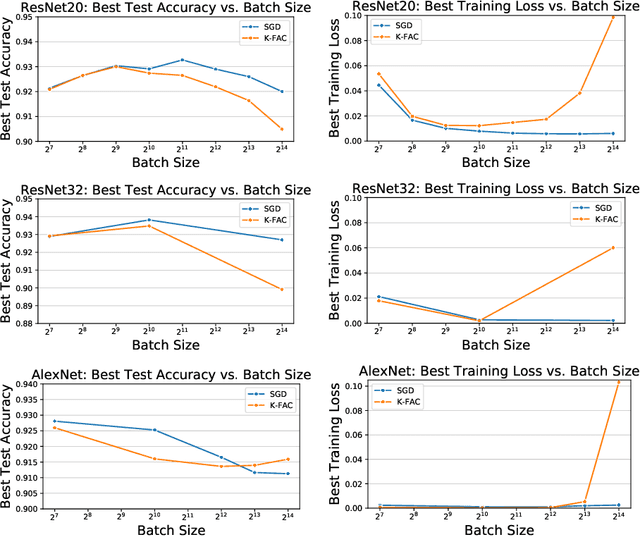
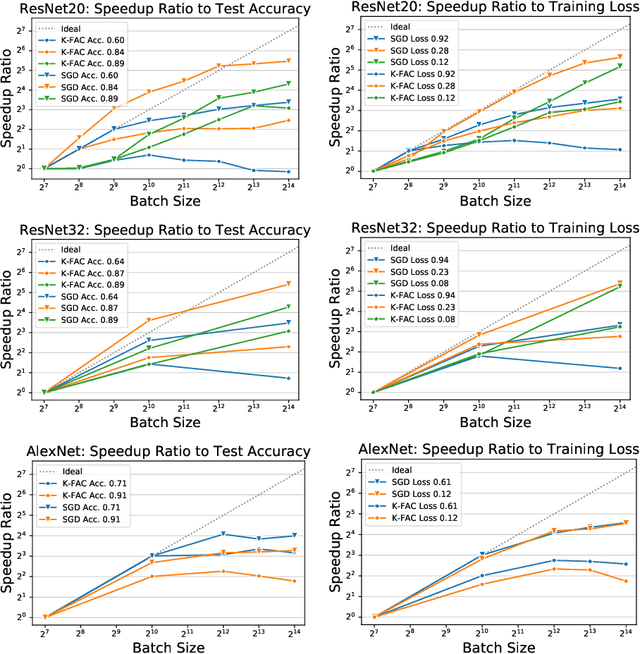
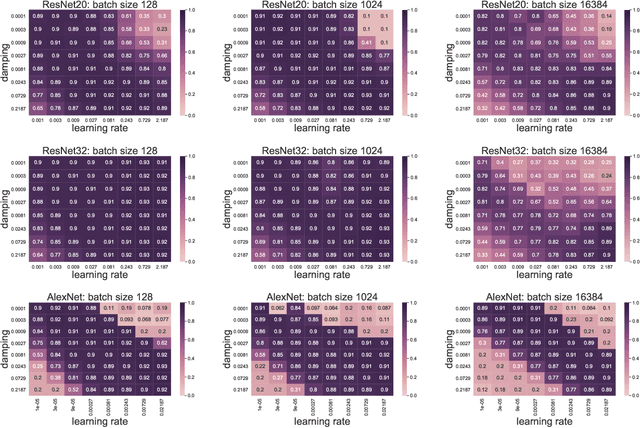
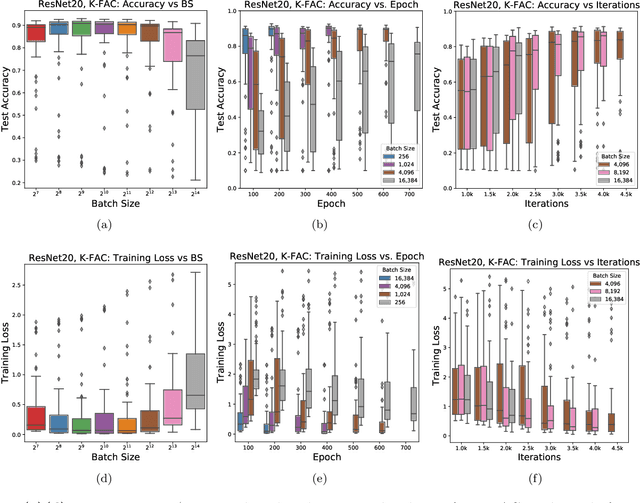
In stochastic optimization, large batch training can leverage parallel resources to produce faster wall-clock training times per epoch. However, for both training loss and testing error, recent results analyzing large batch Stochastic Gradient Descent (SGD) have found sharp diminishing returns beyond a certain critical batch size. In the hopes of addressing this, the Kronecker-Factored Approximate Curvature (\mbox{K-FAC}) method has been hypothesized to allow for greater scalability to large batch sizes for non-convex machine learning problems, as well as greater robustness to variation in hyperparameters. Here, we perform a detailed empirical analysis of these two hypotheses, evaluating performance in terms of both wall-clock time and aggregate computational cost. Our main results are twofold: first, we find that \mbox{K-FAC} does not exhibit improved large-batch scalability behavior, as compared to SGD; and second, we find that \mbox{K-FAC}, in addition to requiring more hyperparameters to tune, suffers from the same hyperparameter sensitivity patterns as SGD. We discuss extensive results using residual networks on \mbox{CIFAR-10}, as well as more general implications of our findings.

Shallow Learning for Fluid Flow Reconstruction with Limited Sensors and Limited Data

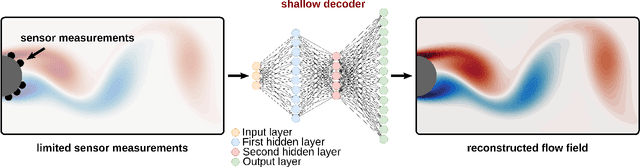
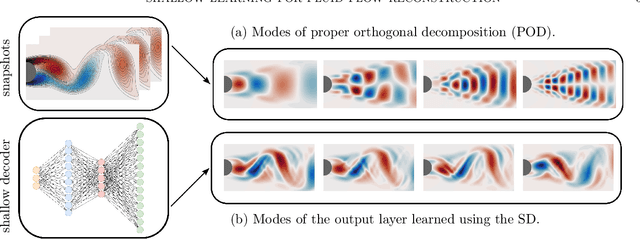
In many applications, it is important to reconstruct a fluid flow field, or some other high-dimensional state, from limited measurements and limited data. In this work, we propose a shallow neural network-based learning methodology for such fluid flow reconstruction. Our approach learns an end-to-end mapping between the sensor measurements and the high-dimensional fluid flow field, without any heavy preprocessing on the raw data. No prior knowledge is assumed to be available, and the estimation method is purely data-driven. We demonstrate the performance on three examples in fluid mechanics and oceanography, showing that this modern data-driven approach outperforms traditional modal approximation techniques which are commonly used for flow reconstruction. Not only does the proposed method show superior performance characteristics, it can also produce a comparable level of performance with traditional methods in the area, using significantly fewer sensors. Thus, the mathematical architecture is ideal for emerging global monitoring technologies where measurement data are often limited.

Trust Region Based Adversarial Attack on Neural Networks

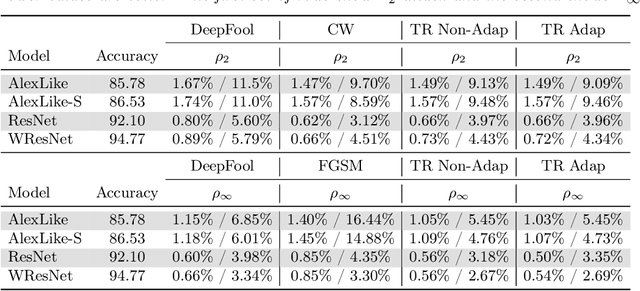
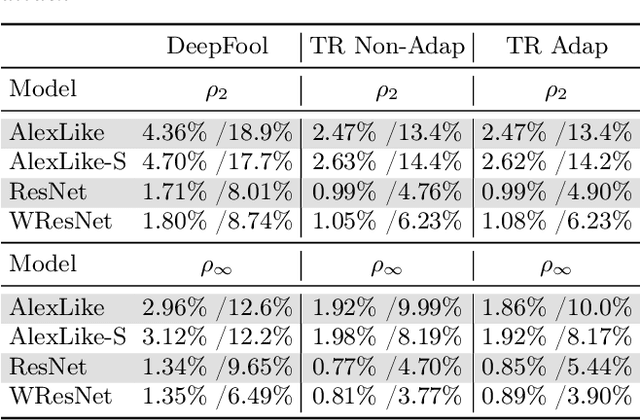
Deep Neural Networks are quite vulnerable to adversarial perturbations. Current state-of-the-art adversarial attack methods typically require very time consuming hyper-parameter tuning, or require many iterations to solve an optimization based adversarial attack. To address this problem, we present a new family of trust region based adversarial attacks, with the goal of computing adversarial perturbations efficiently. We propose several attacks based on variants of the trust region optimization method. We test the proposed methods on Cifar-10 and ImageNet datasets using several different models including AlexNet, ResNet-50, VGG-16, and DenseNet-121 models. Our methods achieve comparable results with the Carlini-Wagner (CW) attack, but with significant speed up of up to $37\times$, for the VGG-16 model on a Titan Xp GPU. For the case of ResNet-50 on ImageNet, we can bring down its classification accuracy to less than 0.1\% with at most $1.5\%$ relative $L_\infty$ (or $L_2$) perturbation requiring only $1.02$ seconds as compared to $27.04$ seconds for the CW attack. We have open sourced our method which can be accessed at [1].

Parameter Re-Initialization through Cyclical Batch Size Schedules

Optimal parameter initialization remains a crucial problem for neural network training. A poor weight initialization may take longer to train and/or converge to sub-optimal solutions. Here, we propose a method of weight re-initialization by repeated annealing and injection of noise in the training process. We implement this through a cyclical batch size schedule motivated by a Bayesian perspective of neural network training. We evaluate our methods through extensive experiments on tasks in language modeling, natural language inference, and image classification. We demonstrate the ability of our method to improve language modeling performance by up to 7.91 perplexity and reduce training iterations by up to $61\%$, in addition to its flexibility in enabling snapshot ensembling and use with adversarial training.